Rivero L.Encyclopedia of database technologies and applications.2006

Sergio Greco

DEIS Università della Calabria, Italy

Cristina Sirangelo

DEIS Università della Calabria, Italy

IrinaTrubitsyna

DEIS Università della Calabria, Italy

EsterZumpano

DEIS Università della Calabria, Italy

INTRODUCTION

The objective of this article is to investigate the problems related to the extensional integration of information sources. In particular, we propose an approach for managing inconsistent databases, that is, databases violating integrity constraints. The problem of dealing with inconsistent information has recently assumed additional relevance as it plays a key role in all the areas in which duplicate information or conflicting information is likely to occur (Agarwal et al., 1995; Arenas, Bertossi & Chomicki, 1999; Bry, 1997; Dung, 1996; Lin & Mendelzon, 1999; Subrahmanian, 1994).

As known, the presence of inconsistent data can be resolved by repairing the database, that is, by providing a computational mechanism that ensures obtaining consistent “scenarios” of the information or by consistently answering queries posed on an inconsistent set of data.

Example 1

Consider the following database schema consisting of the single relation Teaches (Name, Faculty, Course) with the functional dependency Name → Faculty. Assume to have three different sources for the relation Teaches containing, respectively, the tuples Teaches(john, science, databases), Teaches(john, engineering, algorithms), and Teaches(john, science, operating_systems). The three different source relations satisfy the functional dependencies, but from their integration, we derive the inconsistent relation D= {(john, engineering, algorithms), (john, science, operating_systems), (john, science,databases)}.

The integrated relation D can be repaired by applying a minimal set of update operations. In particular, it admits two repairs: R1 obtained by deleting the tuple (john, engineering, algorithms) and R2 obtained by deleting

the two tuples (john, science, databases) and (john, science, operating_systems).

In the presence of an alternative set of repairs, it is natural to allow user expressing preferences. In particular, methods for ranking and returning the preferred information is an increasingly key goal in AI applications ranging from information filtering and extraction to user profiling. The importance of this issue is reflected by an extensive number of proposals allowing the specification of preferences (Brewka & Eiter, 1999; Delgrande & Schaub, 2000; Gelfond & Son, 1997; Sakama & Inoue, 2000). This article is a contribution in this direction as it aims at filtering out the preferred repairs in the presence of preferences. For instance, if in the above example, preferred repairs are those minimizing the number of deletion and insertion of tuples, then the repair R1 is preferred to the repair R2.

In this article, we consider preferences among repairs and possible answers by introducing a partial order among them on the base of some preference criteria. More specifically, preferences are expressed by considering polynomial functions applied to repairs and returning real numbers. The goodness of a repair is measured by estimating how much it violates the desiderata conditions, and a repair is preferred if it minimizes the value of the polynomial function used to express the preference criteria.

Note that, while integrity constraints can be considered as a query which must always be true after a modification of the database, the conditions expressed by the evaluation function can be considered as a set of desiderata which are satisfied if possible by a generic repair. The goodness of a repair is measured by estimating how much the updates to be performed on the inconsistent database respect the preference criteria or, in other words, how much the repaired database violates them.

The main contribution of this work consists in the proposal of a logic approach for querying and repairing inconsistent databases that extend previous works (Greco,

Preferred Repairs for Inconsistent Databases

Greco & Zumpano, 2001; Greco & Zumpano, 2000) by allowing to express and manage preference criteria. The approach here proposed allows to express reliability on the information sources and is also suitable for expressing decision and optimization problems. The introduction of preference criteria strongly reduces the number of feasible repairs and answers; for special classes of constraints and functions, it gives a unique repair and answer.

BACKGROUND

A database D has associated schema DS = (RS,IC) which defines the intentional properties of D: RS denotes the set of relation schemas whereas IC contains the set of integrity constraints. Integrity constraints express semantic information over data, that is, relationships that must hold among data in the theory. Generally, integrity constraints represent the interaction among data and define properties which are supposed to be explicitly satisfied by all instances over a given database schema. Therefore, they are mainly used to validate database transactions.

Definition 1

A full (or universal) integrity constraint is a formula of the first order predicate calculus of the form:

( X) [ B1 ... Bn ϕ A1 ... Am ψ1 ... ψk ]

where A1, ..., Am, B1, ..., Bn are base positive literals, ϕ, ψ1,

..., ψk are built-in literals, X denotes the list of all variables appearing in B1,...,Bn and it is supposed that variables appearing in A1,..., Am, ϕ, ψ1, ..., ψk also appear in B1,...,Bn.

In the definition above, the conjunction B1 ... Bnϕ is called the body and the disjunction A1 ... Am ψ1 ... ψk the head of the integrity constraint. Moreover, an integrity constraint is said to be positive if no negated literals occur in it (classical definitions of integrity constraints only consider positive nondisjunctive constraints, called embedded dependencies (Kanellakis, 1991).

Often, we shall write our constraints in a different format by moving literals from the head to the body and vice versa.

PREFERRED REPAIRS FOR INCONSISTENT DATABASES

In this section, we introduce a polynomial function, through which, expressing preferences criteria. The function introduces a partial order among repairs to allow the evaluation of the goodness of a repair for an inconsistent

database. Moreover, we define preferred repairs as fea-

sible repairs that are minimal with respect to the partial P order.

Let us first recall the formal definition of consistent database and repair.

Definition 2

Given a database schema DS = (Rs,IC) we say that IC is consistent if there exists a database instance D over DS such that D |= IC. Moreover, we say that a database instance D over DS is consistent if D |=IC, that is, if all integrity constraints in IC are satisfied by D, otherwise it is inconsistent.

Intuitively, a repair for a (possibly inconsistent) database D is a minimal consistent set of insert and delete operations which makes D consistent, whereas a consistent answer for a query consists of two sets containing, respectively, the maximal set of true and undefined atoms which match the query goal; atoms which are neither true nor undefined can be assumed to be false.

More formally: see definition 3.

Definition 3

Given a database schema DS = <Rs,IC> and a database D over DS a repair for D is a pair of sets of atoms (R+,R-) such that 1) R+∩ R-= , 2) D R+- R- |= IC and 3) there is no pair (S+, S-) ≠ (R+, R-) such that R+ S+, R- S- and D S+- S- |= IC. The database D R+ - R- will be called the repaired database.

Thus, repaired databases are consistent databases which are derived from the source database by means of a minimal (under total semantics) set of insertion and deletion of tuples. Given a repair R for D, R+ denotes the set of tuples which will be added to the database, whereas R-ð denotes the set of tuples of D which will be canceled. In the following, for a given repair R and a database D, R(D) = D R+-R- denotes the application of R to D.

Moreover, given a database schema DS, we denote with D the set of all possible database instances over DS.

Definition 4

Given a (possibly inconsistent) database D over a fixed schema DS and a polynomial function f: (D,D) x D → . A repair R1 is preferable to a repair R2, w.r.t. the function f, written R1 <<f R2, if f(R1,D) ≤ f(R2,D).

A repair R for D is said to be preferred w.r.t. the function f if there is no repair R’ for D such that R’ <<f R. A repaired

database D’= D R+ - R- is said to be a preferred database if R = (R+ , R-) is a preferred repair.

The above function f will be called (repair) evaluation function as it is used to evaluate a repair R with respect to a database D. A preferred database minimizes the value of the evaluation function f applied to the source database and repairs.

Observe that, in the above definition, D denotes the domain of all possible database instances whereas (D, D) denotes the domain of all possible database updates. This means that the evaluation function f can be used to measure any possible modification of the input databases and not only to measure repairs, that is, modification which makes the database consistent. In the following, for the sake of simplicity, we only consider functions which minimize the cardinality of a set.

Example 2

Consider the database D = { Teaches(t1,c1), Teaches(t2,c2) Faculty(t1,fac1),Faculty(t2,fac1),Course(c1,fac1), Course(c2,fac2) and the integrity constraint

(P,C,F) [Teaches(P,C) , Faculty(P,F) Course(C,F) ]

Let R be a repair for the database D, possible evaluation functions are:

f1(R,D) = |R+| computing the number of inserted atoms, f2(R,D) = |R-| computing the number of deleted atoms, f3(R,D) = |R-| + |R+| computing the number of deleted and inserted atoms.

As seen in Example 1, there are three repairs for D:

R1 = ( , {Teaches(t2,c2)}),

R2 = ( , {Faculty(t2,fac1)}), and

R3 = ({Course(c2,fac1)}, ).

With respect to the above evaluation functions, we have the following relations:

R1 <<f1 R3 and R2 <<f1 R3

R3 <<f2 R1 and R3 <<f2 R2

Thus, considering the minimization of the above evaluation functions, we have that under the function f2, R3 is the unique preferred repair; under the function f1, we have two preferred repairs: R1 and R2; and under the function f3, all repairs are preferred.

Given a database D, a set of integrity constraints IC and an evaluation function f, we denote with R(D,IC,f) the set

Preferred Repairs for Inconsistent Databases

of preferred repairs for D. In the above example R (D,IC,f1) = {R1, R2 }, whereas R (D,IC,f2) = {R3 }. Moreover, we denote with f0 any constant evaluation function (e.g., f0(R,D) = 0, the function returning the value 0). R (D,IC,f0) denotes the set of all feasible repairs for D as no preference is introduced.

Rewriting into Disjunctive

Queries (Greco-Zumpano)

In Greco and Zumpano (2000), a general framework for computing repairs and consistent answers over inconsistent databases with universally quantified variables was proposed. The technique is based on the rewriting of constraints into extended disjunctive rules with two different forms of negation (negation as failure and classical negation). The disjunctive program can be used for two different purposes: compute repairs for the database and produce consistent answers, that is, a maximal set of atoms which do not violate the constraints. The technique is sound and complete (each stable model defines a repair, and each repair is derived from a stable model) and more general than techniques previously proposed.

More specifically, the technique is based on the generation of an extended disjunctive program LP derived from the set of integrity constraints. The repairs for the database can be generated from the stable models of LP whereas the computation of the consistent answers of a query (g,P) can be derived by considering the stable models of the program P LP over the database D.

Let c be a universally quantified constraint of the form

X [ B1 ... Bk not Bk+1 ... not Bn φ B0 ]

then, dj(c) denotes the extended disjunctive rule

←B’1 ... ←B’k B’k+1 ... B’n B’0 ← (B1 B’1), …, (Bk B’k), (not Bk+1 ←B’k+1), …, (not Bn ←B’n), φ , (not B0 ←B’0),

where B’i denotes the atom derived from Bi, by replacing the predicate symbol p with the new symbol pd if Bi is a base atom; otherwise, it is equal to false. Let IC be a set of universally quantified integrity constraints, then

DP(IC) = { dj(c) | c IC} whereas LP(IC) is the set of standard disjunctive rules derived from DP(IC) by rewriting the body disjunctions.

Clearly, given a database D and a set of constraints IC, LP(IC)D denotes the program derived from the union of the rules LP(IC) with the facts in D whereas SM(LP(IC)D) denotes the set of stable models of LP(IC)D

Preferred Repairs for Inconsistent Databases

and every stable model is consistent since it cannot contain two atoms of the form A and ←A. The following example shows how constraints are rewritten.

Example 3

Consider the following integrity constraints:

X [ p(X) not s(X) q(X) ] X [ q(X) r(X) ]

and the database D containing the facts p(a), p(b), s(a), and q(a).

The derived generalized extended disjunctive program is defined as follows:

←pd(X) sd(X) qd(X) ← (p(X) pd(X)) (not s(X)

← sd(X)) (not q(X) ← qd(X)).

←qd(X) rd(X) ← (q(X) qd(X)) (not r(X) ←rd(X)).

The above rules can now be rewritten in standard form. Let P be the corresponding extended disjunctive Datalog program. The computation of the program PD gives the following stable models:

M1 = D { ←pd(b), ←qd(a) }, M2 = D { ←pd(b), rd(a) }, M3 = D { ←qd(a), sd(b) }, M4 = D { rd(a), sd(b) },

M5 = D { qd(b), ←qd(a), rd(b) } and M6 = D { qd(b), rd(a), rd(b) }.

A (generalized) extended disjunctive Datalog program can be simplified by eliminating from the body rules all literals whose predicate symbols are derived and do not appear in the head of any rule (these literals cannot be true). As mentioned before, the rewriting of constraints into disjunctive rules is useful for both (1) making the database consistent through the insertion and deletion of tuples and (2) computing consistent answers leaving the database inconsistent.

Computing Database Repairs

Every stable model can be used to define a possible repair for the database by interpreting new derived atoms (denoted by the subscript “d”) as insertions and deletions of tuples. Thus, if a stable model M contains two atoms Øðpd(t) (derived atom) and p(t) (base atom), we deduce that the atom p(t) violates some constraints, and therefore, it must be deleted. Analogously, if M contains the derived atoms pd(t) and does not contain p(t) (i.e., p(t) is not in the database), we deduce that the atom p(t) should be inserted in the database. We now formalize the definition of repaired database.

Given a database schema DS = (Rs,IC) and a database

D over DS, let M be a stable model of LP(IC)D ,then, a repair P for D is a pair:

R(M) = ( {p(t) | pd (t) M p(t) D}, (p(t) | ← pd (t) M pd(t) D} ).

Given a database schema DS = (Rs,IC) and a database D over DS, a repair for D is a pair of sets of atoms (R+, R-) such that 1) R+∩ R-= , 2) D R+- R- |= IC, and 3) there is no pair (S+, S-) ≠ (R+, R-) such that S+ R+, S- R- and D S+ - S- |= IC. The database D R+ - R- will be called the repaired database.

Thus, repaired databases are consistent databases which are derived from the source database by means of a minimal set of insertion and deletion of tuples. Given a repair R for D, R+ denotes the set of tuples which will be added to the database whereas R- denotes the set of tuples of D which will be canceled. In the following, for a given repair R and a database D, R(D) = D R+ - R- denotes the application of R to D.

The technique is sound and complete:

•(Soundness) for every stable model M of LP(IC)D, R(M), there is a repair for D;

•(Completeness) for every database repair S for D,

there exists a stable model M for LP(IC)D such that

S = R(M).

FUTURE TRENDS

As a future trend, an interesting topic consists of investigating the specification of more flexible and powerful forms of preferences, that is, dynamic preferences that appear within the logic program and need to be determined “on the fly”.

CONCLUSION

In this article, we have proposed a logic programmingbased framework for managing possibly inconsistent databases. The main contribution of this work consists in the definition of a logic approach for repairing inconsistent databases that extends previous works by also considering techniques to express and manage preferences. The goodness of a repair is measured by estimating how much it violates the desiderata conditions and a repair is preferred if it minimizes the value of the polynomial function used to express the preference criteria. A further important characteristic related to the introduction of preference criteria is the reduction of feasible repairs and

answers, which lead, for special cases of constraints, to unique repair and answer.

REFERENCES

Abiteboul, S., Hull, R., & Vianu, V. (1995). Foundations of databases. Addison-Wesley.

Agrawal, S., Keller, A.M., Wiederhold, G., & Saraswat, K. (1995). Flexible relation: An approach for integrating data from multiple, possibly inconsistent databases. Proceedings of the IEEE International Conference on Data Engineering (pp. 495-504).

Arenas, M., Bertossi, L., & Chomicki, J. (1999). Consistent query answers in inconsistent databases. Proceedings of the International Conference on Principles of Database Systems (pp. 68-79).

Brewka, G., & Eiter, T. (1999). Preferred answer sets for extended logic programs. Artificial Intelligence, 109(1- 2),297-356.

Bry, F. (1997). Query answering in information system with integrity constraints. Proceedings of the IFIP WG 11.5 Working Conference on Integrity and Control in Information Systems.

Delgrande, J.P., & Schaub, T. (2000). Expressing preferences in default logic. Artificial Intelligence, 123(1-2), 41-87.

Dung, P.M. (1996). Integrating data from possibly inconsistent databases. Proceedings of the International Conference on Cooperative Information Systems (pp. 58-65).

Eiter, T., Gottlob, G., & Mannila, H. (1997). Disjunctive datalog. ACM Transactions on Database Systems, 22(3), 364-418.

Gelfond, M., & Lifschitz, V. (1991). Classical negation in logic programs and disjunctive databases. New Generation Computing, 3(4), 365-386.

Gelfond, M., & Son, T.C. (1997). Reasoning with prioritized defaults. LPKR (pp. 164-223).

Grant, J., & Subrahmanian, V.S. (1995). Reasoning in inconsistent knowledge bases. IEEE Transaction on Knowledge and Data Engineering, 7(1), 177-189.

Greco, G., Greco, S., & Zumpano, E. (2001). A logic programming approach to the integration, repairing and querying of inconsistent databases. Proceedings of the International Conference on Logic Programming.

Preferred Repairs for Inconsistent Databases

Greco, G., Sirangelo C., Trubitsyna I., & Zumpano, E. (2003). Preferred repairs for inconsistent databases. Proceedings of the International Conference on Database Engineering and Applications Symposium.

Greco, S., & Zumpano, E. (2000). Querying inconsistent databases. Proceedings of the International Conference on Logic Programming and Automated Reasoning (pp. 308-325).

Greco, S., & Saccà, D. (1990). Negative logic programs.

Proceedings of the North American Conference on Logic Programming (pp. 480-497).

Lin, J., & Mendelzon, A.O. (1999). Knowledge base merging by majority. In R. Pareschi & B. Fronhoefer (Eds.),

Dynamic worlds: From the frame problem to knowledge management. Kluwer.

Minker, J. (1982). On indefinite data bases and the closed world assumption. Proceedings of the 6th Conference on Automated Deduction (pp. 292-308).

Sakama, C., & Inoue, K. (2000). Priorized logic programming and its application to commonsense reasoning.

Artificial Intelligence, 123(1-2), 185-222.

Subrahmanian, V.S. (1994). Amalgamating knowledge bases. Proceedings of the ACM ToDS, 19(2), 291-331.

Ullman, J.K. (2000). Information integration using logical views. 239(2), 189-210.

KEY TERMS

Consistent Answer: A set of tuples, derived from the database, satisfying all integrity constraints.

Consistent Database: A database satisfying a set of integrity constraints.

Data Integration: A process providing a uniform integrated access to multiple heterogeneous information sources.

Disjunctive Datalog Program: A set of rules of the form:

A1 … Ak ← B1, ..., Bm, not Bm+1, …,not Bn, k+m+n>0

where A1,…, Ak, B1,…, Bn are atoms of the form p(t1,..., th), p is a predicate symbol of arity h and the terms t1,..., th are constants or variables.

Reda Alhajj

University of Calgary, Canada

Faruk Polat

Middle East Technical University, Turkey

INTRODUCTION

Users may derive new classes by defining views1 based on the current database contents. Some virtual classes are classified as brothers of existing classes, and others are either superclasses or subclasses of existing base and virtual classes. A base class is defined directly by the user using class definition constructs. A virtual class is classified as a brother of another class if it is derived from the latter class via a selection. To have a homogeneous system, virtual classes must be treated as first-class citizens in an object-oriented model.

In this article, we handle reusability maximization by investigating the proper location of a derived class in the hierarchy by adjusting the list of superclasses and the set of subclasses for a given class to increase inheritance instead of duplication. Our aim is to maximize inherited, and minimize locally defined characteristics by adjusting the list of superclasses to include classes that maximize inherited and minimize locally defined characteristics.

Depending on the specification of their superclasses and subclasses during query evaluation, virtual classes may be classified into four groups: (1) classes for which both superclasses and subclasses are specified; (2) classes for which only superclasses are specified; (3) classes for which only subclasses are specified; and (4) classes for which neither superclasses nor subclasses are specified. Reusability decreases from the first group to the fourth group. Two algorithms are presented to achieve the target of maximizing reusability when possible.

BACKGROUND

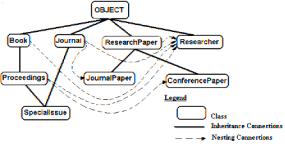
Shown in Figure 1 is a class hierarchy that will be referenced frequently in the article where illustrating examples are necessary. Given next is the basic terminology necessary to understand the rest of this article.

Figure 1. An example class hierarchy

1.Pd(c): set of classes used in deriving class c; Pd is empty for base classes because they are user defined.

2.Cp(c): list of direct superclasses of class c.

3.Cb(c): set of direct subclasses of class c.

4.Linstances(c): set of object identifiers of objects added directly to class c.

5.Winstances(c): set of object identities of objects in class c and its direct and indirect subclasses.

6.Wattributes(c): set of attributes that determine the state of objects in Linstances(c). It includes inherited and locally defined attributes.

7.Lattributes(c): set of additional attributes locally defined in class c, that is, Lattributes(c) Wattributes(c).

8.Wbehavior(c): set of methods common to all objects in class c. It includes both inherited methods and locally defined methods.

9.Lbehavior(c): set of additional methods locally defined in class c, that is, Lbehavior(c) Wbehavior(c). For every virtual class c, Lbehavior(c) includes a method, called FindObjects(), which implements the query expression that decides on objects in Winstances(c).

10.m(c, f, r): the header of method m such that, m Lbehavior(c), f is the list of domains for formal parameters, and r is the domain of the result.

Example 1: [Base classes] All the classes shown in Figure 1 are base classes. Next are the characteristics of some of them, where B, J, P, SI, RP, R, JP, and CP stand for Book, Journal, Proceedings, SpecialIssue, ResearchPaper, Researcher, JournalPaper, and ConferencePaper, respectively:

Cp(B)=[OBJECT] Cb(B)={P} Pd(B)=φ

Lattributes(B)={title:String, author:[R], year:Date, subject:String, publisher:String}

Lbehavior(B)={title(), title(t), author(), author(p), year(), year(y),

Lattributes(P)={location:String, chairperson:R, committee:{R},

Lattributes(J)={title:String, EditorInChief:R, EditorialBoard:{R}, subject:String, publisher:String, contents:[JP]}

Lbehavior(J)={title(), title(t), EditorInChief(), EditorInChief(e), EditorialBoard(), EditorialBoard(p), subject(), subject(s), pub-

lisher(), publisher(p), contents(), contents(c)}

Example 2: [Brother class] Given DBJournals as a brother of class J with: Pd(DBJournals)={J}. By definition, DBJournals has the following characteristics:

C p ( D B J o u r n a l s ) = [ ] C b ( D B J o u r n a l s ) = { } Lattributes(DBJournals)={}Lbehavior(DBJournals)={FindObjects()}

L i n s t a n c e s ( D B J o u r n a l s ) = { }

Being its brother, DBJournals shares the characteristics of class J, and Winstances(DBJournals) is determined by invoking the method FindObjects(DBJournals).

Example 3: [Virtual classes] Consider the following characteristics of some example derived classes.

PP: (PrintedPublications) includes all books and journals.

Pd(PP)={B,J} Cp(PP)=[OBJECT] Cb(PP)={B, J}

Winstances(PP)=Winstances(B) 7 Winstances(J) Linstances(PP)={}

Lattributes(PP)={title:String, subject:String, publisher:String}

Lbehavior(PP)={title(), title(t), subject(), subject(s), publisher(), publisher(p), FindObjects()}

NP: (NewProceedings) includes only some characteristics from class P.

NRP: includes all attributes of class RP and the name of the major researcher who contributed to the paper.

Pd(NRP)={RP} Cp(NRP)=[RP] Cb(NRP)={}

Linstances(NRP)={}Lattributes(NRP)={name:String}

Winstances(NRP)=Winstances(RP) Lbehavior(NRP)={name(),name(s), FindObjects()}

MAIN THRUST

Locally defined characteristics of class c include

Lattributes(c) and Lbehavior(c). The inherited characteristics of class c are (Wattributes(c)–Lattributes(c) and (Wbehavior(c)– Lbehavior(c)). In this section, we present two algorithms to investigate adjusting for a given class: (1) its list of

superclasses and (2) its set of subclasses. The first is necessary for classes in the third group, and the second is suitable for classes in the second group. However, both algorithms are required for classes in the fourth group.

Algorithm 1 investigates the possibility of maximizing reusability by adding some existing classes to Cp(c) or by pushing class c into the list of superclasses of some existing classes. We employ the following heuristic; having Cb(c) not empty helps in limiting our search to the direct and indirect superclasses of every class in Cb(c). Otherwise, we have to consider and investigate all classes in the hierarchy, which is the general case when Cb(c) is empty. For each class cb Cb(c), Definition 1 is used to find the inheritance list of class cb, denoted IL(cb), that includes all its direct and indirect superclasses. For the other case of having Cb(c) empty, the class hierarchy must be traced top-down and left to right in order to include all the classes present in the hierarchy inside IL(c). Algorithm 1 checks for the possibility of including inside Cp(c) any of the classes in IL(cb), and the list of superclasses of the considered class is adjusted accordingly.

Definition 1: [Inheritance List] Given any class c, IL(c) is defined using:

1.For every cp Cp(c), cp IL(c);

2.For every c’ IL(c), classes in Cp(c’) are placed at the head of IL(c);

3.Nothing else belongs to IL(c).

Example 4: [Inheritance List] IL(SI)=[B,J,P] and

IL(P)=[B].

Algorithm 1: [Maximize Inherited Characteristics]

Input: class c and Cb(c)

Output: The class hierarchy adjusted to maximize reusability.

Let K be a list of classes, which is initially empty; For every class cb Cb(c) do

Find IL(cb) by Definition 1; For every cj IL(cb) do

if (Winstances(c) Winstances(cj)) and (Wbehavior(cj) Wbehavior(c))

Cp(c)=Cp(c)–Cp(cj);

Cp(c)=Cp(c)+{cj};

For every attribute iv Lattributes(cj) do Let d1 be the underlying domain in

Lattributes(cj);

Let d2 be the underlying domain in

Lattributes(c); if d1=d2 then

Lattributes(c)=Lattributes(c)–{iv};

For every message m Lbehavior(cj) do Let m(cm,fm,rm) be the header of the

method underlying message m in

Lbehavior(cj);

Let m(cn,fn,rn) be the header of the method underlying message m in

Lbehavior(c);

if cm=cn and fm=fn and rm=rn then Execute both methods using a sample set of objects from class c;

if both methods give the same result then

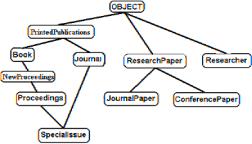
Example 5: [Pushing a class inside the hierarchy] Consider the two virtual classes PP and NP as input to Algorithm 1, which revises their characteristics to get:

Lbehavior(PP)={title(), title(t), subject(), subject(s), publisher(), publisher(p), FindObjects()}

Figure 2. The revised class hierarchy after adding PP and NP

Lattributes(NP)={location:String, chairperson:R} Lbehavior(NP)={location(), location(l), chairperson(), chairperson(p), FindObjects()}

As a result, the two virtual classes have been pushed into proper locations within the hierarchy as shown in Figure 2. Note that PP was not affected by Algorithm 1 because it was not violating reusability maximization. On the other hand, characteristics of NP have been modified, and NP has been pushed under B.

As illustrated in Example 5, Algorithm 1 is useful mainly for results of projection, as well as union and difference with non-brother2 classes as operands. These results were proved to be superclasses of the operands (Alhajj & Arkun, 1993; Alhajj & Polat, 1994). But, it is also possible to have result vc as subclass of the operand(s); for example, the result of nest is a subclass of the first operand. It is semantically desirable to make the additional properties acquired by objects in

Winstances(vc) reachable only when such objects are accessed from vc itself. Based on this, we developed a

second approach where the new properties are made accessible solely from vc.

We introduced artificial classes into the hierarchy. Every class in the hierarchy produces an artificial class. Artificial classes contain only objects, and they inherit all other class characteristics. An artificial class ac con-

tains objects that qualify to be in Linstances(c), where c is the corresponding class in the hierarchy3; that is, objects

migrate from Linstances(c) into Linstances(ac), hence, are still considered in Winstances(c). Further, given any two classes c’ and c’’ that result in artificial subclasses ac’ and ac’’,

respectively, having c’ as a subclass of c’’ leads to have ac’ as a subclass of ac’’. It is an implementation issue to make artificial classes invisible and inaccessible to the user.

Definition 2: [Artificial Class] For every class c, there is a corresponding artificial class ac such that:

1.c IL(ac), class ac is created first as a subclass of class c. Later on, as more artificial classes are created, ac may move down the hierarchy and becomes indirectly connected to class c;

2.Any object oid that qualifies to be in Linstances(c) is

added to Linstances(ac) instead. This way,

oid Linstances(ac) and Linstances(ac) Winstances(c), be-

cause c IL(ac) oid Winstances(c);

3.Given two classes c’ and c’’ such that c’ Cb(c’’), then ac’ Cb(ac’’).

Example 6: [Artificial classes] Given two classes, c’ and c’’ such that c’ Cb(c’’), it is required to introduce a new class vc’’ as subclass of c’’ such that

Winstances(c’) Winstances(vc’’) and vc’’ has more characteristics (includes more attributes and behavior) than c’.

We cannot add c’ to Cb(vc’’) as shown in Figure 3(a) because the additional characteristics of vc’’ will be seen from class c’, which is not the required target. We resolve this issue by following the artificial classes approach as shown in Figure 3(b).

From Figure 3(b), every class will continue to exist without being affected by class vc’’, which will be able to recognize all related information in the hierarchy. Notice that artificial class ac’’ is not a direct subclass of c’’. This is formalized next in Algorithm 2, where an artificial class ac is dropped from Cb(c) when ac becomes an indirect subclass of c.

Algorithm 2: [Subclass addition]

Input: Two classes c and vc such that vc is to be added to Cb(c)

Output: The adjusted class hierarchy.

3.Construct artificial class avc according to Definition 2

4.Cb(c)=Cb(c)–{ac}

To illustrate Algorithm 2, consider adding virtual class NRPs to the hierarchy shown in Figure 4, which is derived by adding artificial classes to the hierarchy shown in Figure 1. The obtained hierarchy is shown in Figure 5.

Finally, when an object oid is added to class c’, which may be either a direct or indirect subclass of class c’’, it is necessary to consider the direct virtual subclasses of c’’ in order to polish oid such that it qualifies to be in

Winstances(vc’’) for every virtual class vc’’ÎCb(c’’). This is smoothly accomplished because oid is added to

Linstances(ac’) instead of Linstances(c’). Algorithm 2 forces ac’ to be a subclass of vc’’, and this leads to having

Linstances(ac’) Winstances(vc’’). On adding oid to Linstances(ac’), it must carry all the characteristics defined for objects

of the classes found in IL(ac’), but without violating inheritance rules. Since vc’’ is in IL(ac’), oid will carry the characteristics defined for objects that qualify to be in Winstances(vc’’).

FUTURE TRENDS

The derived type is treated as a separate entity in the work of Shaw and Zdonik (1990). In Carey, DeWitt, and Vandenberg (1988) new types created during query processing do not participate in inheritance in any way; neither do they become part of any inheritance hierarchy. The approach of Kaul, Drosten, and Neuhold (1990) establishes only a local relationship between the derived type and the source type.

A new class in Kim (1989) is placed as a direct subclass of the root of the hierarchy. All the methods and attributes required to be in this new class have to be replicated from