
Rivero L.Encyclopedia of database technologies and applications.2006
.pdf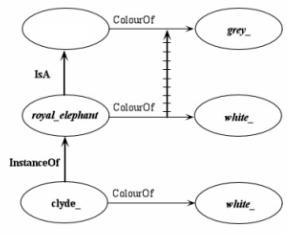
ColourOf or, in other terms, that the property ColourOf of elephant_ must not be considered as a systematically inheritable property. An at least implicit differentiation between “overriding properties” and “non-overriding properties” is then introduced in the set of properties (attributes, slots, etc.) that characterize a given concept: For elephant_ and all its instances and specific terms, we can say, e.g., that FormOfTheTrunk is a non-overriding property, given that its associated value will always be cylinder_; ColourOf will be, on the contrary, overriding. Figure 2 visualizes the situation described in the three assertions above; the crossed line (“cancel link”) indicates that the value associated with the overriding property ColourOf has been actually changed, passing from elephant_ to royal_elephant. Note that, in most of the systems dealing concretely with ontologies, the cancel link is not explicitly implemented, and the overriding can be systematically executed.
In a well-known article, R.J. Brachman (1985) warns about the logical inconveniences linked with the introduction of an unlimited possibility of overriding. Under the complete overriding hypothesis, the values associated with the different properties of the concepts, and the properties themselves, must now be interpreted simply as “defaults,” that is, always possible to modify. Brachman gives, in particular, a very extreme example linked with the possibility that the properties can be overridden, leaving, on the contrary, the associated values unchanged: A giraffe_ is then considered as an elephant_ where the value cylinder_ associated with the property TrunkOf of elephant_ is unchanged, but the property itself has been overridden, and it is now called NeckOf for giraffe_ (Brachman, 1985, pp. 85-86). It is evident that it becomes now unfeasible to make use of inheritance as a “definitional” principle, i.e., to make use of the internal structure of the different concepts—linked with the presence of
Figure 2. Overriding (defeasible inheritance)
|
|
|
elephant_ |
|
ColourOf |
|
|
|
|
|
||||
|
|
|
|
|
|
|
_grey |
|||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
IsA |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ColourOf |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
royal_elephant |
|
|
|
|
white_ |
|
||||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
InstanceOf |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
clyde_ |
|
|
|
|
|
|
|
white_ |
|||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ontologies and Their Practical Implementation
particular properties and values—to determine, e.g., whether a given concept A is more general or more specific than B. This leads, inter alia, to the impossibility of determining automatically the position of a new concept in the inheritance network and to conclude that a hypothetical elephant_with_three_legs or a yellow_elephant (this last is an unfortunate elephant suffering from hepatitis) is still an elephant_. The benefits associated with the use of the inheritance hierarchies seem then close to vanishing; without endorsing completely such catastrophic conclusions, it appears clearly that an uncontrolled amount of overriding can introduce some really serious coherence problems.
Given, however, that dealing with exceptions is an evident necessity in the knowledge representation domain, artificial intelligence (AI) researchers have tried to avoid the danger of an uncontrolled use of overriding techniques by using some form of non-classical logic— in particular, Reiter’s (1980) default logic —to provide a formal semantics for inheritance hierarchies with defaults. Very briefly, a “default theory” is a pair (D, W) where D is a set of “default rules” (seen as a sort of inference rules) concerning normally the properties of the concepts, like “Typically, elephants have four legs,” and W is a set of “hard facts,” like “All elephants are mammals” (or “Margaret Mitchell wrote Gone With the Wind”). Formally, W is a set of first-order formulae, while a typical default rule of D can be denoted as:
α(x1,..., xn) :β(x1,..., xn)
|
; |
(2) |
|
γ(x1,..., xn) |
|||
|
|
where α, band γ are again first-order formulae whose free variables are among x1, …, xn. The notation ω(xi), used for the first-order formulae of (2), is here an abridged logicallike notation representing in general both (IsAxiω) (InstanceOf ω) and (HasProperty xiω). Informally, a rule like (2) means then: for any individuals x1, …, xn, if α(x1, …, xn) is inferable and if b(x1, …, xn) can be consistently assumed, then infer γ(x1, …, xn). For the previous example concerning royal elephants, (2) becomes:
elephant _(x) : gray _(x) ¬royal _ elephant(x)
|
. (3) |
|
gray _(x) |
||
|
From the informal definition above, it can be seen that, if we assume simply that (InstanceOf clyde_ elephant_), we can affirm that (ColourOf clyde_ gray_) and ¬ (InstanceOf clyde_ royal_elephant) are both consistent with this assumption; hence, (ColourOf clyde_ gray_) can be inferred. In a more formal way, from the initial assumption elephant_(clyde_), and having veri-
440
TEAM LinG
Ontologies and Their Practical Implementation
fied that gray_(clyde_) and ¬ royal_elephant(clyde_) are consistent with the assumption, we can infer gray_(clyde_). On the other hand, if the initial assumption is now royal_elephant(clyde_), using the hard fact (IsA royal_elephant elephant_), see Figure 1, we can be reduced again to the situation of the previous example, i.e., elephant_(clyde_); in this case, however, the consistency condition b(x1, …, xn) = gray_(x)¬royal_elephant(x) is violated given the initial assumption royal_elephant(clyde_) that “blocks” the default rule, preventing then the derivation of gray_ (clyde_).
The inheritance hierarchy of Figure 1 is a “tree,” i.e., each node (concept) has only one node immediately above it (its “parent node”), from which it can inherit the properties. In this case, the mode of transmission of the properties is called “single inheritance.” For taxonomies, this is the normal situation; in real-world ontologies, however, a concept can have multiple parents and can inherit properties along multiple paths; e.g., the dog_ of Figure 1 can also be seen as a pet_, inheriting then all the properties of the ancestors of pet_, pertaining maybe to a branch private_property of the global inheritance hierarchy. This phenomenon is called “multiple inheritance”; the inheritance hierarchy becomes now a “tangled hierarchy” (a DAG) as opposed to a tree—a partially ordered set (poset) from a mathematical point of view. Multiple inheritance contributes strongly to the simplification of the inheritance hierarchies by eliminating the need for the duplication of the concepts and of the corresponding instances that would be required to reduce the hierarchy to a simple tree; possible examples of duplicated concepts could be dog_as_valuable_object and dog_as_carnivore_mammal. The use of the multiple inheritance approach can, however, give rise to conflicts when a concept inherits the same property from two (or more) different ancestors, and these properties have different values. This problem and the possible solutions are illustrated, e.g., in Bertino et al., 2001, pp. 142-144).
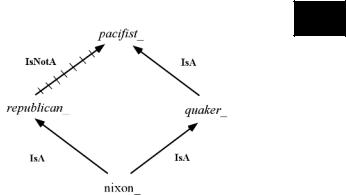
When defeasible inheritance (materialized by the presence of cancel links) and multiple inheritance combine, we can be confronted with very tricky situations like the notorious “Nixon diamond”; see Figure 3. In this version of the diamond, the most frequently used, we admit that it is possible to have an individual, nixon_, as a common instance of two different concepts, republican_ and quaker_. Several inheritance-based systems do not allow this possibility; postulating, however, the presence of an intermediate concept like republican_having_ quaker_convictions, which specializes both republican_ and quaker_ and to which we could attach the nixon_ instance, would not change the essence of the problem. If we ask now: “Is Nixon a pacifist or not?” we are in trouble, given that, as a Quaker, Nixon is (typically) a pacifist, but, as a Republican, Nixon is (typically) not a
Figure 3. Nixon diamond
O
pacifist. A reasoner dealing with this situation must then choose between two possible attitudes. According to a “skeptical” attitude, it will refuse to draw conclusions in ambiguous situations, and, therefore, it will emit no opinion as to whether Nixon is or is not a pacifist. According to a “credulous” attitude, the reasoner will try to deduce as much as possible, generating then all the possible “extensions” of the ambiguous situation. In the Nixon diamond case, it will then generate both the solutions, pacifist_ and ¬ pacifist_.
This problem (and similar ones) has given rise to a flood of theoretical work, which cannot be described here; see, e.g., Touretzky (1986) and Bertino et al. (2001, pp. 144147) for a synthesis.
Definitions of Concepts as Frames
Until now, we have considered the concepts as they were characterized solely by (i) a conceptual label (a symbolic name) and (ii) their hierarchical relationships with all the other concepts symbolized by the use of the IsA links. We will see now how it could be possible to associate to any concept a “structure” (a “frame”) reflecting the knowledge human beings have about (i) the intrinsic properties of these concepts and (ii) the network of relationships, other than the hierarchical one, the concepts have with each other. As already stated above, we are now totally in the “ontological” domain, and this sort of frame-based ontology can be equated to the well-known “semantic networks”; see Lehmann (1992).
Basically, a “frame” is a set of properties, with associated classes of admitted values, that is linked to the nodes representing the concepts. Introducing a frame corresponds then to establishing a new sort of relationship between the concept Ci to be defined and some of the other concepts of the ontology. The relationship concerns the fact that the concepts C1, C2 … Cn used in the frame defining Ci indicate now the “class of fillers” (spe-
441
TEAM LinG

cific concepts or instances) that can be associated with the “slots” of this frame, the slots denoting the main properties (attributes, qualities, etc.) of Ci. There is normally no fixed number of slots, nor a particular order imposed on them; slots can be accessed by their names.
To show how it can possible to introduce a formal description of the relationships between Ci and concepts C1, C2 … Cn, let us suppose that concept C1 (e.g., home_address) is endowed with a property R (e.g., HasNecessarily) linking it with a concept C2 (e.g., postal_code). This situation can be formalized as:
x(C1(x) → y(C2(y) R(x, y))); |
(4) |
meaning then, according to our example, that every home address is endowed with the property of having a postal code. As already stated in the previous section, properties can be systematically inherited along an inheritance hierarchy only under the “strict inheritance” hypothesis; instances inherit from the father concept.
The properties of Ci—i.e., the relationships between Ci and some other concepts of the ontology that define the classes of fillers for the slots of the frame associated with Ci—can pertain to several, different classes. According, e.g., to the classification used for the strictly “ontological” part of the NKRL language (see the next section and Zarri, 1997), these properties (slots) can be grouped in three different classes: “relations,” “attributes,” and “procedures” (see Table 1, where OID [object identifier] stands for the symbolic name of the particular concept or individual [instance of a concept]).
The slots of the “relation” type are used to represent mutual kinds of relationships between a concept or individual and other concepts or individuals. They can be “standard” or “user defined.” In Table 1, eight of them (“standard”) are shown; they are: IsA and the inverse HasSpecialization, InstanceOf and the inverse HasInstance, MemberOf (HasMember), and PartOf
Table 1. Types of slots in a frame
{ OID
[ Relation |
(IsA | |
InstanceOf |
: |
||
|
HasSpecialization |
| HasInstance : |
|||
|
MemberOf |
| |
HasMember : |
||
|
PartOf |
| |
HasPart |
:) |
|
|
(UserDefined1 |
: |
|
||
|
… |
|
|
|
|
Attribute |
UserDefinedn |
: ) |
|
||
(Attribute1 |
: |
|
|
||
|
… |
|
|
|
|
Procedure |
Attributen |
: ) |
|
|
|
(Procedure1 : |
|
|
|||
|
… |
|
|
|
|
Proceduren : ) ]}
Ontologies and Their Practical Implementation
(HasPart). Some of the formal properties of the relation properties are described in Table 2.
An important point concerns the fact that, because of the definitions of “concept” and “instance” given in the previous section and of the properties of IsA, InstanceOf, PartOf, and MemberOf illustrated in Table 2, a concept or an individual (instance) cannot make use of the totality of the eight “relations” introduced above. More exactly:
•The relation IsA and the inverse HasSpecialization are reserved to concepts.
•HasInstance can only be associated with a concept; InstanceOf with an individual (i.e., the concepts and their instances, the individuals, are linked by the InstanceOf and HasInstance relations).
•Moreover, MemberOf (HasMember) and PartOf (HasPart) can only be used to link concepts with concepts or instances with instances, but not concepts with instances; see also Winston, Chaffin, and Herrmann (1987).
The characteristic properties of a concept/individual are specifically represented by the slots of the “attribute” type. For example, for a concept like tax_, possible attributes are TypeOfFiscalSystem, CategoryOfTax, Territoriality, TypeOfTaxPayer, TaxationModalities, etc. The restrictions about the sets of legal fillers for the “attribute” slots can be expressed using single concepts or particular combinations of concepts: e.g., an expression like “(INTERSECTION human_being (UNION doctor_ lawyer_) (NOT.ONE.OF fred_))” can be used to designate a class of fillers that are men, can be doctors or lawyers, but cannot be Fred.
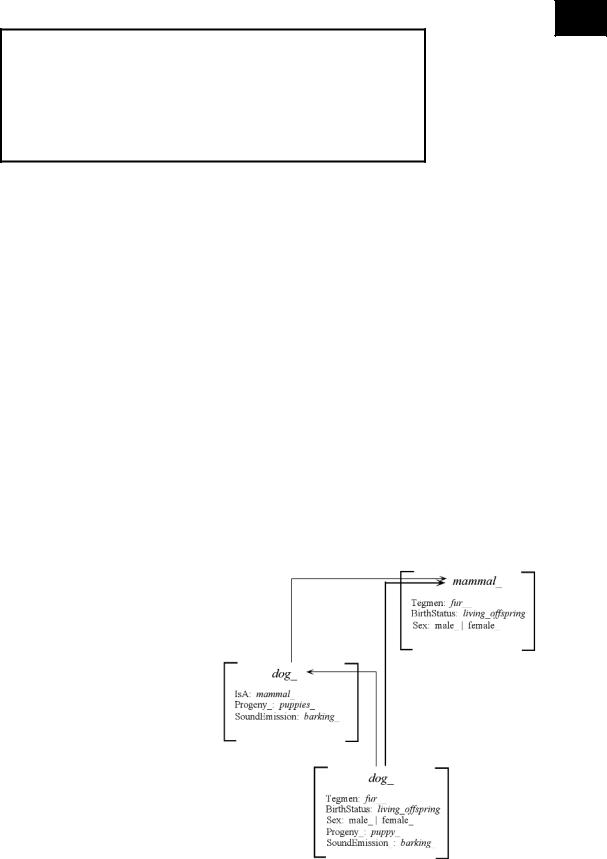
Figure 4 (an “ontology”) reproduces a fragment of Figure 1 (a “taxonomy”), where the concepts are now associated with their (highly schematized) defining frames; note that the two fillers (non-sortal concepts) male_ / female_ could also have been replaced by their subsuming concept sex_. This figure makes explicit what “inheritance of properties/attributes” means: Supposing that the frame for mammal_ is already defined and supposing now to tell the system that the concept dog_ is characterized by the two specific properties Progeny and SoundEmission, what the frame dog_ really includes is represented in the lower part of Figure 4.
The function assigned to slots of the “procedure” type is that of providing, in case, alternative inference and representation schemes in addition to the inheritancebased methods and representations. They normally supply various ways of attaching to frames “procedural” information, expressed using ordinary programming languages like Java, LISP, or C. A more detailed discussion in this context and an example can be found, e.g., in Bertino et al. (2001, pp. 152-154).
442
TEAM LinG
Ontologies and Their Practical Implementation
Table 2. Some properties of IsA, Instance Of, PartOf, and MemberOf
O
(IsA A B) (IsA B A) ↔ A ≡ B
(IsA A B) (IsA B C) → (IsA A C) (IsA is a partial order relationship) (IsA A B) (IsA A C) → D (IsA B D) (IsA C D)
(PartOf A B) → ← (PartOf B A)
(PartOf A B) (PartOf B C) → (PartOf A C) (IsA A B) (PartOf B C) → (PartOf A C) (IsA A B) (PartOf A C) → (PartOf B C) (IsA B C) (A PartOf A C) → (PartOf A B)
(IsA A B) (MemberOf B C) → (MemberOf A C)
(InstanceOf C A) (IsA A B) → (InstanceOf C B)
(PartOf C D) (InstanceOf C A) (?InstanceOf D B) → (PartOf A B) (PartOf A B) (InstanceOf D B) → C (InstanceOf C A) (PartOf C D)
Even if, under the influence of the Semantic Web work (see the companion article in this encyclopedia “Using Semantic Web Tools for Ontologies Construction”), the “classic” frame paradigm as expounded above is moving towards more formalized and logic-based types of representation, nevertheless, this paradigm still constitutes the foundation for the setup of a large majority of knowledge bases all over the world. Often, therefore, a knowledge base is nothing more than a “big” ontology formed of concepts/individuals represented under the form of frames. Unfortunately, frames suffer from congenital problems of unpredictability linked mainly (but not exclusively) with the arbitrariness in the choice of the slots. This arbitrariness is only partially obviated in some of the tools devoted to facilitate the setup of large knowledge bases by the use of meta-structures intended to describe in a precise way the computational behavior of a given slot—and therefore to give, in a certain way, also a sort of “definition” of the slot. A well-known approach in this context consists in adding “facets” to the slots, where a facet represents an annotation describing some characteristics of the slots, like type restrictions on the values of the slot (value-type facets) and specifications of the exact number of possible values that the slot may take on (cardinality facets).
To circumvent these unpredictability problems and enforce interoperability in the construction of knowledge bases—by allowing, e.g., the reuse of existing knowledge components or the import/export of ontologies—an Open Knowledge Base Connectivity (OKBC) protocol was developed in the late ’90s; see, e.g., Chaudhri, Farquhar, Fikes, Karp, and Rice, (1998) and Table 3. OKBC is an application programming interface (API) specifying the operations that can be used to access a knowledge base by an application program; to do this, OKBC must make some assumptions about the knowledge representations used in the accessible knowledge bases and thus define, eventually, a “knowledge model,” to which such knowledge bases must conform. The OKBC knowledge model is very general, in order to include the representational
features supported by a majority of frame-based knowledge systems, and concerns general directions about the representation of constants, frames, slots, facets, etc. It allows frame-based systems to define their own behavior for many aspects of the knowledge model, e.g., with respect to the definition of the default values for the slots.
The most well-known OKBC-compatible tool for the setup of knowledge bases making use of the frame model is Protégé-2000, developed for many years at the Medical Informatics Laboratory of Stanford University (in California, USA); see, e.g., Noy, Fergerson, and Musen (2000) and Noy et al. (2001). Protégé-2000 represents today a sort of standard in the ontological domain. A Protégé ontology consists of “classes,” i.e., the concepts proper to a given application domain; “slots,” describing the properties or the attributes of the classes/concepts; “facets,” describing the properties of the slots; and “axioms,” used
Figure 4. A simple example explaining the inheritance of properties/attributes
443
TEAM LinG
Ontologies and Their Practical Implementation
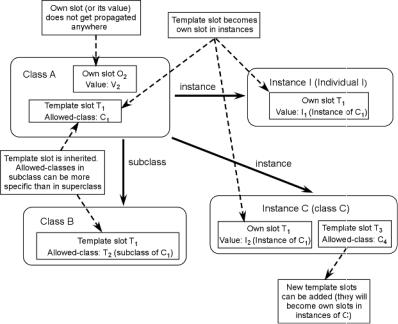
Figure 5. Propagation of template and own slots in Protégé-2000
to represent additional constraints. A Protégé “knowledge base” includes the ontology and the different “individuals” obtained as instances of classes when some specific values have been defined for the slots.
Definition of classes is a standard one: If a class B is a subclass of a class A, then every instance of B is also an instance of A. Multiple inheritance is admitted. A more controversial decision concerns the fact of admitting that both individuals and classes themselves can be instances of classes; see also Figure 5. In this way, Protégé can introduce “metaclasses” as classes whose instances are themselves classes. Every class (concept) has then a dual identity; it is a “subclass” of another class (its “superclass”) in the normal class hierarchy, and it is at the same time an “instance” of another class (its “metaclass”). As a class defines a sort of “compelling mold” for its instances, the metaclass defines a compelling mold for the associated classes, describing, e.g., which “own slots” (see below) these last can have and the constraints for the values of these slots. Metaclasses can be user-defined, allowing then the users to customize the Protégé-2000 tool according to the requirements of their domain and tasks.
The most important contribution of OKBC and Protégé to the development of “modern” frame systems concerns, however, the definition of the slots. Slots in Protégé and OKBC are frames in themselves; more importantly, they are first-class objects that are defined independently of
any class, i.e., independently from the requirements of any particular concept. Bearing in mind that slots represent properties or attributes of a concept, it is now evident that properties like Age or Name can be used to describe the characteristics of both (among many other things) the concepts author_ and manuscript_. These slots will then be “attached,” when necessary, to author_, manuscript_, and many other possible concepts (classes). When a slot is “attached” to a class, it can take a “value.” In Protégé (and OKBC), the constraints that specify the allowed slot values are expressed through “facets.”
Slots can be attached to classes or instances in two ways, i.e., as “template slots” or as “own slots.” Own slots can be attached to both classes and instances; they define “local” properties of classes and instances, and, when attached to a class, they cannot be inherited by its subclasses and instances. Template slots can be attached only to classes; they can be inherited by the subclasses, and, when inherited by the instances of a class, they become own slots for these instances—analogously, own slots associated with classes were, originally, template slots of their specific metaclasses. The whole mechanism of the “attachment” is summarized in Figure 5, adapted from Figure 2 of Noy et al. (2000); see this last paper for more details on the attachment mechanism and for concrete examples. Table 3, derived from the same paper, summarizes the differences between the OKBC and Protégé-2000 knowledge models.
444
TEAM LinG

Ontologies and Their Practical Implementation
Table 3. Comparison between the OKBC (first column) and Protégé-2000 (second column) knowledge models
O
1 |
A frame (class or instance) can be an |
A frame (class or instance) can be an |
|
instance of multiple classes. |
instance of only one class. |
2 |
A frame (class or instance) has not to |
A frame (class or instance) is always a |
|
be necessarily an instance of a class. |
an instance of a class. |
3 |
An own slot can be attached directly |
An own slot attached to a frame is |
|
to any frame (class or instance). |
always derived from a template slot. |
4 |
Classes, slots, facets, and individuals |
Every class, slot, facet, and individual |
|
must not be necessarily frames. |
is necessarily a frame. |
5 |
A frame can be at the same time a class, |
A frame is either a class, or a slot, or |
|
a slot, a facet, and an individual. |
a facet, or an individual. |
FUTURE TRENDS: BEYOND “TRADITIONAL” ONTOLOGIES
A big amount of important, “economically relevant” information is buried into “narrative” information resources: This is true, e.g., for most of the corporate knowledge documents (memos, policy statements, reports, minutes, etc.), news stories, normative and legal texts, medical records, many intelligence messages, etc., as well as, in general, for a huge fraction of the information stored on the Web. In these narrative “documents,” the main part of the information content consists in the description of “events” that relate the real or intended behavior of some “actors” (characters, personages, etc.)—the term “event” is taken here in its more general meaning, covering also strictly related notions like fact, action, state, situation, etc. These actors try to attain a specific result, experience particular situations, manipulate some (concrete or abstract) materials, send or receive messages, buy, sell, deliver, etc. Note that, in these narrative documents, the actors or personages are not necessarily human beings; we can have narrative documents concerning, e.g., the vicissitudes in the journey of a nuclear submarine (the “actor,” “subject,” or “personage”) or the various avatars in the life of a commercial product. Note also that, even if a large amount of narrative documents concerns natural language (NL) texts, this is not necessarily true. A photo representing a situation that, verbalized, could be expressed as “Three nice girls are lying on the beach” is not of course an NL text, yet it is still a narrative document.
Because of the ubiquity of these “narrative” resources, being able to represent in a general, accurate, and effective way their semantic content—i.e., their key “mean- ing”—is then both conceptually relevant and economically important.
“Traditional” ontologies are not very suitable to deal with this problem. Their form of hierarchical organization is, in fact, largely sufficient to provide a static, a priori definition of the class/concepts and of their properties. This is no more true when we consider the dynamic
behavior of the concepts, i.e., we want to describe their mutual relationships when they take part in some concrete action, situation, etc. (“events”), in particular, when those “connectivity phenomena,” like causality, goal, indirect speech, coordination and subordination, etc., that link together “elementary events” must be taken into account. It is very likely, in fact, that, dealing with the sale of a company, the global information to represent is something like: “Company X has sold its subsidiary Y to Z because the profits of Y have fallen dangerously these last years due to a lack of investments,” or that, dealing with the relationships between companies in the biotechnology domain, “X made a milestone payment to Y because they decided to pursue an in vivo evaluation of the candidate compound identified by X.” It is now easy to imagine the awkward proliferation of totally ad hoc slots/ properties that, sticking to a strict frame context, it would be necessary to introduce in order to approximate the connectivity phenomena in the above examples.
NKRL (Narrative Knowledge Representation Language; Zarri, 2003) innovates then with respect to the usual ontology paradigm by associating with the traditional ontologies of concepts, an “ontology of events,” i.e., a new sort of hierarchical organization where the nodes correspond to n-ary structures called “templates.”
Instead of using the traditional object (class, concept) – attribute – value organization, templates are generated from the combination of quadruples, connecting together the symbolic name of the template, a predicate, and the arguments of the predicate introduced by named relations, the roles. The quadruples have in common the “name” and “predicate” components. If we denote then with Li the generic symbolic label identifying a given template, with Pj the predicate used in the template, with Rk the generic role, and with ak the corresponding argument, the NKRL core data structure for templates has the following general format:
(Li (Pj (R1 a1) (R2 a2) … (Rn an))) |
(5) |
See the example in Table 4. Predicates pertain to the set {BEHAVE, EXIST, EXPERIENCE, MOVE, OWN, PRO-
445
TEAM LinG

DUCE, RECEIVE}, and roles to the set {SUBJ(ect), OBJ(ect),SOURCE,BEN(e)F(iciary),MODAL(ity),TOPIC, CONTEXT}. An argument of the predicate can consist of a simple “concept” (according to the traditional “ontological” meaning of this word) or of a structured association (“expansion”) of several concepts.
Templates are included in turn in an inheritance hierarchy, HTemp(lates), which implements the new “ontology of events”; they represent then formally generic classes of elementary events like “move a physical object,” “be present in a place,” “produce a service,” “send/ receive a message,” “build up an Internet site,” etc. When a particular event pertaining to one of these general classes must be represented, the corresponding template is “instantiated” to produce what, in the NKRL’s jargon, is called a “predicative occurrence.”
To represent then a narrative event like “British Telecom will offer its customers a pay-as-you-go (payg) Internet service in autumn 1998,” we must select firstly in the HTemp hierarchy the template corresponding to “supply a service to someone,” represented in the upper part of Table 4. This template is a specialization (see the “father” code) of the particular MOVE template of HTemp corresponding to “transfer of resources to someone.” In a template, the arguments of the predicate (the ak terms in (5)) are represented by variables with associated con- straints—which are expressed as concepts or combinations of concepts, i.e., using the terms of the NKRL standard “ontology of concepts” (HClass, “hierarchy of classes”). The constituents (as Source in Table 4) included in square brackets are optional. When deriving a predicative occurrence (an instance of a template) like c1 in Table 4, the role fillers in this occurrence must conform
Ontologies and Their Practical Implementation
to the constraints of the father template. For example, in occurrence c1, british_telecom is an individual instance of the concept company_, which is, in turn, a specialization of human_being_or_social_body; payg_internet_service is a specialization of service_, a specific term of social_activity, etc. The meaning of the expression “BENF (SPECIF customer_ british_telecom)” in c1 is self-evident: The beneficiaries (role BENF) of the service are the customers of—SPECIF(ication)—British Telecom. In the occurrences, the two operators date-1 and date-2 materialize the temporal interval normally associated with narrative events; see Zarri (1998).
About 180 templates are permanently inserted into Htemp; this ontology of events corresponds then to a sort of “catalogue” of narrative formal structures that, moreover, are very easy to “customize” in order to derive the new templates that could be needed for a particular application. This approach is particularly advantageous for practical applications, and it implies, in particular, that: (i) a system builder does not have to create himself the structural knowledge needed to describe the events proper to a (sufficiently) large class of narrative documents; and (ii) it becomes easier to secure the reproduction or the sharing of previous results.
The basic NKRL knowledge representation tools are complemented by more complex mechanisms intended to represent, among other things, those “connectivity phenomena” already mentioned that, in a sequence of statements, cause the global meaning to go beyond the simple addition of the information conveyed by each single statement. This is obtained making use of second-order structures created through reification of the predicative occurrences’ conceptual labels. For example, the “bind-
Table 4. Deriving a predicative occurrance from a template
name: Move:TransferOfService father: Move:TransferToSomeone position: 4.24
NL description: 'Transfer or Supply a Service to Someone'
MOVE |
SUBJ |
|
var1: [var2] |
|
|
OBJ |
|
var3 |
|
|
[SOURCE |
var4: [var5]] |
||
|
BENF |
|
var6: [var7] |
|
|
[MODAL |
var8] |
|
|
|
[TOPIC |
var9] |
|
|
|
[CONTEXT |
var10] |
|
|
|
{[modulators]} |
|
||
var1 |
= |
<human_being_or_social_body> |
||
var3 |
= |
<service_> |
|
|
var4 |
= |
<human_being_or_social_body> |
||
var6 |
= |
<human_being_or_social_body> |
||
var8 |
= |
<process_> |
<sector_specific_activity> |
|
var9 |
= |
<sortal_concept> |
||
var10 |
= |
<situation_> |
|
|
var2, var5, var7 = <geographical_location> |
||||
c1) |
MOVE |
SUBJ |
british_telecom |
|
|
|
OBJ |
payg_internet_service |
|
|
|
BENF |
(SPECIF customer_ british_telecom) |
|
|
|
date-1: after-1-september-1998 |
||
|
|
date-2: |
|
|
446
TEAM LinG

Ontologies and Their Practical Implementation
ing occurrences” are NKRL structures consisting of lists of symbolic labels (ci) of predicative occurrences; the lists are differentiated making use of specific binding operators like GOAL and CAUSE. If, in Table 4, we would state that “British Telecom intends to offer to its customers a pay-as-you-go (payg) Internet service…,” we should introduce an additional predicative occurrence simplified here as: c2) BEHAVE SUBJ british_telecom, and meaning that “at the date (date-1) associated with c2, it can be noticed that British Telecom is acting in some way.” We will then add a binding occurrence c3 of the form: c3) (GOAL c2 c1). The meaning of c3 is that: “the activity described in c4 is focalized towards (GOAL) the realization of c1,” where c1 is represented in Table 4.
Reasoning ranges from the direct questioning of an NKRL knowledge base making use of “search patterns” (the formal NKRL equivalents of natural language queries) that try to unify the predicative occurrences of the base, to high-level inference procedures employing a complex inference engine. For example, the “transformation rules” try to “adapt,” from a semantic point of view, the original query/queries (search patterns) that failed to the real contents of the system knowledge base. The principle employed consists in using rules to automatically “transform” the original query (i.e., the original search pattern) into one or more different queries (search patterns) that are not strictly “equivalent” but only “semantically close” to the original one. In this way, an original query posed, e.g., in terms of “searching for evidence of having lived in a given country” will be replied in terms of “searching for evidence of an original school/ university diploma delivered in that country.” “Hypothesis rules” allow building up “reasonable” answers according to a number of predefined reasoning schemata, e.g., “causal” schemata. For example, after having directly retrieved information like: “Pharmacopeia, an USA biotechnology company, has received $64,000,000 from the German company Schering in connection with an R&D activity,” we could be able to automatically construct a sort of “causal explanation” of this information by retrieving in the knowledge base information like: (i) “Pharmacopeia and Schering have signed an agreement concerning the production by Pharmacopeia of a new compound,” and (ii) “In the framework of the agreement previously mentioned, Pharmacopeia has actually produced the new compound.”
Other systems exist that, being based on knowledge representation schemata richer than those of the traditional ontologies, can assure, as in NKRL, a level of inferencing neatly more “appealing,” powerful, and concise than that supplied by “traditional” ontological systems. Conceptual graphs (CGs) are a representation system developed by John Sowa (1999) and derived from
early work in the Semantic networks domain that makes
use of a graph-based notation for representing “con- O cepts” (and “concept referents”) and “conceptual relations.” Like NKRL, CGs can be used to represent in a formal way narrative events like “A pretty lady is dancing gracefully” and more complex, second-order construc-
tions like contexts, wishes, and beliefs. CYC (see Lenat, Guha, Pittman, Pratt, & Shepherd, 1990) concerns one of the most controversial endeavors in the history of artificial intelligence. Started in the early ’80s as a MCC (Microelectronics and Computer Technology Corp., Texas, USA) project, it ended about 15 years later with the setup of an enormous knowledge base containing about a million hand-entered “logical assertions,” including both simple statements of facts and rules about what conclusions can be inferred if certain statements of facts are satisfied. The “upper level” of the ontology that structures the CYC knowledge base is now freely accessible on the Web; see http://www.cyc.com/cyc/opencyc. A detailed analysis of the origins, developments, and motivations of the CYC project can be found in Bertino et al. (2001, pp. 275-316).
CONCLUSION
From the beginning of the ’70s, artificial intelligence (AI) and databases have shared some common interests. The origin of this convergence can be traced back, in a very concise way, to the lack of semantic support that characterized the “traditional” DBs, while early AI systems were limited in their capacity to supply and maintain large amounts of factual data. The so-called intelligent database systems (IDBSs; Bertino et al., 2001) are the result of this mutual impregnation—and ontologies are now presented as the ultimate instrument for the setup of “true” IDBSs. We think that this assertion is not totally unreasonable on the condition that the word “ontology” could be understood according to its widest meaning—to include also, e.g., the dynamic behavior and the mutual relationships among concepts and not only some static, a priori definition of these concepts and of their properties. As we have seen in the previous section, this can be realized by adding, as in NKRL, “ontologies of events” to the traditional “ontologies of concepts.”
REFERENCES
Bertino, E., Catania, B., & Zarri, G. P. (2001). Intelligent database systems. London: Addison-Wesley and ACM Press.
447
TEAM LinG
Brachman, R. J. (1983). What IS-A is and isn’t: An analysis of taxonomic links in semantic networks. IEEE Computer, 16(10), 30-36.
Brachman, R. J. (1985). “I lied about the trees,” or, defaults and definitions in knowledge representation. AI Magazine, 6(3), 80-93.
Chaudhri, V. K., Farquhar, A., Fikes, R., Karp, P. D., & Rice, J. P. (1998). OKBC: A programmatic foundation for knowledge base interoperability. In Proceedings of the 1998 National Conference on Artificial Intelligence, AAAI/ 98. Cambridge, MA: MIT Press/AAAI Press.
Gruber, T. R. (1993). A translation approach to portable ontology specifications. Knowledge Acquisition, 5, 199-220.
Guarino, N., & Giaretta, P. (1995). Ontologies and knowledge bases: Towards a terminological clarification. In N.J.I. Mars (Ed.), Towards very large knowledge bases: Knowledge building & knowledge sharing. Amsterdam: IOS Press.
Lehmann, F. (Ed.). (1992). Semantic networks in artificial intelligence. Oxford, UK: Pergamon Press.
Lenat, D. B., Guha, R. V., Pittman, K., Pratt, D., & Shepherd, M. (1990) CYC: Toward programs with common sense.
Communications of the ACM, 33(8), 30-49.
Noy, N. F., Fergerson, R. W., & Musen, M. A. (2000). The knowledge model of Protégé-2000: Combining interoperability and flexibility. In R. Dieng & O. Corby, O. (Eds.), Knowledge Acquisition, Modeling, and Management: Proceedings of the European Knowledge Acquisition Conference, EKAW’2000. Berlin, Germany: SpringerVerlag.
Noy, N. F., Sintek, M., Decker, S., Crubezy, M., Fergerson, R. W., & Musen, M. A. (2001). Creating Semantic Web contents with Protégé-2000. IEEE Intelligent Systems, 16(2), 60-71.
Reiter, R. (1980). A logic for default reasoning. Artificial Intelligence, 13, 81-132.
Sowa, J. F. (1999). Knowledge representation: Logical, philosophical, and computational foundations. Pacific Grove, CA: Brooks Cole.
Touretzky, D. S. (1986). The mathematics of inheritance systems. London: Pitman.
Winston, M. E., Chaffin, R., & Herrmann, D. (1987). A taxonomy of part-whole relations. Cognitive Science, 11, 417-444.
Ontologies and Their Practical Implementation
Zarri, G. P. (1997). NKRL, a knowledge representation tool for encoding the “meaning” of complex narrative texts.
Natural Language Engineering, 3, 231-253.
Zarri, G. P. (1998). Representation of temporal knowledge in events: The formalism, and its potential for legal narratives. Information & Communications Technology Law,
7, 213-241.
Zarri, G. P. (2003). A conceptual model for representing narratives. In R. Jain, A. Abraham, C. Faucher, & van der Zwaag (Eds.), Innovations in knowledge engineering. Adelaide, South Australia, Australia: Advanced Knowledge.
KEY TERMS
Frame-Based Representation: A way of defining the “meaning” of a concept by using a set of properties (“frame”) with associated classes of admitted values— this “frame” is linked with the node representing the concept. Associating a frame with the concept ci to be defined corresponds to establishing a relationship between ci and some of the other concepts of the ontology; this relationship indicates that the concepts c1, c2 … cn used in the frame defining ci denote the “class of fillers” (specific concepts or instances) that can be associated with the “slots” (properties, attributes, qualities, etc.) of the frame for ci.
Inheritance Hierarchies: Ontologies/taxonomies are structured as hierarchies of concepts (“inheritance hierarchies”) by means of “IsA” links. A semantic interpretation of this relationship among concepts, when noted as (IsA B A), means that concept B is a specialization of the more general concept A. In other terms, A subsumes B. This assertion can be expressed in logical form as:
x (B(x) → A(x)) |
(1) |
(1) says that, e.g., if any elephant_ (B, a concept) IsA mammal_ (A, a more general concept), and if clyde_ (an instance or individual) is an elephant_, then clyde_ is also a mammal_.
IsA and InstanceOf Links: The necessary complement of IsA for the construction of well-formed hierarchies is the InstanceOf link, used to introduce the “instances” (concrete examples) of the general notions represented by the concepts. The difference between (IsA B
A) and (InstanceOf C B) can be explained by considering B as a subclass of A in the IsA case, operator “ ,” and by
448
TEAM LinG

Ontologies and Their Practical Implementation
considering C as a member of the class B in the InstanceOf case, operator “ .” The notion of instance is, however, much more controversial than that of concept. Problems about the definition of instances concern, e.g., (i) the possibility of accepting that concepts (to the exclusion of the root) could also be considered as “instances” of their generic concepts and (ii) the possibility of admitting several levels of instances, i.e., instances of an instance.
NKRL: The Narrative Knowledge Representation Language. “Classical” ontologies are largely sufficient to provide a static, a priori definition of the concepts and of their properties. This is no more true when we consider the dynamic behavior of the concepts, i.e., we want to describe their mutual relationships when they take part in some concrete action, situation, etc. (“events”). NKRL deals with this problem by adding to the usual ontology of concept an “ontology of events,” a new sort of hierarchical organization where the nodes, called “templates,” represent general classes of events like “move a physical object,” “be present in a place,” “produce a service,” “send/receive a message,” etc.
Ontologies vs. Taxonomies: In a taxonomy (and in the most simple types of ontologies), the implicit definition of a concept derives simply by the fact of being inserted in a network of specific/generic relationships
(IsA) with the other concepts of the hierarchy. In a “real” ontology, we must supply also some explicit definitions for the concepts—or at least for a majority among them. This can be obtained, e.g., by associating a “frame” (see above) with these concepts.
Open Knowledge Base Connectivity (OKBC) Protocol: A protocol aiming at enforcing interoperability in the construction of knowledge bases. The OKBC
knowledge model is very general, in order to include the representational features supported by a majority of frame- O based knowledge systems, and concerns general direc-
tions about the representation of constants, frames, slots, facets, etc. It allows frame-based systems to define their own behavior for many aspects of the knowledge model, e.g., with respect to the definition of the default values for the slots. The most well-known OKBC-compatible tool for the setup of knowledge bases making use of the frame model is Protégé-2000, developed for many years at the Medical Informatics Laboratory of Stanford University, and that represents today a sort of standard in the ontological domain.
Overriding and Multiple Inheritance: Two among the main theoretical problems that can affect the construction of well-formed inheritance hierarchies. Overriding (or “defeasible inheritance,” or “inheritance with exceptions”) consists in the possibility of admitting exceptions to the “strict inheritance” interpretation of an IsA hierarchy. Under the complete overriding hypothesis, the values associated with the different properties of the concepts, and the properties themselves, must be interpreted simply as “defaults,” that is, always possible to modify. An unlimited possibility of overriding can give rise to problems of logical incoherence; Reiter’s default logic has been proposed to provide a formal semantics for inheritance hierarchies with defaults. In a “multiple inheritance” situation, a concept can have multiple parents and can inherit properties along multiple paths. When overriding and multiple inheritance combine, we can be confronted with very tricky situations like that illustrated by the well-known “Nixon diamond.”
449
TEAM LinG
