
Joye M.Cryptographic hardware and embedded systems.2005
.pdf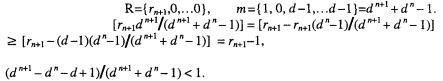
56 |
L. Hars |
There are two choices for the scaled modulus,  and
and 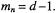 The corresponding modular reduction algorithms are denoted by S10 and S0F. In both cases
The corresponding modular reduction algorithms are denoted by S10 and S0F. In both cases  gives the estimate. Both algorithms need to store and process only the LS n digits of the scaled modulus, the processing of the MS digits can be hardwired.
gives the estimate. Both algorithms need to store and process only the LS n digits of the scaled modulus, the processing of the MS digits can be hardwired.
Algorithm S0F The initial conversion step changed the modulus, such that  and
and  The current remainder R is shifted up (logically, that is only the indexing is changed) to make it n+2 digits long, such that
The current remainder R is shifted up (logically, that is only the indexing is changed) to make it n+2 digits long, such that
Proposition:  is never too large, sometimes it is 1 too small. Proof: (similar to the proof under S10 below)
is never too large, sometimes it is 1 too small. Proof: (similar to the proof under S10 below) 
Correction steps q is often off by 1. It results in an overflow, i.e., the bit is not cleared from above the MS digit of the partial results. We have to correct them immediately (by subtracting m), otherwise the next q will be 17 bits long, and the error of the ratio estimation is doubled, so there could be a still larger overflow next.
These frequent correction steps cannot be avoided with one digit scaling. It corresponds to a division of single digits and they don’t provide good quotient estimates. The S10 algorithm below uses an extra bit, so it is better in this sense.
Algorithm S10: The initial conversion step changed the modulus, such that  and
and  The current remainder R is shifted to the left (logically, that is only the indexing is changed) to make it also n+2 digits long, such that
The current remainder R is shifted to the left (logically, that is only the indexing is changed) to make it also n+2 digits long, such that  We use signed remainders and have to handle overflows, that is, a sign and an overflow bit could temporarily precede the digits of R. The algorithm will add/subtract m to fix the overflow if it occurs.
We use signed remainders and have to handle overflows, that is, a sign and an overflow bit could temporarily precede the digits of R. The algorithm will add/subtract m to fix the overflow if it occurs.
Now there are  bits of the modulus fixed, and the signed R is providing also
bits of the modulus fixed, and the signed R is providing also  bits of information for q. With them correction steps will rarely be needed. Proposition:
bits of information for q. With them correction steps will rarely be needed. Proposition:  for
for  and
and  for R < 0 assignment gives an estimate of the quotient, which is never too small, sometimes 1 too large.
for R < 0 assignment gives an estimate of the quotient, which is never too small, sometimes 1 too large.
Proof: When  the extreme cases are:
the extreme cases are:
1. Minimum/maximum: |
and |
The true quotient is |
|
because  is integer and the subtracted term inside the integer part function is positive and less than 1:
is integer and the subtracted term inside the integer part function is positive and less than 1:
2. Maximum/minimum:  and
and 
 give
give 
These show that the estimated q is never too small.
When R is negative, the modular reduction step is done with adding q·m to R. The above calculations can be repeated with the absolute value of R. However, the estimated (negative) quotient would be sometimes 1 too small, so we increase its value by one. This is also necessary to keep q a single-digit number. 
TEAM LinG

|
|
|
|
|
Long Modular Multiplication for Cryptographic Applications |
57 |
||
Correction steps. |
Over- |
|
|
|||||
flow requiring extra cor- |
|
|
||||||
rection |
steps, |
almost |
|
|
||||
never occurs. |
Computer |
|
|
|||||
experiments showed that, |
|
|
||||||
during |
over |
10 |
million |
|
|
|||
random |
8192×8192 |
mod |
|
|
||||
8192-bit modular multi- |
|
|
||||||
plications there were only |
|
|
||||||
5 subtractive |
corrections |
|
|
|||||
step performed, no under- |
|
|
||||||
flow was detected. Dur- |
|
|
||||||
ing |
over |
random |
|
|
||||
1024×1024 mod 1024-bit |
|
|
||||||
modular |
multiplications |
|
|
|||||
there |
were 2 |
overflows |
|
|
||||
and |
no |
underflow. |
Ac- |
Fig. 11. Basic structure of the S10 modular multiplication |
||||
cordingly, the use of only |
||||||||
|
|
|||||||
software corrections does |
algorithm |
|
|
not slow down S10. |
|
The remainder is rarely longer than n +1, because at the start, there is no overflow: the MS digits of the products, even together with all the others don’t give longer than  -digit results. After a modular reduction
-digit results. After a modular reduction
if the estimated quotient q was correct, the remainder R is less than mS, that is, either or
or where the third digit is smaller than that of mS. This last case is very unlikely (less than 1/(4d) ).
where the third digit is smaller than that of mS. This last case is very unlikely (less than 1/(4d) ).
if the estimated quotient q was one too large, the remainder R changes sign. If the correct quotient q–1 would reduce R to a number of smaller magnitude than  with the third digit at most as large as that of mS, then the actual q could cause an overflow. Again, it is a very unlikely combination of events.
with the third digit at most as large as that of mS, then the actual q could cause an overflow. Again, it is a very unlikely combination of events.
Implementation. The MS 3 digits and the sign/overflow bits of the partial results can be kept in the accumulator. Because the multiplier is not used with the special MS digits of the scaled modulus, they can be manipulated together in the accumulator. Adding the next product-digit is done also in the accumulator in a single cycle.
Proposition: There is no need for longer than 50-bit accumulator.
Proof. The added product-digit could cause a carry less than n to the  digit. If there was already an overflow, this digit is 0, so there will be no further carry propagation. If the
digit. If there was already an overflow, this digit is 0, so there will be no further carry propagation. If the  digit was large, we know, the
digit was large, we know, the  digit of R was zero. These show that the MS digit of R can be –2, –1, 0, 1 — exactly what can be represented by the carry and sign, as a 2-bit 2’s complement number.
digit of R was zero. These show that the MS digit of R can be –2, –1, 0, 1 — exactly what can be represented by the carry and sign, as a 2-bit 2’s complement number. 
TEAM LinG

58 |
L. Hars |
|
|
|
Computing the scaling factor. S Let n, |
denote the length of m, A and B respec- |
|||
tively. Let us calculate |
|
for S0F, and |
for S10. With |
|
normalized |
so we get S one bit and one digit long. If the short |
|||
division estimated the long one inaccurately, we may need to add or subtract m, but at most a couple of times suffice, providing an O(n) process. Adding/subtracting m changes the MS digit by at most 1, so it gets the desired value at the end.
5.4 Montgomery Multiplication with Multiply-Accumulate Structure
We can generate the product-digits of AB from right to left and keep updating R, an n +1-digit partial remainder, initialized to 0. The final result will be also in R. When the next digit of AB has been generated with its carry (all necessary digit-products accumulated), it is added to R, followed by adding an appropriate multiple of the modulus t·m, such that the last digit is cleared:  with
with  It can be done in a single sweep over R. The result gets stored in R shifted by 1 digit to the right (suppressing the trailing 0). The new product-digit, when calculated in the next iteration, is added again to the LS position of R.
It can be done in a single sweep over R. The result gets stored in R shifted by 1 digit to the right (suppressing the trailing 0). The new product-digit, when calculated in the next iteration, is added again to the LS position of R.
Fig. 12. Montgomery multiplication with multiply-accumulate structure
Proposition after each reduction sweep (loop i) the remainder is  This fact ensures, that the intermediate results do not grow larger than n+1 digits,
This fact ensures, that the intermediate results do not grow larger than n+1 digits,
and a single final correction step is enough to reduce the result R into [0, m). If 
and any of the MS digits  k = 2, 3, 4..., then R remains always n-digit long. (The case where each but the 2 LS digits of m is d–1 is trivial to handle.)
k = 2, 3, 4..., then R remains always n-digit long. (The case where each but the 2 LS digits of m is d–1 is trivial to handle.)
Proof by induction. At start it is true. At a later iteration  is the new product-digit,
is the new product-digit,
We don’t need correction steps or processing the accumulator, so some HW costs can be saved. The final reduction step can be omitted during a calculation chain [5], since the next modular reduction produces a result  from n-digit inputs, anyway. Only the final result has to be fixed. Also, double-speed squaring can be easily done in the loop (j,k).
from n-digit inputs, anyway. Only the final result has to be fixed. Also, double-speed squaring can be easily done in the loop (j,k).
Montgomery-T (Tail Tailoring) The Montgomery reduction needs one multiplication to compute the reduction factor t. Using Quisquater’s scaling, this time to transform the LS, instead of the MS digit to a special value, we can get rid of this multiplication. The last modular reduction step is performed with the original modulus m to reduce the result below m.
TEAM LinG

Long Modular Multiplication for Cryptographic Applications |
59 |
||
If m' =1, the calculation of |
becomes trivial: |
It is the case if |
|
what we want to achieve with scaling. |
|
|
|
The first step in each modular reduction sweep, |
has to be performed |
||
even though we now the LS digit of the result (0), because the carry, the MS digit is
needed. If |
we know the result without calculation: |
|
Accordingly, we can start the loop 1 digit to the left, saving one multi- |
plication there, too. Therefore, the modular reduction step is not longer than what it was with the sorter modulus.
To make |
we multiply (scale) m with an appropriate one-digit factor S, |
|
which happens to be the familiar constant |
because |
|
|
Multiplying m with S increases its length by 1 digit, but as we |
|
have just seen, the extra trailing digit does not increase the number of digitmultiplications during modular reduction.
The modular reduction performs n–1 iterations with the modulus mS: n(n–1) digit-multiplications, and one iteration with the modulus m: n +1 digit-multiplications. We saved n–1 digit-multiplications during the modular reduction steps. The price is the need to calculate S, mS and store both m and mS.
Proof of correctness: One Montgomery reduction step calculates 
with such a k, that ensures no remainder of the division. Taking this equation modulo m, we get 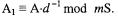 After n–1 iterations the result is
After n–1 iterations the result is 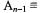
 The final step is a reduction mod m:
The final step is a reduction mod m:  In general (a mod b·c) mod c = a mod c, (for integers a, b and c), so we get
In general (a mod b·c) mod c = a mod c, (for integers a, b and c), so we get 
 or m larger than that (the result is of the same length as m). This is the result of the original Montgomery reduction.
or m larger than that (the result is of the same length as m). This is the result of the original Montgomery reduction. 
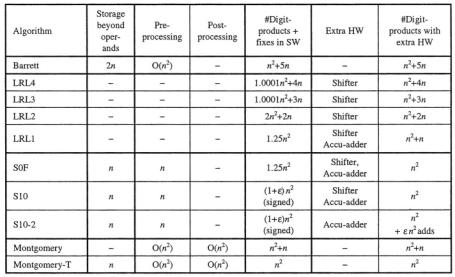
6 Summary
There is no single “best” modular multiplication algorithm, for all circumstances.
In software for general purpose microprocessors
For very long operands sub-quadratic multiplications are the best, like Karatsuba, Toom-Cook or FFFT-based methods [6]
For cryptographic applications
If memory is limited (or auxiliary data does not fit to a memory cache): LRL3 or LRL1 (dependent on the instruction timing)
If memory is of no concern: S10 or Montgomery-T (needs pre/post-process) If some HW enhancements can be designed:
If there is enough memory: S10 (simpler) Otherwise: LRL1.
The table below summarizes the running time of the modular reduction phase of our modular multiplication algorithms (without the  steps of the multiplication phase).
steps of the multiplication phase).
TEAM LinG
60 |
L. Hars |
References
1.ALTERA Literature: Stratix II Devices http://www.altera.com/literature/lit-stx2.jsp
2.P.D.Barrett, Implementing the Rivest Shamir Adleman public key encryption algorithm on standard digital signal processor, In Advances in Cryptology-Crypto’86, Springer, 1987, pp.311-323.
3.Bosselaers, R. Govaerts and J. Vandewalle, Comparison of three modular reduction functions, In Advances in Cryptology-Crypto’93, LNCS 773, Springer-Verlag, 1994, pp.175-186.
4.E. F. Brickell. A Survey of Hardware Implementations of RSA. Proceedings of Crypto’89, Lecture Notes in Computer Science, Springer-Verlag, 1990.
5.J.-F. Dhem, J.-J. Quisquater, Recent results on modular multiplications for smart cards,
Proceedings of CARDIS 1998, Volume 1820 of Lecture Notes in Computer Security, pp 350-366, Springer-Verlag, 2000
6.GNU Multiple Precision Arithmetic Library http://www.swox.com/gmp/gmp-man- 4.1.2.pdf
7.K. Hensel, Theorie der algebraische Zahlen. Leipzig, 1908
8.J. Jedwab and C. J. Mitchell. Minimum weight modified signed-digit representations and fast exponentiation. Electronics Letters, 25(17): 1171-1172, 17. August 1989.
9.D. E. Knuth. The Art of Computer Programming. Volume 2. Seminumerical Algorithms. Addison-Wesley, 1981. Algorithm 4.3.3R
10.W. Krandick, J. R. Johnson, Efficient Multiprecision Floating Point Multiplication with Exact Rounding, Tech. Rep. 93-76, RISC-Linz, Johannes Kepler University, Linz, Austria, 1993.
11.A.Menezes, P.van Oorschot, S.Vanstone, Handbook of Applied Cryptography, CRC Press, 1996.
12.P.L. Montgomery, Modular Multiplication without Trial Division, Mathematics of Computation, Vol. 44, No. 170, 1985, pp. 519-521.
13.J.-J. Quisquater, Presentation at the rump session of Eurocrypt’90.
14.R. L. Rivest; A. Shamir, and L. Adleman. 1978. A method for obtaining digital signatures and public key cryptosystems. Communications of the ACM 21(2):120--126
TEAM LinG
Long Modular Multiplication for Cryptographic Applications |
61 |
15.SNIA OSD Technical Work Group http://www.snia.org/tech_activities/workgroups/osd/
16.C. D. Walter, Faster modular multiplication by operand scaling, Advances in Cryptology, Proc. Crypto’91, LNCS 576, J. Feigenbaum, Ed., Springer-Verlag, 1992, pp. 313—323
17.L. Hars, manuscript, 2003.
TEAM LinG

Leak Resistant Arithmetic
Jean-Claude Bajard1, Laurent Imbert2, Pierre-Yvan Liardet3, and
Yannick Teglia3
1 LIRMM, CNRS, Université Montpellier II
161 rue Ada, 34392 Montpellier cedex 5, France
bajard@lirmm.fr
2 LIRMM, CNRS, France, and
ATIPS†, CISaC‡, University of Calgary
2500 University drive N.W, Calgary, T2N 1C2, Canada
Laurent.Imbert@lirmm.fr,
3 STMicroelectronics, Smartcard ICs
Z.I. Rousset, 13106 Rousset Cedex, France
{Pierre-Yvan.Liardet,Yannick.Teglia}@st.com
Abstract. In this paper we show how the usage of Residue Number Systems (RNS) can easily be turned into a natural defense against many side-channel attacks (SCA). We introduce a Leak Resistant Arithmetic (LRA), and present its capacities to defeat timing, power (SPA, DPA) and electromagnetic (EMA) attacks.
Keywords: Side channel attacks, residue number systems, RNS Montgomery multiplication.
1Introduction
Side-channel attacks rely on the interactions between the component and the real world. Those attacks formerly appeared in the network security world and eventually came within the smartcard and embedded system world to become the most pertinent kind of attacks on secure tokens. Some attacks monitor the computation through its time execution or its power consumption in order to discover secrets, as shown by P. Kocher in [19,18]. Some others try to modify the component’s behavior or data, through fault injection as pointed out first by D. Boneh, R. A. DeMillo, and R. J. Lipton in [6] in the case of public-key protocols, and extended to secret-key algorithms by E. Biham and A. Shamir in [5]. From noise adding to whole algorithm randomization, different ways have been considered to secure the implementations against side channels [19], and especially against power analysis [18,12]. One difficult task when preventing from SCA is to protect from differential power analysis (DPA) introduced by P. Kocher in [18] and its equivalent for electromagnetic attacks (EMA) [9,1], and recent
† Advanced Technology Information Processing Systems
‡ Center for Information Security and Cryptography
M. Joye and J.-J. Quisquater (Eds.): CHES 2004, LNCS 3156, pp. 62–75, 2004. |
|
© International Association for Cryptologic Research 2004 |
TEAM LinG |
Leak Resistant Arithmetic |
63 |
multi-channel attacks [2]. These specific attacks take advantage of correlations between the internal computation and the side channel information.
The purpose of Leak Resistant Arithmetic (LRA) is to provide a protection at the arithmetic level, i.e. in the way we represent the numbers for internal computations. We show how the usage of Residue Number Systems (RNS), through a careful choice of the modular multiplication algorithm, can easily be turned into a natural defense against SCA. In the same time, our solution provides fast parallel implementation and enough scalability to support key-size growth induced by the progress of classical cryptanalysis and computational power. In addition, another advantage of LRA is that classical countermeasures still apply at the upper level. We illustrate this fact in Sect. 3.3 through an adaptation to LRA of the Montgomery ladder [23], which has been analyzed in the context of side-channels [15], and which features (C safe-error and M safe-error protected) make it a first-class substitute to the square-and-multiply algorithm.
This paper puts together previous works from J.-C. Bajard and L. Imbert on RNS Montgomery multiplication and RSA implementation [3,4], and P.-Y. Liardet original idea of addressing SCA using RNS, proposed in September 2002 in [20]. The same idea has been independently investigated by M. Ciet, M. Neeve, E. Peeters, and J.-J. Quisquater, and recently published in [8]. In Sect. 3.1, we address the problem of the Montgomery factor when RNS bases are randomly chosen, and we propose solutions which make it possible to randomly select new RNS bases during the exponentiation in Sect. 3.3.
2The Residue Number Systems
In RNS, an integer X is represented according to a base of relatively prime numbers, called moduli, by the sequence
of relatively prime numbers, called moduli, by the sequence  where
where  for
for  The conversion from radix to RNS is then easily performed. The Chinese Remainder Theorem (CRT) ensures the uniqueness of this representation within the range
The conversion from radix to RNS is then easily performed. The Chinese Remainder Theorem (CRT) ensures the uniqueness of this representation within the range  where
where  The constructive proof of this theorem provides an algorithm to convert X from its residue representation to the classical radix representation:
The constructive proof of this theorem provides an algorithm to convert X from its residue representation to the classical radix representation:
where  and
and  is the inverse of
is the inverse of  modulo
modulo  In the rest of the paper,
In the rest of the paper,  denotes the remainder of X in the division by
denotes the remainder of X in the division by  i.e. the value
i.e. the value
One of the well known advantages of RNS is that additions, subtractions and multiplications are very simple and can be efficiently implemented on a parallel architecture [17]. Furthermore, only the dynamic range of the final result has to be taken into account since all the intermediate values can be greater than M.
TEAM LinG

64 J.-C. Bajard et al.
On the other hand, one of the disadvantages of this representation is that we cannot easily decide whether  is greater or less1 than
is greater or less1 than 
For cryptographic applications, modular reduction (X mod N), multiplication (XY mod N) and exponentiation  are the most important operations. Many solutions have been proposed for those operations. For example, it is well known that they can be efficiently computed without trial division using Montgomery algorithms [22].
are the most important operations. Many solutions have been proposed for those operations. For example, it is well known that they can be efficiently computed without trial division using Montgomery algorithms [22].
Let us briefly recall the principles of Montgomery multiplication algorithm.
Given two integers |
N such that |
and |
Mont- |
gomery multiplication evaluates |
by computing the value |
||
such that XY+QN is a multiple of |
Hence, the quotient |
is |
|
exact and easily performed. The result is less than 2N. More detailed discussions on Montgomery reduction and multiplication algorithms can be found in [21,7].
2.1RNS Montgomery Multiplication
In this section we recall a recent RNS version of the Montgomery multiplication algorithm, previously proposed in [3,4]. In the RNS version of the Montgomery multiplication, the value
is chosen as the Montgomery constant (instead of  in the classical representation). Hence, the RNS Montgomery multiplication of A and B yields
in the classical representation). Hence, the RNS Montgomery multiplication of A and B yields
where R, A, B and N are represented in RNS according to a predefined base  As in the classical Montgomery algorithm we look for an integer Q such that (AB + QN) is a multiple of
As in the classical Montgomery algorithm we look for an integer Q such that (AB + QN) is a multiple of  However, the multiplication by
However, the multiplication by  cannot be performed in the base
cannot be performed in the base  We define an extended base
We define an extended base  of
of  extra relatively prime moduli and perform the multiplication by
extra relatively prime moduli and perform the multiplication by  within this new base
within this new base  For simplicity we shall consider that both
For simplicity we shall consider that both  and
and  are of size
are of size  Let us define
Let us define  and
and  with
with  and
and
Now, in order to compute Q, we use the fact that (AB + QN) must be a multiple of  Clearly
Clearly  and thus
and thus
As a result, we have computed a value  such that
such that 
 As pointed out previously we compute (AB + QN) in the extra base
As pointed out previously we compute (AB + QN) in the extra base  Before we can evaluate (AB + QN) we have to know the product AB in base
Before we can evaluate (AB + QN) we have to know the product AB in base  and extend Q, which has just been computed in base
and extend Q, which has just been computed in base  using (4), in base
using (4), in base
1 According to the CRT testing the equality of two RNS numbers is trivial.
TEAM LinG

Leak Resistant Arithmetic |
65 |
 We then compute
We then compute 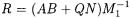 in base
in base  and extend the result back to the base
and extend the result back to the base  for future use (the next call to Montgomery multiplication). Algorithm 1 describes the computations of our RNS Montgomery multiplication. It computes the Montgomery product
for future use (the next call to Montgomery multiplication). Algorithm 1 describes the computations of our RNS Montgomery multiplication. It computes the Montgomery product  where A,B, and N are represented in RNS in both bases
where A,B, and N are represented in RNS in both bases  and
and 
Steps 1, 2 and 4 of algorithm 1 consist of full RNS operations and can be performed in parallel. As a consequence the complexity of the algorithm clearly relies on the two base extensions of lines 3 and 5.
Many different methods have been proposed to perform the base extension. Among those based on the CRT, [24] and [16] use a floating-point like dedicated unit, [26] proposes a version with an extra modulo greater than  (this method is not valid for the first extension of Algorithm 1), [25] perform an approximated extension, and [3] allow an offset for the first base extension which is compensated during the second one. Other solutions have been proposed which use the mixed radix system (MRS) [10]. The great advantage of the MRS approach is that the modification of one modulus, only requires the computation of at most
(this method is not valid for the first extension of Algorithm 1), [25] perform an approximated extension, and [3] allow an offset for the first base extension which is compensated during the second one. Other solutions have been proposed which use the mixed radix system (MRS) [10]. The great advantage of the MRS approach is that the modification of one modulus, only requires the computation of at most  new values.
new values.
In [8], Posch and Posch’s RNS Montgomery algorithm [25] is used, together with J.-C. Bajard et al. base extensions [3], which requires the computation of  and
and  for each modulus
for each modulus  where
where  is about the same size as M, i.e. about 512 bits. In the context of random bases, precomputations are inconceivable (their choices of parameters lead to more than
is about the same size as M, i.e. about 512 bits. In the context of random bases, precomputations are inconceivable (their choices of parameters lead to more than  possible values for M). So we suppose that they evaluate these values at each base selection. Note that our algorithm uses the MRS conversion to avoid this problem.
possible values for M). So we suppose that they evaluate these values at each base selection. Note that our algorithm uses the MRS conversion to avoid this problem.
2.2Modular Exponentiation
The RNS Montgomery multiplication easily adapts to modular exponentiation algorithms. Since the exponent is not represented in RNS, we can consider any
TEAM LinG
