21. Балки расчет балок с гибкой стенкой и ребрами

21.1 (18.2*).Расчетные формулы приведены для балок со стенками, подкрепленными поперечными ребрами жесткости, несущих статическую нагрузку, с относительной гибкостью стенки, находящейся в пределах от 6 до 13. Ограничение сверху сделано для предотвращения выпучивания в плоскости стенки сжатых поясов балки, выполняемых из листовой стали. Ограничение снизу указано ориентировочно, в связи с чем этим методом расчета можно пользоваться и при< 6, если проверка выполняется в соответствии с пп. 7.1, 7.2*, 7,3, 7.4* СНиПII-23-81*. Сущность применяемого метода состоит в учете закритической стадии работы стенки.

21.2 (18.2*).Наиболее полное решение для балки симметричного двутаврового сечения при чистом изгибе получено в работе [31]. Придельное значение моментаМ_инайдено из выражения, аппроксимирующего точное решение:

М_и/(WR_y) = (+ 0,224)/(+ 0,224), (145)

где =A_f/A_w;= 0,259 + 1,945/(- 1,1).

В табл. 63 приведены значения предельных моментов, вычисленные по формуле (145).

Таблица 63

Значение 	Значения Ми/(WRy) при , равной
	8	10	12	14
0,5	0,858	0,838	0,826	0,817
1,0	0,916	0,904	0,897	0,892
2,0	0,954	0,947	0,943	0,940

Эпюры предельных мембранных напряжений _х[31] показывают, что в зоне растяжения эпюра близка к линейной, но краевое напряжение не достигает предела текучести. Для практических расчетов в СНиПII-23-81* принята упрощенная схема предельного состояния, в которой сжатая зона стенки представляет собой прямоугольник высотойh₁с напряжением, равным расчетному сопротивлениюR_y(рис. 47). Краевое растягивающее напряжение также принято равным по абсолютной величинеR_y.При малой толщине поясов по сравнению с высотой стенки и получена формула (159) СНиПII-23-81*, которая дает несколько преувеличенные (от 1 до 3,6 %) значенияМ_и, поскольку в действительной эпюре напряжений в растянутом поясе расчетное сопротивление не достигается.

Рис. 47. Схема предельного состояния сечения балки при изгибе

а - сечение балки; б - эпюра напряжений

21.3 (18.2*).Поперечная силаQ_u, воспринимаемая стенкой, слагается из двух частей: силыQ_cr=_срht, отвечающей критической нагрузке, и дополнительной силыQ,возникающей в закритической стадии вследствие образования диагональной или близкой к ней растянутой полосы. Различные модели отличаются углом наклона и шириной этой полосы, а также значением предельного растягивающего напряжения (распределение напряжений обычно считается равномерным). В работе [32] принято, что ось полосы совпадает с диагональю (рис. 48), а ширина полосы определяется положением пластического шарнира, возникающего вследствие изгиба пояса. В сечение пояса включается полоса стенки шириной от 0 до 30tв зависимости от_ср/R_y. Предельное напряжение растяжения в диагональной полосе находится из условия, чти интенсивность напряжений равна пределу текучести.

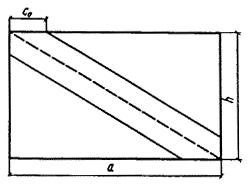
Рис. 48. Схема отсека стенки балки при сдвиге

Метод Рокки-Шкалоуда [32] можно существенно упростить посредством допущений, ведущих к некоторому уменьшению предельной нагрузки. Этот вариант реализован в СНиП II-23-81*.

Предельное касательное напряжение в стенке _uопределяется из выражения

, (146)

где  = a/h;

_cr- критическое касательное напряжение;

c_o/a- определяется из формул:

(147)

;

W_p- пластический момент сопротивления сечения пояса, в который включается полоса стенки шириной ; при вычислениях по формуле (162) СНиПII-23-81* для упругого тавра вместоW_pподставляется 2W_min.

Если в практических расчетах получается, что c_o/a> 0,4, то необходимо приниматьc_o/a= 0,4. Значение_crследует вычислять с учетом упругого защемления стенки в поясах, например, по формуле (76) СНиПII-23-81*. Из формулы (146) настоящего Пособия получена формула (160) СНиПII-23-81*.

21.4 (18.3).В описанной модели предельного состояния закритическая работа стенки обусловлена появлением диагональной растянутой полосы, следовательно, ребро должно выполнять роль сжатой стойки и воспринимать усилиеQ= (_u-_cr)ht.

В сечение ребра можно включить часть стенки по 0,65tс каждой стороны. При проверке прочности и устойчивости одностороннего ребра следует учитывать эксцентриситет сжимающей силы, равный расстоянию от срединной плоскости стенки до центра тяжести сечения ребра. Этот способ расчета приведен в СНиПII-23-81*.

21.5 (18.2).Комбинация изгиба со сдвигом теоретически рассмотрена с использованием обычных допущений (упругая пластинка, условные критерии предельного состояния). Кривая взаимодействия момента и поперечной силы близка к известной кривой для критических нагрузок. Истинная кривая должна быть более выпуклой, так как формы выпучивания от предельного момента и предельной поперечной силы, действующих порознь, различаются больше, чем соответствующие собственные функции линейных краевых задач.

Экспериментальная проверка выполнена на малом числе образцов, поэтому для практических расчетов обычно рекомендуются эмпирические кривые взаимодействия в координатах Q/Q_uиМ/М_и(символы без индексов относятся к комбинированному нагружению), в частности, формула (158) СНиПII-23-81*, дающая небольшой запас несущей способности.

21.6 (18.7*).Предельное значение сосредоточенной силы, приложенной к поясу (b_ft_f) двутавровой тонкостенной балки, находится из условия, что наибольшее напряжение в стенке под грузом равно расчетному сопротивлению:

F_u = 3,26tR_y,

где .

Тогда . (148)

При передаче давления через полку двутавра, лежащего на балке, или через прокладку значение F_uможно увеличить на 10%.