Закон редких событий (Пуассона)

Если вероятность Р события А очень мала (Р ≤ 0,1), а число испытаний велико, то вероятность того, что событие А наступит k раз в n испытаниях, будет равна

,

где а = n ∙ Р = E(X) — математическое ожидание числа k.

Когда число испытаний n велико, а Р мало, то закон биномиального распределения и закон редких событий практически совпадает. Это имеет место тогда, когда Р ≤ 0,1 и n ∙ Р > 4.

Рисунок - Дифференциальная функция геометрического распределения.

Пример. В партии из 1000 деталей имеется 1% брака. Какова вероятность того, что при взятии из партии выборки объемом 50 штук в ней будет находится 3 дефектных деталей.

Здесь Р = 0,01; n = 50; n ∙ Р = 50 ∙ 0,01 = 0,5

Распределение Пуассона имеет только один параметр — математическое ожидание E(X). Поэтому, когда в распределении дискретной случайной величины имало отличаются друг от друга по своим численным значениям, то можно уверенно считать, что данное распределение подчиняется закону редких событий.

Геометрическое распределение

Геометрическое распределение – распределение случайной величины X с целочисленными неотрицательными значениями, заданное формулой

где 0<p<1 – параметр. Вероятности p_m образуют геометрическую прогрессию (отсюда название – “геометрическое распределение”). Математическое ожидание и дисперсия геометрического распределения равны

Рисунок - Дифференциальная функция геометрического распределения.

Обычно геометрическое распределение возникает в схеме испытаний Бернулли (испытания Бернулли – независимые испытания с двумя случайными исходами, вероятности которых не изменяются от испытания к испытанию) и интерпретируется как распределение времени ожидания до первого успеха. Если число испытаний Бернулли заранее не ограничено и p – вероятность успеха, то случайная величина X – число испытаний, предшествующих наступлению первого успеха,– имеет геометрическое распределение. Если X₁, …, X_n – независимые случайные величины, имеющие одинаковое геометрическое распределение с параметром p, то сумма имеет распределение Паскаля.

Геометрическое распределение является единственным дискретным распределением, обладающим свойством «отсутствия последействия»: состояние некоторой системы в настоящий момент времени t₀ однозначно определяет распределение вероятностей будущего развития процесса при t>t₀, и информация о прошлом поведении процесса не влияет на это распределение.

 

Законы распределения непрерывных случайных величин Закон нормального распределения (Гаусса)

Закон нормального распределения находит большое применение в различных отраслях техники. Этому закону подчиняются многие непрерывные случайные величины, встречающиеся в технике, например, погрешности измерения, высота микронеровностей обработанной поверхности.

Из математической статистики известно, что если изучаемая величина является результатом действия нескольких независимых случайных факторов, то даже если последние нам не известны, эта величина имеет нормальное распределение.

Это положение дает объяснение тому факту, что при обработке деталей на настроенных станках действительные размеры деталей подчиняются закону нормального распределения, т.к. на разброс размеров оказывает влияние большое количество факторов, зависящих от станка, приспособления, инструмента и заготовки.

Дифференциальная функция распределения случайной величины, подчиняющейся закону нормального распределения, имеет следующее выражение

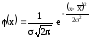
а интегральная функция распределения

Дифференциальная функция нормального распределения графически выражается кривой следующего вида.

Рисунок - Дифференциальная функция нормального распределения.

Интегральная функция нормального распределения графически выражается кривой следующего вида.

Рисунок - Интегральная функция нормального распределения.

Вероятность попадания случайной величины в интервал равна 0,9973, т.е. лишь 0,27 % значений может выйти за указанный предел. Поэтому в инженерной деятельностипринято считать достаточными пределами распределения случайной величины.

Положение кривой относительно начала координат и ее форма определяются двумя параметрами и. С изменениемформа кривой не изменяется, но изменяется ее положение относительно начала координат. С изменениемположение кривой не изменяется, но изменяется ее форма. С уменьшениемкривая становится более вытянутой, а ветви ее сближаются.

В процессе изготовления деталей машин качество их изготовления зависит от технологических факторов, в большей или меньшей степени влияющих на точность обработки. Часть из этих факторов является причиной систематических погрешностей, которые носят постоянный или переменный характер.

Другая часть факторов, влияющих на точность обработки, является причиной случайных погрешностей, приводящих к рассеянию размеров деталей в пределах поля допуска. Случайные погрешности возникают вследствие колебания величин припусков в различных деталях, различных параметров.

Если после измерения партию деталей разбить на группы с одинаковыми размерами, и отклонениями и построить графическую зависимость, то получим кривую распределения размеров, которая характеризует точность обработки деталей. Случайные погрешности в размерах обрабатываемых деталей подчиняются закону нормального распределения, который графически изображается кривой Гаусса.