
- •Основные вопросы учебной программы по физике (1 семестр)
- •5. Центр масс механической системы и закон его движения.
- •11. Удар абсолютно упругих и неупругих тел. Превращения энергии и законы сохранения.
- •12. Момент импульса и момент силы относительно неподвижной точки. Момент импульса и момент силы относительно неподвижной оси.
- •13. Закон сохранения момента импульса материальной точки и системы материальных точек.
- •14. Момент инерции относительно неподвижной оси вращения. Теорема Штейнера. Кинетическая энергия вращающегося тела. Момент инерции тонкого стержня. Работа и мощность при вращении твердого тела.
- •15. Преобразования Галилея. Механический принцип относительности. Специальная и общая теория относительности. Принцип эквивалентности.
- •16. Постулаты специальной теории относительности. Преобразования Лоренца.
- •28. Волновая поверхность. Фронт волны. Сферическая волна. Затухающие волны. Плоская волна. Фазовая скорость и дисперсия волн.
- •29. Энергия волны. Плотность энергии. Средний поток. Плотность потока. Вектор Умова.
- •30. Принцип суперпозиции волн. Интерференция волн. Когерентность. Уравнение стоячей волны и его анализ.
- •32. Опытное обоснование корпускулярно-волнового дуализма вещества. Формула де Бройля. Экспериментальное подтверждение гипотезы де Бройля.
- •33. Волновая функция и ее физический смысл. Временное и стационарное уравнения Шредингера. Стационарные состояния. Собственные функции и собственные значения.
- •34. Соотношение неопределенностей. Ограниченность механического детерминизма.
- •35. Свободная частица. Частица в одномерной потенциальной яме. Квантование энергии и импульса частицы. Принцип соответствия Бора.
- •36. Квантовый гармонический осциллятор. Влияние параметров потенциальной ямы на квантование энергии. Туннельный эффект.
- •37. Статистический метод исследования. Вывод уравнения молекулярно-кинетической теории газов для давления. Средняя кинетическая энергия молекул.
- •39. Закон Максвелла для распределения частиц идеального газа по скоростям и энергии теплового движения. Физический смысл функции распределения. Характеристические скорости.
- •46. Применение первого начала термодинамики к изопроцессам и адиабатическому процессу в идеальном газе. Зависимость теплоемкости идеального газа от вида процесса.
- •47. Обратимые и необратимые процессы. Круговой процесс. Цикл Карно и его к.П.Д. Для идеального газа. Тепловые машины.
- •48. Второе начало термодинамики. Энтропия. Энтропия идеального газа.
- •49. Статистическое толкование второго начала термодинамики.
- •50. Реальные газы. Отступления законов реальных газов от законов для идеальных газов. Силы и потенциальная энергия межмолекулярного взаимодействия. Уравнение Ван-дер-Ваальса.
- •51. Изотермы реального газа. Опыт Эндрюса. Критические параметры.
- •52. Внутренняя энергия реального газа. Эффект Джоуля-Томсона.
- •53. Фазовые переходы первого и второго рода.
- •54. Классические представления о теплоемкости твердых тел. Теория Эйнштейна. Теория Дебая.
- •55. Понятие о фононах. Статистика фононного газа. Плотность состояний.
- •57. Статистика Ферми-Дирака и Бозе-Эйнштейна. Фермионы и бозоны. Квантовые числа. Спин электрона. Принцип неразличимости тождественных частиц. Принцип Паули.
28. Волновая поверхность. Фронт волны. Сферическая волна. Затухающие волны. Плоская волна. Фазовая скорость и дисперсия волн.
Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью.
Геометрическое место точек, до которых доходят колебания к моменту времени t, называется волновым фронтом.
Сферическая волна – поверхности, которые представлены в виде совокупность концентрических сфер.
Плоская волна - поверхности, которые представлены в виде совокупности плоскостей, параллельных друг другу.
Фазовая скорость – скорость перемещения фазы волны.
Если фазовая скорость волн в среде зависит от их частоты, то это явление называют дисперсией волн.
29. Энергия волны. Плотность энергии. Средний поток. Плотность потока. Вектор Умова.
Перенос энергии волнами количественно характеризуется вектором плотности потока энергии.
30. Принцип суперпозиции волн. Интерференция волн. Когерентность. Уравнение стоячей волны и его анализ.
При распространении в линейной среде нескольких волн каждая из них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые получают частицы, участвуя в каждом из слагающих волновых процессов.
Интерференция - при наложении в пространстве двух (или нескольких) когерентных волн в разных его точках получается усиление или ослабление результирующей волны в зависимости от соотношения между фазами этих волн.
Согласованное протекание во времени и пространстве нескольких колебательных или волновых процессов называют когерентностью.
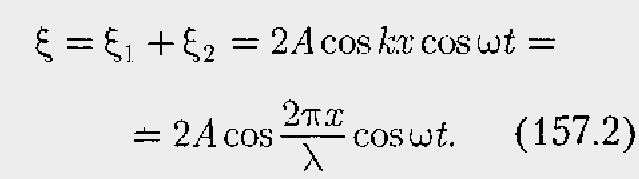
32. Опытное обоснование корпускулярно-волнового дуализма вещества. Формула де Бройля. Экспериментальное подтверждение гипотезы де Бройля.
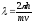 При
отражении частиц от кристаллической
решетки возникает разность хода.
При
отражении частиц от кристаллической
решетки возникает разность хода.
33. Волновая функция и ее физический смысл. Временное и стационарное уравнения Шредингера. Стационарные состояния. Собственные функции и собственные значения.
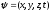 Квадрат
модуля волновой функции (квадрат модуля
амплитуды волн де Бройля) определяет
вероятность нахождения частицы в момент
времени t
в области с координатами (x,
y,
z).
Квадрат
модуля волновой функции (квадрат модуля
амплитуды волн де Бройля) определяет
вероятность нахождения частицы в момент
времени t
в области с координатами (x,
y,
z).
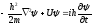 Временное
уравнение, где i-мнимая
единица.
Временное
уравнение, где i-мнимая
единица.
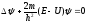 Стационарное
уравнение.
Стационарное
уравнение.
Стационарные состояния – состояния с фиксированными значениями энергии.
Значения энергии называются собственными. Решения же, которые соответствуют собственным значениям энергии, называются собственными функциями.
34. Соотношение неопределенностей. Ограниченность механического детерминизма.
![]()
Для микрочастицы не существует состояний, в которых ее координаты и импульс имели бы одновременно точные значения.
Соотношение неопределенностей является, таким образом, квантовым ограничением применимости классической механики к микрообъектам.
35. Свободная частица. Частица в одномерной потенциальной яме. Квантование энергии и импульса частицы. Принцип соответствия Бора.
Свободная частица — частица, движущаяся в отсутствие внешних полей.
Принцип соответствия Бора (1923), согласно которому законы квантовой механики должны при больших значениях квантовых чисел переходить в законы классической физики.
Уравнение Шредингера для стационарных состояний в случае одномерной задачи запишется в виде:
![]()
По условию задачи (бесконечно высокие стенки), частица не проникает за пределы ямы, поэтому вероятность ее обнаружения (а следовательно, и волновая функция) за пределами ямы равна нулю.
Квантованные значения энергии Е называются уровнями энергии, а число n, определяющее энергетические уровни частицы, называется главным квантовым числом. Таким образом, микрочастица в потенциальной яме с бесконечно высокими стенками может находиться только на определенном энергетическом уровне Е, или, как говорят, частица находится в квантовом состоянии n.
![]()
![]()
