Затухающие колебания

В случае, когда на маятник во время движения действует сила сопротивления, колебания становятся затухающими, т.е. их амплитуда постепенно убывает. Для описания таких колебаний в уравнение (10), наряду с моментами сил упругости, следует добавить момент сил сопротивления (трения), который можно представить как:

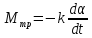, (11)

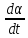
где производная представляет собой угловую скорость вращения маятника, k- постоянный коэффициент, знак «-» указывает на то, что момент сил сопротивления противоположен по направлению движения маятника. В результате уравнение движения системы примет более сложный вид:

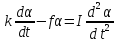. (12)

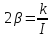
Введя обозначения , , 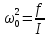преобразуем к виду:

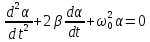. (13)

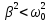
При условии, что силы сопротивления относительно невелики (выполняется условие ) решение этого уравнения примет вид:

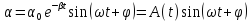
, (14)

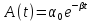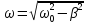
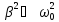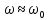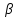
где - амплитуда колебаний, зависящая от времени; - циклическая частота затухающих колебаний, причем, когда , то ,. Коэффициент получил название коэффициента затухания. Коэффициент затухания обратен по величине тому промежутку времени, за который амплитуда уменьшается в е раз:

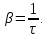
График такого колебательного процесса представлен на рисунке 2:

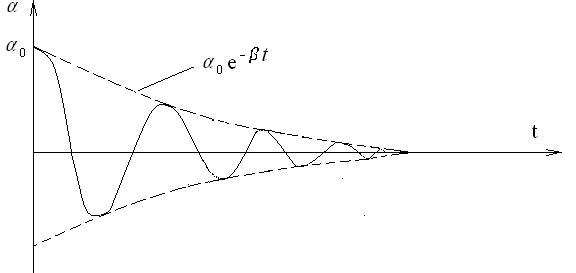
Рис.2. График затухающих колебаний

На практике вместо коэффициента затухания 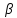используют другие, связанные с 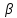величиной:

а) декремент затухания ψ (отношение амплитуд колебаний для двух соседних периодов):

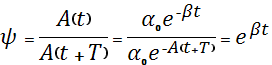
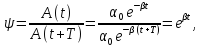(15)

б) логарифмический декремент затухания λ:

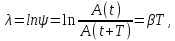
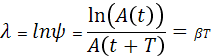(16)

в) добротность колебательной системы Q:

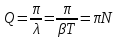
, (17)

где N-число колебаний, после которых амплитуда уменьшается в е  2.72 раза.

При слабом затухании колебаний добротность с точностью до множителя 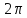равна отношению энергии, запасенной в системе в данный момент, к убыли энергии за один период колебаний. Таким образом, из приведенной теории колебаний крутильного маятника видно, что период колебаний такого маятника непосредственно связан с моментом инерции маятника модулем упругости струны, а в случае затухающих колебаний и с коэффициентом затухания и с производными от него величинами. Полученные соотношения можно использовать для определения некоторых из входящих в эти соотношения величин экспериментальным путем.

Методика выполнения работы

Лабораторная установка

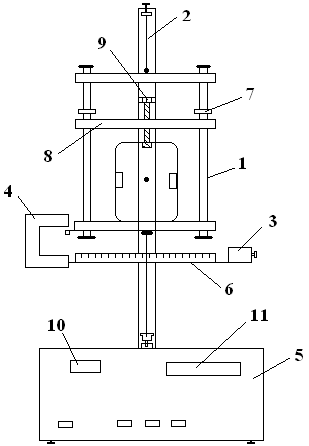
Рис. 3. Лабораторная установка

Лабораторная установка состоит из колебательной системы (держатель 1 и струна 2), магнита 3, фотоэлектрического датчика 4, электронного устройства 5 для измерения периода и числа колебаний и шкалы 6 для измерения угловой амплитуды. Цанговые устройства 7 служат для крепления перемычки 8, а винт 9 — для крепления тел в держателе. Для измерения периода колебаний маятника необходимо нажать кнопку «сброс» и повернуть маятник на такой угол, при котором электромагнит будет его удерживать. Нажать кнопку «пуск». В окошках 10 и 11 электронного устройства появляются текущие отчеты числа периодов и времени соответственно. Нажать кнопку «стоп». Рассчитать период колебаний, разделив время на число колебаний.

Вывод рабочей формулы

Определение модуля кручения струны и неизвестного момента инерции тела

Отклоним крутильный маятник на угол α. Запасенная потенциальная энергия будет при этом равна

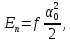(18)

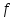
где - модуль кручения струны, α - угол отклонения.

При прохождении положения равновесия маятник имеет max. кинетическую энергию, равную

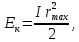(19)

где ––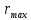 максимальная угловая скорость маятника.

Угловая скорость

,

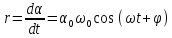следовательно

.

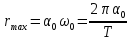
Поэтому

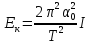, (20)

где T - период колебаний, I - момент инерции маятника.

Хотя колебания затухающие, можно полагать, что в пределах одного периода убыль энергии невелика и максимальная потенциальная энергия равна максимальной кинетической. На этом основании приравняем (18) и (20):

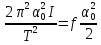. (21)

Установим в держатель маятника куб таким образом, чтобы ось вращения проходила перпендикулярно граням куба через его центр масс. В этом случае можно записать:

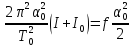, (22)

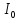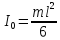
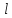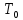
где ––момент инерции куба, который рассчитывается по формуле (где m-масса куба, - длина ребра куба). - период колебаний маятника с закрепленным в нем кубом.

Если начальные углы отклонения маятника в обоих опытах равны, то правые части (20) и (21) также равны и мы можем приравнять их левые часть:

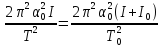. (23)

Выразим отсюда момент инерции маятника :

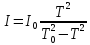
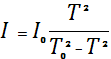. (24)

Пусть в держателе закреплено тело с неизвестным моментом инерции 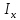. На основании закона механической энергии можно записать равенство, аналогично равенству (23):

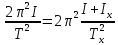. (25)

Откуда получим формулу для расчета

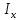
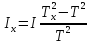, (26)

где 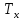- период колебаний маятника с исследуемым телом.

Период крутильных колебаний в общем виде выражается формулой (10). Запишем эту формулу для маятника с укрепленным в держателе кубом:

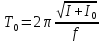. (27)

И получим выражение для расчета модуля кручения струны :

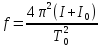. (28)

Изучение затухающих колебаний;

Пусть в некоторый момент 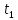амплитуда затухающих колебаний равна

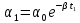. (29)

А в некоторый момент времени 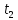спустя некоторый интервал времени Т равна :

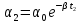. (30)

Разделим (29) на (30)

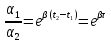. (31)

Прологарифмируем формулу (31) и выразим коэффициент затухания:

.

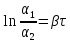Откуда

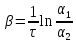. (32)

Теперь можно определить логарифмический декремент затухания и добротность колебательной системы :

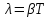. (33)

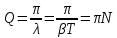. (34)