- •Пояснительная записка к курсовому проекту по теме: «Разработка кинематики, кинематической настройки главного привода токарно-затыловочного станка»
- •Аннотация
- •Содержание
- •Введение
- •1 Описание компоновки, основных узлов и движений токарно-затыловочного станка прототипа модели 1811
- •2 Технологические схемы обработки и движения формообразования
- •3 Принцип образования поверхностей и методы получения их производящих линий
- •4 Структурная схема токарно-затыловочного станка 1811 и расчетное перемещение кинематических цепей
- •5.2 Кинематическая цепь затыловочно-делительного движения (п2)
- •5.3 Кинематическая цепь продольной подачи суппорта (п3)
- •5.4 Кинематическая цепь дифференциального движения (п4)
- •5.5 Кинематическая цепь движение образования винтовой линии (п5)
- •6. Расчет мощности главного привода
- •7.7 Построение структурной сетки множительной структуры
- •7.8 Определение числа делений изображающих частоту вращения электродвигателя
- •7.9 Разбивка числа делений, изображающих частоту вращения электродвигателя, на отдельные групповые передачи
- •7.10 Построение графика частот главного привода со ступенчатым приводом
- •7.11 Определение передаточных отношений и передаточных чисел
- •7.12 Подбор чисел зубьев зубчатых колес
- •7.13 Разработка кинематической схемы главного привода со ступенчатым регулированием
- •8 Расчет крутящих моментов на валах
- •8.7 Расчет крутящего момента на шпинделе
- •9.1.4 Проектный расчет постоянной прямозубой зубчатой передачи на выносливость зубьев при изгибе
- •9.1.5 Определение модуля прямозубой постоянной передачи
- •9.1.6 Расчёт геометрических параметров постоянной прямозубой передачи
- •9.2 Проектный расчет цилиндрических прямозубых передачz3–z4иz5–z6,z7–z8иz9–z10групповой передачи
- •9.2.1 Исходные данные
- •9.2.2 Выбор материала и термической обработки зубчатых колес
- •9.2.3 Проектный расчет прямозубой зубчатой передачи групповой передачи на контактную выносливость
- •9.2.4 Проектный расчет прямозубой зубчатой передачи групповой передачи на выносливость зубьев при изгибе
- •9.2.5 Определение модуля прямозубых передач групповой передачи
- •9.2.6 Расчёт геометрических параметров прямозубых передач и,игрупповой передачи
- •9.3 Проектный расчет цилиндрических прямозубых передачz11–z12иz13–z14групповой передачи
- •9.3.1 Исходные данные
- •9.3.2 Выбор материала и термической обработки зубчатых колес
- •9.3.3 Проектный расчет прямозубой зубчатой передачи групповой передачи на контактную выносливость зубьев
- •9.3.4 Проектный расчет прямозубой зубчатой передачи групповой передачи на выносливость зубьев при изгибе
- •9.3.5 Определение модуля прямозубых передач групповой передачи
- •9.3.6 Расчёт геометрических параметров прямозубых передач игрупповой передачи
- •9.4 Проектный расчет цилиндрической постоянной прямозубой передачиz15–z16
- •9.4.1 Исходные данные
- •9.4.2 Выбор материала и термической обработки зубчатых колес
- •9.4.3 Проектный расчет постоянной прямозубой зубчатой передачи на контактную выносливость
- •9.4.4 Проектный расчет постоянной прямозубой зубчатой передачи на выносливость зубьев при изгибе
- •9.4.5 Определение модуля прямозубой постоянной передачи
- •9.4.6 Расчёт геометрических параметров постоянной прямозубой передачи
- •10 Проектный расчет валов и шпинделя
- •10.1 Проектный расчет диаметров первого вала
- •10.2 Проектный расчет диаметров второго вала
5.2 Кинематическая цепь затыловочно-делительного движения (п2)
Согласует вращение шпинделя станка с вращение кулачка затылования, обеспечивает радиальное перемещения суппорта в процессе затылования. За один оборот заготовки кулачок должен выполнить число оборотов, равное числу зубьев затылуемого изделия.
Осуществляется
при малых числах оборотов шпинделя,
т.е. с применением перебора либо
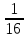 или
или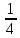 по следующей кинематической цепи:
шпиндель, зубчатая пара
по следующей кинематической цепи:
шпиндель, зубчатая пара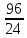 ,
валVӀ,
зубчатые передачи
,
валVӀ,
зубчатые передачи
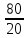 или
или
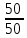 ,
валV,
зубчатая передача
,
валV,
зубчатая передача
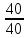 ,
вал XӀ,
гитара сменных колес
,
вал XӀ,
гитара сменных колес
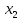 ,
дифференциал (
,
дифференциал (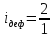 ),
зубчатая пара
),
зубчатая пара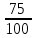 ,
валXӀӀӀ,
муфта отскока, вал XV,
коническая передача
,
валXӀӀӀ,
муфта отскока, вал XV,
коническая передача
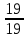 ,
кулачок.
,
кулачок.
Уравнение кинематического баланса цепи может быть записана так:
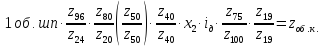
где
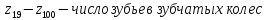
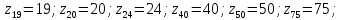
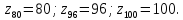
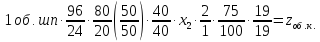
при
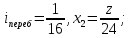
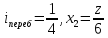 ;
;
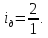
5.3 Кинематическая цепь продольной подачи суппорта (п3)
Применяется
при затыловании зубьев цилиндрических,
червячных, дисковых фрез и осуществляется
по следующей кинематической цепи:
шпиндель, цепная передача
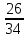 ,
вал
XVӀ,
зубчатая передача
,
вал
XVӀ,
зубчатая передача
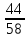 ,
вал XӀV,
тройной блок
,
вал XӀV,
тройной блок
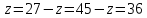 ,осуществляющий
передаточные отношения
,осуществляющий
передаточные отношения
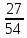 ,
,
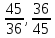 ,
валXIX,
передача
,
валXIX,
передача
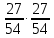 или напрямую, ходовой вал, зубчатые
передачи фартука
или напрямую, ходовой вал, зубчатые
передачи фартука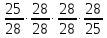 ,
червячная пара
,
червячная пара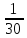 ,
кулачковая муфта, зубчатая пара
,
кулачковая муфта, зубчатая пара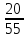 ,
подвижное реечное колесо с количеством
зубьев
,
подвижное реечное колесо с количеством
зубьев
z = 12, рейка неподвижная модуль m = 3 мм.
Уравнение баланса цепи продольной подачи суппорта запишется так:
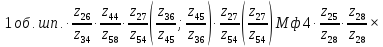
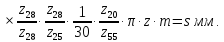
где
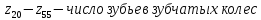
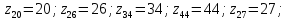
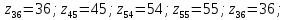
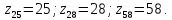
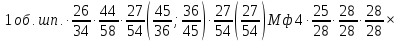
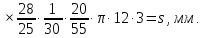
Величина подач 0,1 – 1 мм/б.
5.4 Кинематическая цепь дифференциального движения (п4)
Применяется при затыловании зубьев резьбовых изделий: метчиков, червячных фрез и осуществляется по следующей кинематической цепи:
1.
Без применения перебора. Шпиндель,
зубчатая пара
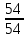 ,
валVIII,
трензель
,
валVIII,
трензель
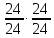 ,
валIX,
гитара сменных колес
,
валIX,
гитара сменных колес
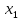 ,
валXVI,
ходовой винт с шагом t
= 12 мм.
,
валXVI,
ходовой винт с шагом t
= 12 мм.
Уравнение баланса цепи дифференциального движения запишется так:
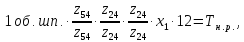
где
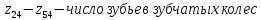
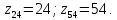
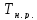 –шаг
наружной резьбы.
–шаг
наружной резьбы.
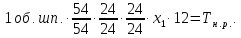
Отсюда
сменные колеса гитары:
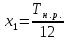 .
.
2.
С применением перебора (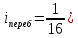 .
Шпиндель, зубчатая пара
.
Шпиндель, зубчатая пара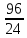 ,
валVI,
зубчатая пара
,
валVI,
зубчатая пара
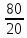 ,
валV,
зубчатая
пара
,
валV,
зубчатая
пара
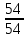 ,
валVIII,
трензель
,
валVIII,
трензель
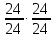 ,
валIX,
гитара сменных колес
,
валIX,
гитара сменных колес
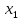 ,
валXVI,
ходовой винт с шагом t
= 12 мм.
,
валXVI,
ходовой винт с шагом t
= 12 мм.
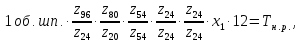
где
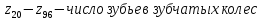
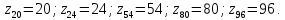
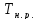 –шаг
наружной резьбы.
–шаг
наружной резьбы.
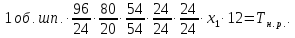
Сменные
колеса гитары:
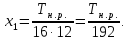
3.
С перебором (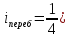 .
Шпиндель, зубчатая пара
.
Шпиндель, зубчатая пара
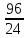 ,
валVI,
зубчатая пара
,
валVI,
зубчатая пара
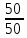 ,
валV,
зубчатая
пара
,
валV,
зубчатая
пара
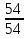 ,
валVIII,
трензель
,
валVIII,
трензель
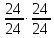 ,
валIX,
гитара сменных колес
,
валIX,
гитара сменных колес
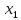 ,
валXVI,
ходовой винт с шагом t
= 12 мм.
,
валXVI,
ходовой винт с шагом t
= 12 мм.

где
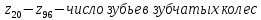
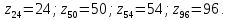
 –шаг
наружной резьбы.
–шаг
наружной резьбы.
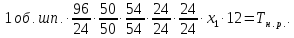
Сменные
колеса гитары:
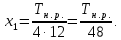
5.5 Кинематическая цепь движение образования винтовой линии (п5)
Применяется
при затыловании резьбовых изделий с
винтовыми канавками и осуществляется
по следующей кинематической цепи:
шпиндель, зубчатая пара
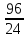 ,
валVI,
зубчатая передача
,
валVI,
зубчатая передача
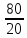 ,
или
,
или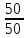 ,
валV,
зубчатая пара
,
валV,
зубчатая пара
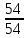 ,
валVIII,
трензель
,
валVIII,
трензель
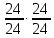 ,
валIX,
гитара сменных колес
,
валIX,
гитара сменных колес
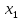 ,
валXVI,
коническая пара
,
валXVI,
коническая пара
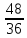 ,
валXVII,
цилиндрическая пара
,
валXVII,
цилиндрическая пара
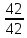 ,
валXVIII,
гитара сменных колес
,
валXVIII,
гитара сменных колес
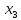 ,
червячная пара
,
червячная пара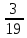 ,
дифференциал (i
= 1), зубчатая пара
,
дифференциал (i
= 1), зубчатая пара
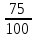 ,
валXIII,
муфта отскока, вал XV,
коническая пара
,
валXIII,
муфта отскока, вал XV,
коническая пара
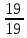 ,
кулачок.
,
кулачок.
Уравнение баланса цепи движения образования винтовой линии запишется так:
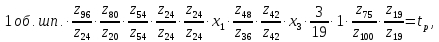
где
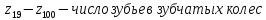
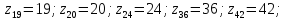
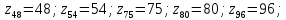
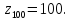
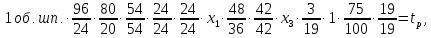
при
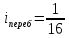 ,
,
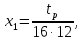
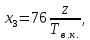
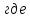
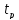 –шаг
резьбы.
–шаг
резьбы.
6. Расчет мощности главного привода
Мощность главного привода определяется по формуле:
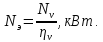
где
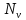 – эффективная мощность резания кВт:
– эффективная мощность резания кВт: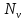 = 2,5 кВт;
= 2,5 кВт;
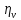 –КПД
главного привода:
–КПД
главного привода:
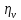 = 0,70 – 0,85.
= 0,70 – 0,85.
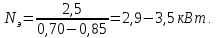
Выбираем
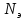 = 4 кВт, с частотой вращения электродвигателя
= 4 кВт, с частотой вращения электродвигателя
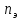 =
2850 об/мин.
=
2850 об/мин.
7 Кинематический расчет главного привода
7.1 Расчет диапазона регулирования частот вращения шпинделя
Диапазон регулирования является отношением максимальной частоты вращения шпинделя к минимальной и показывает величину возможного регулирования частоты вращения:
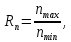
где
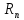 – диапазон регулирования частот вращения
шпинделя;
– диапазон регулирования частот вращения
шпинделя;
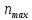 –максимальная
частота вращения шпинделя, мин-1:
–максимальная
частота вращения шпинделя, мин-1:
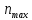 =
250 мин-1;
=
250 мин-1;
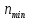 –минимальная
частота вращения шпинделя, мин-1:
–минимальная
частота вращения шпинделя, мин-1:
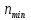 =
10 мин-1.
=
10 мин-1.
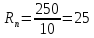
7.2 Расчет знаменателя геометрического ряда частот вращения
Рассчитывается знаменатель геометрического ряда частот вращения и приводится к стандартному значению:
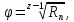
где
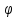 – знаменатель геометрического ряда
частот вращения шпинделя;
– знаменатель геометрического ряда
частот вращения шпинделя;
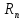 –диапазон
регулирования частот вращения шпинделя:
–диапазон
регулирования частот вращения шпинделя:
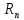 = 25;
= 25;
z – число ступеней коробки скоростей: z = 8.
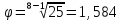
7.3 Округление знаменателя геометрического ряда частот до стандартного значения
Значения знаменателя геометрического ряда приводится к стандартному:
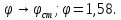
7.4 Расчет промежуточных значений частот вращения шпинделя
Промежуточные значения частот вращения шпинделя:
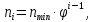
где
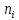 - промежуточные значения частот вращения
шпинделя;
- промежуточные значения частот вращения
шпинделя;
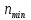 –минимальная
частота вращения шпинделя, мин-1:
–минимальная
частота вращения шпинделя, мин-1:
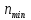 =
10 мин-1;
=
10 мин-1;
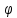 –знаменатель
геометрического ряда частот:
–знаменатель
геометрического ряда частот:
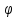 = 1,58;
= 1,58;
i – номер промежуточного значения частот вращения шпинделя.
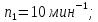
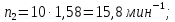
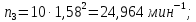
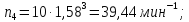
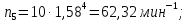
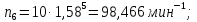
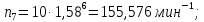
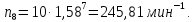
7.5 Округление частот вращения шпинделя до стандартных значений
Промежуточные
значение частот вращения шпинделя
округляются до стандартных значений:
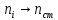 .
.
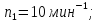
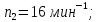
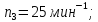
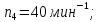
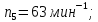
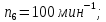
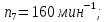
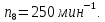
7.6 Оптимизация структурной формулы множительной структуры
Структурная формула дает информацию о конструктивном и кинематическом варианте структуры. Конструктивный вариант определяет порядок расположения групповой передачи с различным числом ступеней вдоль кинематической цепи. Кинематический вариант определяет порядок переключения групповых передач, расположенных вдоль кинематической цепи.
Структурные формулы могут иметь различные варианты:
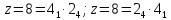 и
др.
и
др.
Оптимальным вариантом структурной формулы является тот, в котором число ступеней групповых передачи постепенно уменьшается, а характеристики постепенно возрастают, так как в этом случае будет постепенное увеличение крутящих моментов на валах, а соответственно увеличение модулей зубчатых колес и их размеров – только в последних передачах, т. е.