
13.Advanced synthesis,including PID synthesis
.pdf
22/10/2004 13.2 Synthesis using pole placement 513
to be strictly proper, then we must allow the closed-loop characteristic polynomial to have degree 2n + k. While we do not produce the explicit formula for the coe cients in NC and
˜ |
|
DC, one can easily produce such a formula by balancing polynomial coe cients, just as is |
|
done in Theorem 13.2 and Proposition 13.10. |
|
One may also wish to specify that the numerator of RC have roots at some specified locations. The following result tells us when this can be done, and the degree of the closedloop polynomial necessary to guarantee the required behaviour. We omit the details of the proof, as these go much like the proofs of Theorem 13.2 and Proposition 13.10, except that there are more complications.
13.15 Proposition Consider the interconnection of Figure 13.8 and suppose that (NP , DP ) if the c.f.r. for RP . For F R[s] a monic polynomial of degree k, the following statements hold:
(i) if deg(NP ) ≤ n − 1 and if P R[s] is monic and degree 2n + k − 1, then there exists a controller RC R(s) with c.f.r. (NC, DC) with the following properties:
(a)RC is proper;
(b)NC has F as a factor;
(c)deg(DC) = n + k − 1;
(d) the closed-loop characteristic polynomial of the interconnection, DCDP + NP NC, is exactly P ;
(ii)if deg(NP ) ≤ n and if P R[s] is monic and degree 2n + k, then there exists a controller RC R(s) with c.f.r. (NC, DC) with the following properties:
(a)RC is strictly proper;
(b)NC has F as a factor;
(c)deg(DC) = n + k;
(d) the closed-loop characteristic polynomial of the interconnection, DCDP + NP NC, is exactly P .
Note that if the GCD of NC and DP is F , then F is guaranteed to appear as a factor in the closed-loop characteristic polynomial.
13.2.3 Achievable poles using PID control We begin by noting that in this section, as in the rest of this chapter, we use a PID controller that renders proper the derivative term in the controller. Thus we take a controller transfer function of the form
RC(s) = K 1 + |
T s |
|
1 |
. |
|
|
D |
+ |
|
|
(13.5) |
||
τDs + 1 |
TI s |
|||||
The advantage of this from our point of view in this section is contained in the following result.
13.16 Lemma Let R R[s] be any rational function of the form
R(s) = a2s2 + a1s + a0 . s2 + b1s
|
514 |
|
|
|
|
13 |
Advanced synthesis, including PID synthesis |
22/10/2004 |
|||||||||||||||||||||||||||||||||||||||||
|
If one defines |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
K = |
a1b1 − a0 |
, TD = |
a0 − a1b1 + a2b12 |
, TI |
= |
a1b1 − a0 |
, τD = |
1 |
, |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
b12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b1(a1b1 − a0) |
|
|
|
|
|
|
|
|
a0b1 |
|
|
|
|
|
|
|
b1 |
|||||||||||
|
then R = RC, where RC is as in (13.5). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
Proof |
We compute |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K(1 + TD )s2 + K( |
|
1 |
|
+ |
1 |
)s + |
|
K |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τDTI |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
RC(s) = |
|
|
|
|
|
τD |
|
|
|
τD |
TI |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s2 + |
|
|
1 |
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τD |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
The lemma follows by setting |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
a2 = K(1 + |
TD |
), a1 |
= K( |
1 |
+ |
1 |
), a0 = |
K |
, b1 = |
1 |
, |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
τD |
|
|
τD |
TI |
|
|
|
|
|
|
|
|
τDTI |
|
|
|
|
τD |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
and solving for a0, a1, a2, and b1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
It is appropriate to employ a PID controller for first and second-order plants. To design |
||||||||||||||||||||||||||||||||||||||||||||||||
|
PID controllers using the machinery of Sections 13.2.1 and 13.2.2, we use Proposition 13.10 |
||||||||||||||||||||||||||||||||||||||||||||||||
|
with k = 1 to take the integrator into account. Let us see explicitly how to do this for |
||||||||||||||||||||||||||||||||||||||||||||||||
na¨ıve PID |
general first and second-order plants. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
controllers |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
with positive |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
parameters |
13.17 Proposition |
Consider the three strictly proper plant transfer functions |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω02(τs + 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τs + 1 |
|||||||||||
|
|
Rτ |
(s) = |
|
|
, |
|
Rζ,ω0 |
,τ (s) = |
|
|
|
|
|
|
|
|
|
, Rτ1,τ2,τ (s) = |
|
|
|
|
|
, |
||||||||||||||||||||||||
|
|
|
|
|
s2 + 2ζω0s + ω02 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
τs + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(τ1s + 1)(τ2s + 1) |
||||||||||||||||||||||
|
and the two polynomials |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
P1(s) = s3 + as2 + bs + c, P2(s) = s4 + as3 + bs2 + cs + d. |
|||||||||||||||||||||||||||||||||||||||||||||
|
The following statements hold: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
(i) |
if |
RP = Rτ |
and if |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
RC(s) = |
(aτ − 1)s2 + bτs + cτ − αs(τs + 1) |
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s2 + αs |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
(ii) |
for α R, then the closed-loop polynomial of the interconnection of Figure 13.8 is P1; |
|||||||||||||||||||||||||||||||||||||||||||||||
|
if |
RP = Rζ,ω0,τ and if |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a2s2 + a1s + a0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
RC(s) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s2 + b1s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
a2 |
= |
b − cτ + dτ2 − ω02 + aτω02 − 2aω0ζ − 2τω03ζ + 4ω02ζ2 |
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω02(1 + τ2ω02 − 2τω0ζ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
a |
|
= |
|
c |
|
|
|
|
dτ |
|
a − bτ + cτ2 − dτ3 + τω02 − 2ω0ζ |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
ω02 |
|
− |
ω02 |
− |
|
|
|
1 + τ2ω02 − 2τω0ζ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
a0 = |
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
ω02 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
b1 |
= |
a − bτ + cτ2 − dτ3 + τω02 − 2ω0ζ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 + τ2ω02 − 2τω0ζ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
then the closed-loop polynomial of the interconnection of Figure 13.8 is P2;
22/10/2004 |
|
|
13.2 Synthesis using pole placement |
515 |
|
(iii) if RP |
= Rτ1,τ2,τ and if |
|
|
|
|
RC(s) = |
(a2/b2)s2 + (a1/b2)s + (a0/b2) |
|
|||
s2 + (b1 |
/b2)s |
|
|
||
|
|
|
|||
a2 = −τ22 − dτ2τ12τ22 + τ1τ2(−1 + aτ2) + τ12(−1 + aτ2 − bτ22) + τ(τ1 + τ2 − aτ1τ2 + cτ12τ22) a1 = −τ1 − τ2 + aτ1τ2 − cτ12τ22 − dτ2τ1τ2(τ1 + τ2) + τ(1 − bτ1τ2 + dτ12τ22 + cτ1τ2(τ1 + τ2))
a0 = −(d(τ − τ1)τ1(τ − τ2)τ2) b2 = −(τ − τ1)(τ − τ2)
b1 = τ1 + τ2 − aτ1τ2 − cτ2τ1τ2 + dτ3τ1τ2 + τ(−1 + bτ1τ2),
then the closed-loop polynomial of the interconnection of Figure 13.8 is P2.
13.18 Remarks 1. Using Lemma 13.16 one can turn the controllers of Proposition 13.17 into
|
PID controllers of the form (13.5). |
|
2. |
Note that the three plants Rτ , Rζ,ω0,τ and Rτ1,τ2,τ cover all possible strictly proper first |
|
|
and second-order plants. |
|
3. |
The essential point is not so much the formulae themselves as their existence. That is to |
|
|
say, the main point is that for a first-order plant, a PID controller can be explicitly found |
|
|
that produces a desired third-order characteristic polynomial, and that for a second- |
|
|
order plant, a PID controller can be explicitly found that produces a desired fourth-order |
|
|
characteristic polynomial. |
|
4. |
In practice, one would not use the formulae of Proposition 13.17, but would simply |
|
|
design a controller of the type RC(s) = a2s2+a1s+a0 |
by enforcing a pole at s = 0 as in |
|
s(s+b1) |
|
|
Proposition 13.10. |
|
5. |
Note that for first-order plants, there is some freedom in the design of an appropriate PID |
|
|
controller (characterised by the presence of the parameter α in part (i) of the proposition). |
|
|
However, the PID controller of part (ii) is uniquely specified by the desired characteristic |
|
|
polynomial. |
|
Let us illustrate a PID design using Proposition 13.17.
13.19 Example (Example 12.14 cont’d) So that we may contrast our design with that of the ad hoc PID design of Section 12.2.3, we take RP = s12 . Let us design a controller with poles at {−5, −5, −2 ± 2i}. Thus we require the characteristic polynomial
P = s4 + 14s3 + 73s2 + 180s + 200.
By contrast, the closed-loop characteristic polynomial of Example 12.14 is
s3 + 134 s2 + 3910 s + 1320 ,
which has roots of approximately {−0.197, −1.53 ± 0.984i}. The lower degree of the characteristic polynomial is Example 12.14 is a consequence of the derivative term not being proper as in (13.5). In any event, an application of Proposition 13.17, or more conveniently
of Proposition 13.10, gives
RC(s) = 73s2 + 180s + 200. s(s + 14)
516 |
13 Advanced synthesis, including PID synthesis |
22/10/2004 |
|||||||||
Converting this to the PID form of (13.5) using Lemma 13.16 gives |
|||||||||||
|
580 |
|
2997 |
29 |
1 |
|
|||||
|
K = |
|
, |
TD = − |
|
, |
TI = |
|
, τD = |
|
. |
|
49 |
8120 |
35 |
14 |
|||||||
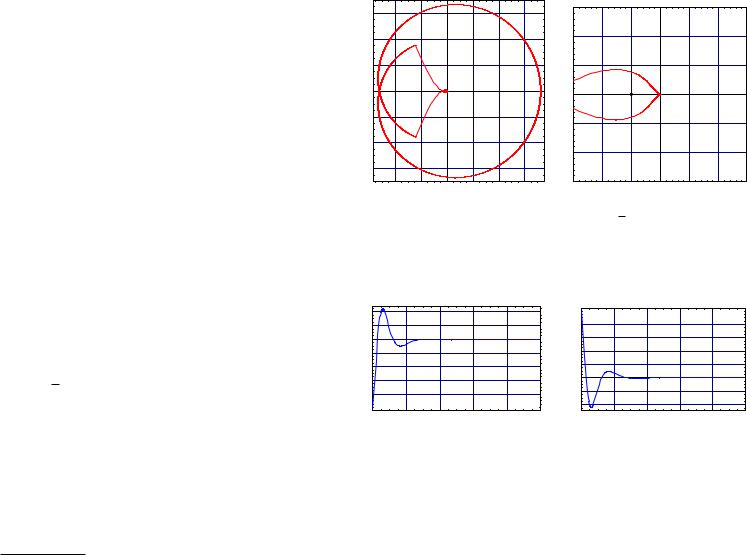
In Figure 13.12 we show the Nyquist plot for the loop gain RCRP . Note that this controller
|
60 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
Im |
0 |
|
|
|
|
Im |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-20 |
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-2 |
|
|
|
|
|
|
|
|
-60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-40 |
-20 |
0 |
20 |
40 |
60 |
|
-2 |
|
-1 |
0 |
1 |
2 |
3 |
|
|
|
Re |
|
|
|
|
|
|
|
Re |
|
|
|
|
|
Figure 13.12 |
Nyquist plot for plant RP (s) |
= |
12 |
and controller |
|
|
||||||
|
|
RC(s) = 73s2+180s+200 |
|
|
|
s |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
s(s+14) |
|
|
|
|
|
|
|
|
|
|
has o the bat presented us with respectable gain and phase margins. If one wished, this controller could be used as a starting point for further refinements to the stability margins. In Figure 13.13 is shown the step response and the response to a step disturbance between
|
1.4 |
|
|
|
|
1 |
|
1.2 |
|
|
|
|
0.8 |
|
1 |
|
|
|
|
0.6 |
(t) |
0.8 |
|
|
|
(t) |
0.4 |
|
|
|
|
|||
|
|
|
|
|
||
Σ |
|
|
|
|
Σ |
0.2 |
1 |
0.6 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
0.4 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0.2 |
|
|
|
|
-0.2 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
-0.4 |
|
|
|
|
|
|
|
|
2 |
4 |
6 |
8 |
10 |
|
|
|
|
t |
|
|
|
2 |
4 |
6 |
8 |
10 |
|
|
t |
|
|
Figure 13.13 Step response (top) and response to step disturbance (bottom)
which enters the system at the output. The response time is quite good, although the overshoot is a bit large, and could be improved with a larger derivative time, perhaps.
13.3 Two controller configurations
In the preceding section we considered the achieving of a specified closed-loop characteristic polynomial using a unity gain feedback configuration as in Figure 13.8. Next we
22/10/2004 |
13.3 Two controller configurations |
517 |
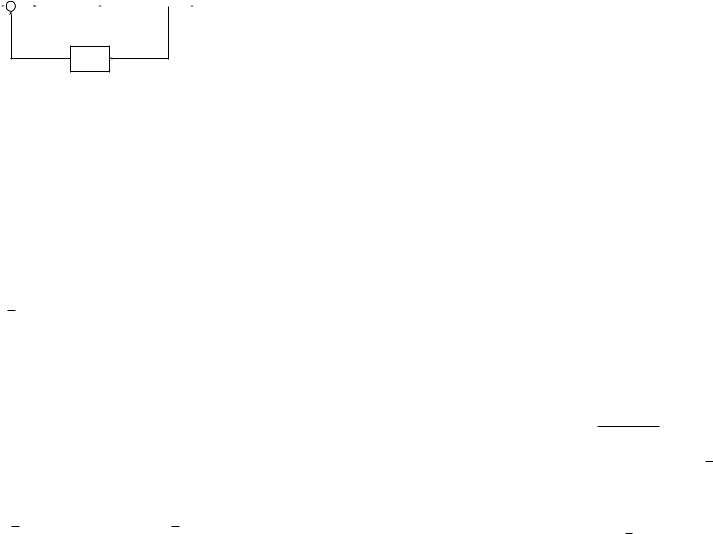
turn our attention to a richer specification of the closed-loop transfer function to allow the determination of not only the closed-loop characteristic polynomial, but also additional features of the closed-loop transfer function. To do this we must consider a more complicated interconnection, and we consider the interconnection of Figure 13.14. There are now two
rˆ(s) |
|
|
|
|
R (s) |
|
|
RP (s) |
|
yˆ(s) |
− |
|
|
||||||||
|
|
|
|
|
|
|
||||
Rfb(s)
Figure 13.14 A two controller feedback loop
controllers we may specify, and we call Rfb the feedback controller and R the feedforward controller. It certainly makes sense that having two controllers makes it possible to do more than was possible in Section 13.2. The objective of this section is to quantify how much can be done with the richer configuration, and to detail exactly how to do what is possible.
13.3.1 Implementable transfer functions First let us be clear about what we are after.
13.20 Definition Let RP R(s) be a proper plant. R R(s) is implementable for RP if there exists proper feedback and feedforward controllers Rfb, R R(s) so that
(i)R is the closed-loop transfer function for the interconnection of Figure 13.14,
(ii)the interconnection is IBIBO stable, and
(iii)the only zeros of R in C+ are those of RP , including multiplicities.
We denote by I (RP ) the collection of implementable closed-loop transfer functions for the plant RP .
The next result tells us that it is possible to achieve an implementable transfer function with an interconnection of the form Figure 13.14.
13.21 Theorem Let RP be a proper plant with c.f.r. (NP , DP ), and let R R(s) have c.f.r. (N, D). The following conditions are equivalent.
(i) |
R is implementable; |
|
||
|
|
R |
+ |
|
(ii) |
R, |
|
RH∞ and the strictly nonminimum phase zeros of R and RP |
agree, including |
RP |
||||
multiplicities;
(iii)the following three conditions hold:
(a)D is Hurwitz;
(b)deg(D) − deg(N) ≥ deg(DP ) − deg(NP );
(c)the roots of N in C+ are exactly the roots of N in C+, including multiplicities.
518 |
13 Advanced synthesis, including PID synthesis |
22/10/2004 |
Proof (i) = (ii) If R is implementable, the interconnection of Figure 13.14 is IBIBO stable. In particular, the closed-loop transfer function is IBIBO stable, and since this is by hypothesis R, we have R RH+∞. The transfer function from the plant input uˆ to the reference rˆ should also be BIBO stable. This means that
|
|
|
uˆ |
|
y/ˆ rˆ |
|
R |
|
|
|
|
||||||
|
|
|
|
|
= |
|
|
= |
|
|
RH∞+ . |
|
|
|
|
||
|
|
|
rˆ |
y/ˆ uˆ |
RP |
|
|
|
|
||||||||
Thus (ii) holds. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
R |
+ |
R |
|
(ii) = (iii) As R = |
|
obviously D is Hurwitz so (iii a) holds. Since |
|
RH∞, |
|
must |
|||||||||||
D |
RP |
RP |
|||||||||||||||
be proper. Since |
|
|
|
|
|
|
R |
|
|
NDP |
|
|
|
|
|
||
|
|
|
|
|
|
|
= |
|
, |
|
|
|
(13.6) |
||||
|
|
|
|
|
|
|
RP |
|
DNP |
|
|
|
|
||||
this implies that deg(DNP ) ≥ deg(NDP ). Since the degree of the product of polynomials is the sum of the degrees, it follows that
deg(D) + deg(NP ) ≥ deg(N) + deg(DP ),
from which (iii b) follows. If R, |
R |
RH |
+ |
+∞ it follows from (13.6) that all roots of NP |
in |
|
RP |
|
|||||
|
|
|
|
|
|
|
C+ must also be roots of N, and vice versa. Thus (iii c) holds.
(iii) = (i) Suppose that R has c.f.r. (N, D) satisfying the conditions of (iii). |
Let F be |
|
˜ |
˜ |
˜ |
the GCD of N and NP and write N = F N and NP = F NP . Then define P1 = DNP . Note
that by (iii a) and (iii c), P1 is Hurwitz. Now let P2 be an arbitrary Hurwitz polynomial having the property that deg(P1P2) = 2n − 1, where n = deg(DP ). By Corollary 13.5 we may find polynomials D and Nfb so that
|
D DP + NfbNP = P1P2. |
|
|
|
(13.7) |
˜ |
|
N |
|
Nfb |
|
We also take N = Dfb = NP2 |
. We now claim that if we take R = |
D |
and Rfb = |
Dfb |
, then |
the interconnection of Figure 13.14 is IBIBO stable. The relevant transfer functions that must be checked as belonging to RH+∞ are
T1 = |
RP R Rfb |
, |
T2 = |
RP R |
|
1 + RP R Rfb |
1 + RP R Rfb |
||||
|
|
|
|||
T3 = |
RP Rfb |
, |
T4 = |
R Rfb |
|
1 + RP R Rfb |
1 + RP R Rfb |
||||
T5 = |
RP |
, |
T6 = |
R |
|
1 + RP R Rfb |
1 + RP R Rfb |
Rfb
T7 = 1 + RP R Rfb .
NEED T3 and T7
To see that all of the transfer functions are have no poles in C+ first note that they can all be written as rational functions with denominator
˜ |
˜ |
2 |
(13.8) |
D DfbDP + N NfbNP = NP2 |
(D DP + NfbNP ) = NP1P2 . |
||
˜
P2 is Hurwitz by design, P1 is Hurwitz by (iii a) and (iii c), and N is Hurwitz by (iii c). Thus
all transfer functions T1 and T7 are analytic in C+.
Let us now give the numerator for each of the transfer functions T1 through T7 when put over the denominator (13.8), and use this to ascertain that these transfer functions are all

22/10/2004 |
13.3 Two controller configurations |
519 |
||||||||
|
|
|
|
|
|
|
|
|
˜ |
|
proper. In doing this, it will be helpful to have a bound on deg(NP2), which we now obtain. |
||||||||||
We suppose that deg(P1) = k so that deg(P2) = 2n − k − 1. Now, |
|
|||||||||
|
|
|
|
|
˜ |
|
|
|
|
|
|
|
deg(P1) = deg(D) + deg(NP ) |
|
|
||||||
|
|
= deg(D) + deg(NP ) − deg(F ) |
|
|||||||
|
|
≥ deg(DP ) + deg(N) − deg(F ) |
|
|||||||
|
|
˜ |
|
|
|
|
|
|||
|
|
= n + deg(N), |
|
|
|
|
|
|||
using (iii b). Therefore |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
˜ |
|
|
deg(P2) = 2n − 1 − deg(P1) ≤ 2n − 1 − n − deg(N) |
||||||||
|
= |
˜ |
|
|
|
|
(13.9) |
|||
|
deg(NP2) ≤ n − 1. |
|
|
|
|
|||||
Now we proceed with our calculations. |
|
|
|
|
|
|||||
1. |
|
|
|
|
˜ |
|
|
|
this gives |
|
T1: The numerator is NP N Nfb. Since N = NP2 |
|
|||||||||
|
|
T1 = |
NP Nfb |
. |
|
|
||||
|
|
|
|
|
||||||
|
|
|
|
|
P1P2 |
|
|
|
|
|
|
We have deg(P1P2) = 2n − 1 and deg(NP ) ≤ n. Since Nfb is obtained from (13.7), |
|||||||||
|
deg(Tfb) ≤ n − 1. From this we deduce that T1 |
is proper. |
|
|||||||
2. |
|
|
|
|
|
|
|
|
˜ |
|
T2: The numerator of T2 is NP N Dfb. Since N = NP2 this gives |
||||||||||
|
|
T2 = |
NP Dfb |
. |
|
(13.10) |
||||
|
|
|
|
|
P1P2 |
|
|
|
|
|
|
Again, deg(P1P2) = 2n − 1 and deg(NP ) ≤ n. In (13.9) we showed that deg(Dfb) ≤ |
|||||||||
3. |
n − 1, thus T2 is proper. |
|
|
|
|
|
||||
T3: The numerator of T3 is NP NfbD , giving |
|
|
|
|
|
|||||
|
|
T3 = |
NP NfbD |
|
|
|||||
|
|
|
|
|
||||||
|
|
|
|
|
˜ |
2 |
|
|
||
|
|
|
|
|
NP1P2 |
|
|
|||
|
We have deg(NP ) ≤ n and deg(P1P2) = 2n − 1. Since D |
and Nfb satisfy (13.7), |
||||||||
|
deg(D ), deg(Nfb) ≤ n − 1. |
|
|
|
|
finish |
||||
4. |
|
|
|
|
˜ |
|
|
|
this gives |
|
T4: The numerator is DP N Nfb. Since N = NP2 |
|
|||||||||
|
|
T4 = |
DP Nfb |
. |
|
|
||||
|
|
|
|
|
||||||
|
|
|
|
|
P1P2 |
|
|
|
|
|
|
We have deg(DP ) = n and deg(P1P2) = 2n − 1. Since Nfb satisfies (13.7), deg(Nfb) ≤ |
|||||||||
|
n − 1. This shows that T4 is proper. |
|
|
|
|
|
||||
5. |
|
|
|
|
˜ |
|
|
|
this gives |
|
T5: The numerator is NP D Dfb. Since Dfb = NP2 |
|
|||||||||
T5 = NP D .
P1P2
We have deg(DP ) = n and deg(P1P2) = 2n − 1. Since D satisfies (13.7), deg(D ) ≤ n − 1. This shows that T5 is proper.
520 |
13 Advanced synthesis, including PID synthesis |
22/10/2004 |
|||||
6. |
|
|
˜ |
|
|
this gives |
|
T6: The numerator is DP DfbN . Since N = NP2 |
|
||||||
|
T6 = |
DP Dfb |
. |
|
|
||
|
|
|
|
||||
|
|
|
P1P2 |
|
|
|
|
|
We have deg(DP ) = n and deg(P1P2) = 2n − 1. By (13.9) deg(Dfb) ≤ n − 1, showing |
||||||
|
that T6 is proper. |
|
|
|
|
||
7. |
T7: The numerator is DP D Nfb, giving |
|
|
|
|
||
|
T7 = |
DP D Nfb |
|
|
|||
|
|
|
|
||||
|
|
|
˜ |
2 |
|
|
|
|
|
|
NP1P2 |
|
|
||
|
We have deg(DP ) = n and deg(P1P2) = 2n − 1. |
Since D |
and Nfb satisfy (13.7) we |
||||
|
have deg(D ), deg(Nfb) ≤ n − 1. |
|
|
|
|
||
Finally we check that the closed-loop transfer function is R. Indeed, the closed-loop transfer function is T2 and we have
˜
N NNP
R = D = ˜ =
DNP
using (13.10).
Thus we have shown that the interconnection of Figure 13.14 is IBIBO stable with transfer
function R. This means that R is implementable. |
|
|||
13.22 Remarks 1. The conditions R, |
R |
|
+ |
|
|
RH∞ are actually the weakest possible for a |
|||
RP |
||||
class of interconnections more general than that of Figure 13.14. Indeed, if (S, G) is any interconnected SISO linear system with the property that every forward path from the reference rˆ to the output yˆ passes through the plant, then one readily sees that the
transfer function from the reference rˆ to the input uˆ to the plant is exactly |
R |
(cf. the |
|
||
|
RP |
|
proof that (i) implies (ii) in Theorem 13.21 below). Thus we have the following statement:
If (S, G) is an interconnected SISO linear system with the property that every forward path from the input to the output passes through the plant, then the
interconnection is IBIBO stable with transfer function R R(s) only if R, R
RP
RH+∞.
(This is Exercise E6.14.) This indicates that the conditions R, R RH+ are the weak-
RP ∞
est one can impose on a closed-loop transfer function if it is to be realisable by some “reasonable” interconnection. The additional hypothesis that R have no nonminimum phase zeros other than those of RP is reasonable: the nonminimum phase zeros of RP must appear in R, and we would not want any more of these than necessary, given the discussions of Chapters 8 and 9 concerning the e ects of nonminimum phase zeros.
2.As with our results of Section 13.2, Theorem 13.21 is constructive.
3.Note that the interconnection of Figure 13.14 is the same as that of Figure 10.9. Indeed, there is a relationship between the controllers constructed in Theorem 13.21 and the combination of the observer combined with static state feedback in Theorem 10.48. The procedure of Theorem 13.21 is a bit more flexible in that the order of the closed-loop characteristic polynomial is not necessarily 2n.
Let us first illustrate via an example that implementability is indeed di erent that stabilisation of the closed-loop system.

22/10/2004 |
13.4 Synthesis using controller parameterisation |
521 |
13.23 Example Let RP (s) = |
s2−2 |
. One can verify that R(s) = |
||||||
+ |
s |
−1 |
|
|
|
|
||
Indeed, clearly R RH∞ and we also have |
|
|
||||||
|
|
R(s) |
= |
|
1 − s2 |
RH+ . |
||
|
|
RP (s) s2 + 2s + 2 |
|
∞ |
||||
Since we have |
|
|
|
|
|
RC(s)RP (s) |
|
|
|
|
|
R(s) = |
|
, |
|||
|
|
|
1 + RC(s)RP (s) |
|||||
|
|
|
|
|
|
|||
we can solve this for RC to get
2 2−s |
is implementable. |
s +2s+2 |
|
RC(s) = |
R |
= |
|
1 − s2 |
. |
(R − 1)RP |
|
||||
|
|
s(s + 3) |
|||
Note that although R is implementable, the interconnection of Figure 13.8 is not IBIBO stable. Thus we see that implementability is di erent from an IBIBO interconnection of the
form Figure 13.8. |
|
13.3.2 Implementations that meet design considerations |
As we saw in Sec- |
tion 13.2.2, one often wants to enforce more than IBIBO stability on one’s feedback loop. Let us see how these considerations can be enforced in the two controller configuration of Figure 13.14.
13.4 Synthesis using controller parameterisation
In Section 10.3 we described the set of proper controllers that stabilise a proper plant RP , and the parameterisation came to us in terms of a free function in RH+∞. In this section we turn to using this parameterisation to provide a useful guide to controller design. We will be concerned with the standard plant/controller unity feedback loop, and we reproduce this in Figure 13.15 for easy reference.
rˆ(s) |
RC (s) |
RP (s) |
yˆ(s) |
|
− |
|
|
Figure 13.15 Interconnection for studying controller parameterisation
13.4.1 Properties of the Youla parameterisation We first recall the Youla parameterisation of Theorem 10.37. Given a proper plant RP , the set Spr(RP ) of proper controllers that render the interconnection of Figure 13.15 IBIBO stable is given by
|
|
Spr(RP ) = |
ρ1 |
+ θP2 |
|
θ admissible . |
|
|
|
||
|
|
ρ2 |
− |
θP1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Recall that (P |
, P |
) is a coprime fractional representative of R |
P |
and (ρ |
, ρ |
) is a coprime |
|||||
1 |
2 |
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
factorisation of (P1, P2). Also recall that the collection of admissible functions θ are defined by
522 |
|
|
|
|
|
|
13 Advanced synthesis, including PID synthesis |
22/10/2004 |
||
1. |
θ 6= |
ρ2 |
|
|
|
|
|
|
||
|
, and |
|
|
|
|
|||||
P1 |
|
|
6 |
|
||||||
2. |
s→∞ |
2 |
(s) |
− |
1 |
(s) |
|
|||
|
lim |
|
ρ |
|
θ(s)P |
= 0. |
|
|||
We wish to determine how the choice of the parameter θ a ects the properties of the closedloop system. For this purpose, let us suppose that we decide that we wish to place all poles of the closed-loop system in some region Cdes in the complex plane. Note that we can always do this, since by, for example, Theorem 10.27 or Theorem 13.2, we may construct controllers that achieve any closed-loop characteristic polynomial, provided it has su ciently high degree (twice the order of the plant for a strictly proper controller, and one less than this for a proper controller). Thus we are permitted to talk about the set of all proper controllers for which the closed-loop poles lie in Cdes, and let us denote this set of controllers by Spr(RP , Cdes). The following result describes these controllers using the Youla parameterisation.
13.24 Proposition Let RP be a proper plant and Cdes C be the set of desirable closed-loop pole locations. Also let (P1, P2) be a coprime fractional representative for RP with (ρ1, ρ2) a coprime factorisation of (P1, P2). Then
|
ρ1 |
+ θP2 |
|
|
|
Spr(RP , Cdes) = ρ2 |
− |
θP1 |
θ admissible and θ has all poles in Cdes . |
||
|
|
||||
|
|
|
|
|
|
Proof |
|
|
|
|
|
|
|
|
|||
The result is perhaps surprisingly “obvious,” at least in statement, and clearly provides a useful tool for controller design.
13.5Summary
1.Ziegler-Nichols tuning is available for doing PID control design.
Exercises for Chapter 13 523 524 13 Advanced synthesis, including PID synthesis 22/10/2004
|
Exercises |
|
|
|
rˆ(s) |
|
|
|
|
R (s) |
|
|
|
|
|
|
|
|
RP (s) |
|
|
|
yˆ(s) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
E13.1 |
In this exercise, you will show that the Ziegler-Nicols tuning method cannot be |
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
applied, even in some quite simple cases. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Nfb(s) |
|
|
|
|
|
|
||||||
|
(a) Show that for any first-order plant, say RP = s+b , both of the Ziegler-Nicols |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
methods will not yield PID parameter values. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dff(s) |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
(b) Show that there exists a second-order plant, say of the form RP (s) = |
a |
, so |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(a) |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
s2+bs+c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
that Assumption 13.1 will not be satisfied. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
E13.2 |
In this exercise, you will apply the Ziegler-Nicols tuning method to design PID |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
controllers for the plant transfer function |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
rˆ(s) |
|
|
|
|
|
Nff(s) |
|
|
|
|
|
|
|
|
|
|
Nfb(s) |
|
|
|
|
|
|
RP (s) |
|
|
|
yˆ(s) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
Nfb(s) |
|
|
|
|
|
|
|
|
|
|
Dff(s) |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
RP (s) = |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
s3 + s2 + 2s + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
First, the first method. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Nfb(s) |
|
|
|
|
|
|
||||||||
|
(a) Produce the step response numerically using Proposition 3.40. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Dff(s) |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
(b) Graphically (or with the computer, if you can) determine the values of σ and τ, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(b) |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
and so determine the parameters K, TI , and TD for the three cases of a P, PI, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
and PID controller. |
|
|
Figure E13.1 |
Alternate two controller configuration implementa- |
||||||||||||||||||||||||||||||||
|
(c) Using Proposition 3.40, determine the closed-loop step response. |
|
|
|
tions |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
(d)Comment on the performance of the three controllers. Now the second method.
(e)Verify that Assumption 13.1 is satisfied for the plant transfer function RP .
Hint: A good way to do this might be to use a computer package to solve the equation obtained by setting the real part of the poles to zero.
(f)Determine by trial and error (or with the computer, if you can) the value Ku of the proportional gain that makes two poles of the transfer function negative, and the period of the oscillatory part of the step response. Use these numbers to give the corresponding Ziegler-Nicols values for the parameters K, TI , and TD for the three cases of a P, PI, and PID controller.
(g)Using Proposition 3.40, determine the closed-loop step response.
(h)Comment on the performance of the three controllers.
E13.3 Exercises on controlling state examples using pole placement on output.
E13.4 Let RP be a proper plant and let R I (RP ). Suppose that the feedback and feedforward controllers giving R as the closed-loop transfer function in Figure 13.14 are Rfb and R , respectively. Let (N, D), (Nfb, Dfb), and (N , D ) be the c.f.r.’s for R, Rfb, and R , respectively.
(a)Show that all interconnections of Figure E13.1 have closed-loop transfer function R. Note that the recipe of Theorem 13.21 gives N = Dfb, so let us assume that this is the case.
(b)Show that the interconnection (a) of Figure E13.1 will not generally be IBIBO stable.
(c)Show that the interconnection (b) of Figure E13.1 will not generally be IBIBO stable.
