6.2. Метрологические характеристики средств измерений

Под метрологическими характеристиками (MX) понимают такие характеристики СИ, которые позволяют судить об их пригодности для измерений в известном диапазоне с известной точностью.

MX СИ вводят с целью:

- обеспечения возможности установления точности измерений;

- достижения взаимозаменяемости СИ, сравнения СИ между собой и выбора нужных СИ по точности и другим характеристикам;

- определения погрешностей измерительных систем и установок на основе MX входящих в них СИ;

- оценки технического состояния СИ при поверке.

На практике наиболее распространены статические и динамические MX, в зависимости от режима работы СИ.

Статический режим – это такой режим работы СИ, при котором изменением измеряемой величины за время, требуемое для проведения одного измерения, можно пренебречь.

В динамическом режиме такое пренебрежение недопустимо, поскольку указанное изменение превышает допустимую погрешность.

1. Статические МХ

Основной характеристикой СИ является функция преобразования – зависимость информативного параметра выходного сигнала Y от информативного параметра его входного сигнала X: Y = F( X ), где Y и X - истинные (при теоретическом анализе) и действительные (при экспериментальных исследованиях) значения выходной и входной величины.

Поскольку истинные значения величин не могут быть определены, то, соответственно, не может быть определена истинная функция преобразования. Можно определить лишь действительную функцию преобразования, принимая за Y и X некоторые их действительные значения.

Зависимость между выходным и входным сигналом СИ, полученную экспериментально, называют градуировочной характеристикой, которая может быть представлена аналитически, графически или в виде таблицы.

Коэффициентом преобразования называется отношение выходной величины Y к входной X:

K(X)=Y/X=F(X)/X, (6.1)

Диапазон измерений – область значений измеряемой величины, для которой нормированы допускаемые пределы погрешности СИ (для преобразователей – это диапазон преобразования).

Предел измерения – наибольшее или наименьшее значение диапазона измерения. Для мер – это номинальное значение воспроизводимой величины.

Цена деления шкалы – разность значений величин, соответствующих двум соседним отметкам шкалы. Приборы с равномерной шкалой имеют постоянную цену деления, а с неравномерной – переменную. В этом случае нормируется минимальная цена деления.

Чувствительность – отношение изменения сигнала Δy на выходе СИ к вызвавшему это изменение изменению Δx сигнала на входе

S = Δy / Δx, (6.2)

Поскольку х и у могут быть выражены в различных единицах, то величина S имеет размерность , ит.д.

Порог чувствительности – наименьшее значение измеряемой величины, вызывающее заметное изменение показаний прибора.

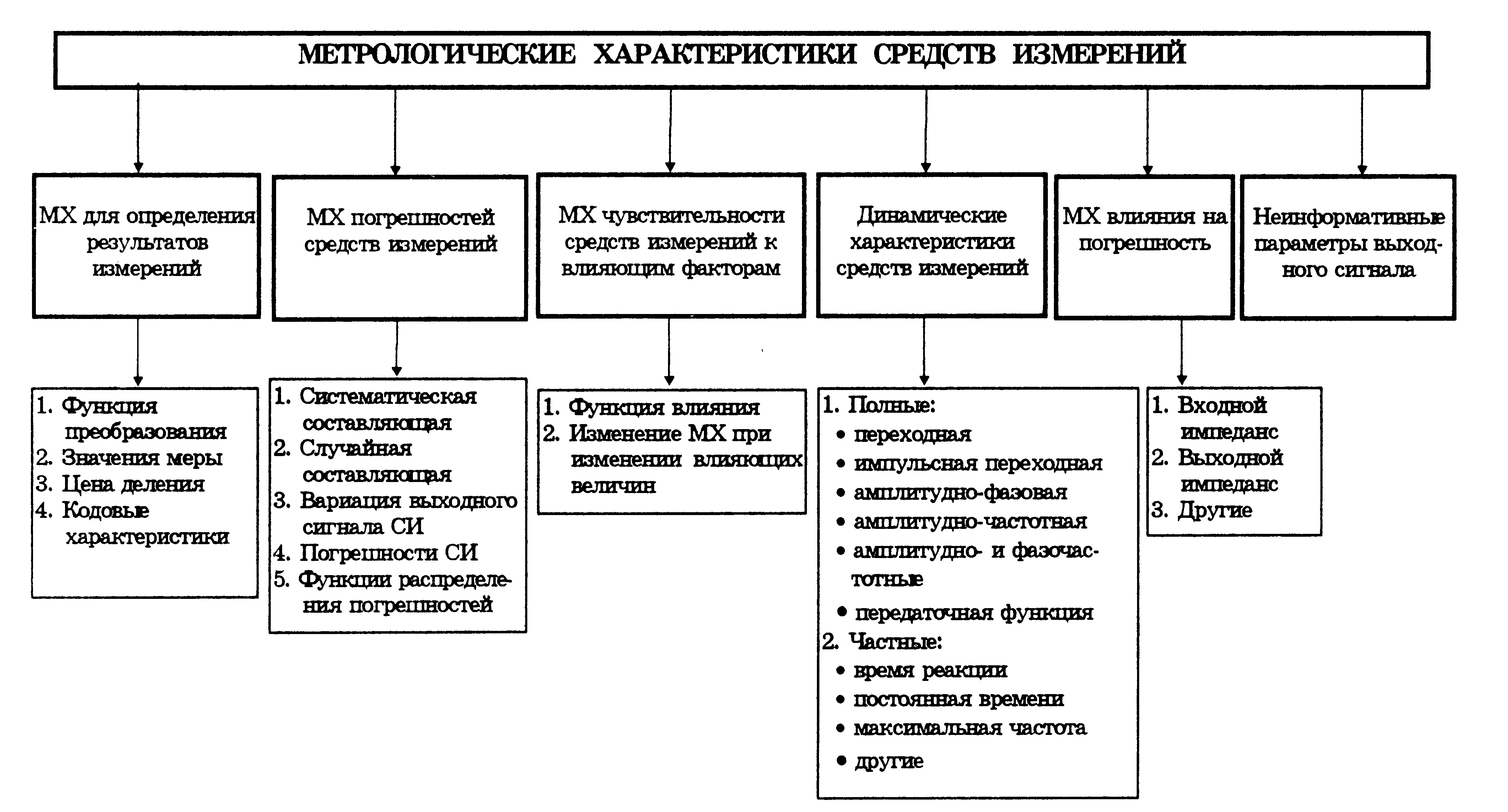
Рис.6.2. Номенклатура метрологических характеристик СИ

Вариация показаний– разность показаний СИ в одной и той же точке диапазона измерений при плавном подходе к ней со стороны меньших и больших значений измеряемой величины в неизменных внешних условиях

Основная MX СИ – погрешность СИ – есть разность между показаниями СИ и истинными (действительными) значениями ФВ.

Классификация погрешностей СИ приведена на рис. 6.3.

Все погрешности СИ в зависимости от внешних условий делятся на основные и дополнительные.

Основная погрешность – это погрешность СИ при нормальных условиях эксплуатации.

В рабочих условиях, зачастую отличающихся от нормальных более широким диапазоном влияющих величин, при необходимости нормируется дополнительная погрешность СИ. В качестве предела допускаемой погрешности выступает наибольшая погрешность, вызываемая изменением влияющей величины, при которой СИ по техническим требованиям может быть допущено к применению.

К характеристикам чувствительности средств измерений к влияющим величинам, то есть к влиянию, оказываемому внешними факторами, относят.

Функция влияния — это зависимость изменения MX средства измерений от изменения влияющей величины или их совокупности в рабочих условиях применения СИ. Использование функций влияния позволяет определить не предельно возможные значения погрешности, практически не встречающиеся при исправных СИ, а их статистические оценки. Нормирование функции производится путем установления ее номинального значения и преде­лов допустимых отклонений от него.

Изменения значений МХ СИ, вызванные изменениями влияющих величин в установленных пределах — это разность (без учета знака) между MX, соответствующей некоторому заданному значению влияющей величины в пределах рабочих условий применения СИ, и данной MX, соответствующей нормальному значению влияющей величины. Эти изменения нормируются путем установления пределов допускаемых изменений характеристики при изменении влияющей величины в заданных пределах.

В общем виде суммарная абсолютная погрешность СИ при влияющих факторах

, (6.3)

где Δ₀ – основная погрешность СИ; Δ_i – дополнительная погрешность, вызванная изменением i-го влияющего фактора.

Иногда дополнительную погрешность нормируют в виде коэффициента, указывающего, "насколько" или "во сколько" изменяется погрешность при отклонении номинального значения. Например, указание, что температурная погрешность вольтметра составляет ±1% на 10°С, означает, что при изменении среды на каждые 10°С добавляется дополнительная погрешность 1%

Вследствие сложности разделения дополнительных и основных погрешностей поверку СИ выполняют только при нормальных условиях (т. е. дополнительные погрешности исключены).

Систематическая погрешность СИ – это составляющая общей погрешности, которая остается постоянной или закономерно изменяется при многократных измерениях одной и той же величины.

Случайной погрешностью СИ называют составляющую, изменяющуюся при повторных измерениях одной и той же величины случайным образом.

Статические погрешности возникают при измерении постоянных величин после завершения переходных процессов в элементах СИ.

Абсолютная погрешность – разность между показанием СИ и действительным значением измеряемой величины.

. (6.4)

В качестве x_д выступает либо номинальное значение (например, меры), либо значение величины, измеренной более точным (не менее чем на порядок, в 10 раз) СИ.

Рис.6.3. Классификация погрешностей СИ

Поскольку абсолютная погрешность выражается в абсолютных единицах физической величины, то это не дает возможность сравнить СИ и измеряющие разные физические величины. Для этой цели можно использовать относительные погрешности δ как отношение абсолютной погрешности к действительному х_д значению, выраженные в процентах

. (6.5)

Указание только абсолютной погрешности не позволяет сравнивать между собой по точности СИ с разным пределом измерений, а указание относительной погрешности также ограничено из-за непостоянства величины δ. Поэтому получило большое распространение нормирование приведенной погрешности как отношение Δ к нормируемому значению х_N:

. (6.6)

Нормирующее значение х_N выбирают в зависимости от вида и характера шкалы прибора. Нормирующее значение принимается равным:

• конечному значению рабочей части шкалы;

• сумме конечных значений шкалы;

• длине шкалы, если она существенно неравномерна;

• номинальному значению х, если СИ предназначено для измерения отклонения измеряемой величины от номинального значения.

Специфическим видом погрешности цифровых СИ и дискретных преобразователей является погрешность квантования, которая вносится округлением значения измеряемой величины и номинального значения.

Наличие погрешностей приводит к тому, что характеристики СИ (датчиков, приборов, каналов ИИС и ИВК) оказываются неоднозначными. При экспериментальном их определении (градуирование СИ) находят некую среднюю линию. Тогда реальные отношения характеристик от этой аппроксимирующей являются погрешностью адекватности.

От рассеяния результата измерения следует отличать рассеяние показания СИ и рассеяние самой измеряемой величины, характеризующее однородность (стабильность) измерительного процесса. Последнее особенно важно учитывать при диагностических измерениях.

К МХ влияния на инструментальную составляющую погрешности измерения относятся характеристики СИ, отражающие их способность влиять на инструментальную составляющую вследствие взаимодействия СИ с любым из подключенных к его входу или выходу компонентов, например объектом измерений и др. Потребление энергии средством измерений от объекта измерения или от предвключенного прибора приводит к изменению значе­ния измеряемой величины и, следовательно, к появлению соответствующей составляющей погрешности. Следовательно, для СИ, работа которых характеризуется обменом энергией между ними и подключенными к их входу или выходу объектами, необходимо нормировать некоторые характеристики, описывающие свойства этих приборов отбирать или отдавать энергию через свои входные или выходные цепи. Такие характеристики часто называют импедансными, или просто импедансами.

2. Динамические МХ

Реальные СИ обладают инерционными (динамическими) свойствами, обусловленными особенностями используемых элементов. Это приводит к более сложной зависимости между входным и выходным сигналами.

В зависимости от полноты описания динамических свойств СИ различают полные и частные динамические характеристики.

Полная динамическая характеристика – характеристика, однозначно определяющая изменение выходного сигнала средства измерений при любом изменении во времени информативного или неинформативного параметра входного сигнала, влияющей величины или нагрузки. К полным динамическим характеристикам относят переходную характеристику, импульсную переходную характеристику, совокупность амплитудно-частотной и фазово-частотной характеристик, передаточную функцию.

Частная динамическая характеристика не отражает полностью динамических свойств СИ. К частным динамическим характеристикам аналоговых средств измерений, которые можно рассматривать как линейные, относят любые функционалы или параметры полных динамических характеристик. Примерами таких характеристик являются время реакции средства измерений, коэффициент демпфирования, значение резонансной собственной угловой частоты, значение амплитудно-частотной характеристики на резонансной частоте.

Динамический режим широкого класса средств измерений в том числе и измерительных преобразователей может быть описан линейным неоднородным дифференциальным уравнением с постоянными коэффициентами

AnYⁿ(t)+An­1Yⁿ‾¹(t)+...+A1Y´(t)+Y(t)=Kном.X(t). (6.7)

Члены уравнения, содержащие производные от выходного сигнала Y(t), определяют динамические свойства. Решение Y(t) дифференциального уравнения описывает выходной сигнал при входном воздействии X(t).

Погрешность в динамическом режиме представляет собой алгебраическую сумму динамической и статической погрешности. Поскольку статическая погрешность принята равной нулю, то рассматриваемая величина определяет только динамическую погрешность.

Переходная характеристика h(t) есть реакция СИ на входное воздействие X(t), представляющее собой единичный скачок 1(t). Она описывает инерционность ИС, обуславливающую запаздывание и искажение выходного сигнала относительно входного.

Импульсная переходная характеристика g(t) есть реакция ИС на входное воздействие в виде дельта-функции (t).

К частотным характеристикам относят амплитудно–фазовую, амплитудно–частотную и фазочастотную характеристики. Частотные методы анализа основаны на исследовании прохождения гармонических колебаний различных частот через СИ.

Используя преобразование Лапласа, отношение изображений выходного и входного сигналов

K(p)= Y(p)/X(p) = K_ном / (А_npⁿ+ А_n-1p^n-1+…+ А₁p +1), (6.8)

называют передаточной функцией. Передаточная функция является полной математической моделью средства измерений. Передаточную функцию можно представить в виде произведения

(6.9)

Таким образом, сложное средство измерений с передаточной функцией может быть представлено последовательным соединением простейших звеньев.