Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

KR_No2

.pdf

Скачиваний:

Добавлен:

31.05.2015

Размер:

651.18 Кб

Скачать

☆

1 / 71 2 3 4 5 6 7 > Следующая >>>

ФГБОУ ВПО ”Воронежский государственный технический университет”

Кафедра физики

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к решению задач и выполнению контрольной работы № 2 по физике для студентов всех технических направлений подготовки заочной сокращённой формы обучения

Воронеж 2012

Cоставители: канд. физ.–мат. наук А.Г. Москаленко, канд. техн. наук М.Н. Гаршина, канд. физ.-мат. наук И.А. Сафонов, канд. физ.-мат. наук Т.Л.Тураева

УДК 531 (07)

Методические указания к решению задач и выполнению контрольной работы № 2 по физике для студентов всех технических направлений подготовки заочной сокращённой формы обучения/ ФГБОУ ВПО “Воронежcкий государственный технический университет”; сост. А.Г. Москаленко, М.Н. Гаршина, И.А. Сафонов, Т.Л. Тураева. Воронеж, 2012. 62 с.

Методические указания содержат основные формулы, примеры решения задач, таблицы вариантов контрольных заданий по разделам: электростатика, постоянный электрический ток, электромагнетизм, колебания и волны.

Предназначены для студентов второго курса.

Методические указания подготовлены в электронном виде в текстовом редакторе MS Word 2003 и содержатся в файле Физика ЗО. КР №2.docx.

Табл. 4. Ил. 33. Библиогр.: 8 назв.

Рецензент д-р физ.-мат. наук, проф. Е.В. Шведов

Ответственный за выпуск зав. кафедрой канд. физ.-мат. наук, проф. Т.Л. Тураева

МЕТОДИЧЕСКИЕ УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ И ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ ПО ФИЗИКЕ ДЛЯ СТУДЕНТОВ ЗАОЧНОЙ СОКРАЩЁННОЙ ФОРМЫ ОБУЧЕНИЯ

1. Контрольные работы необходимо выполнять чернилами в школьной тетради, на обложке которой привести сведения по следующему образцу:

Контрольная работа №2 по физике студента ФВЗО, группы РК-031

Шифр251021 Иванова И.И.

2.Номера задач, которые студент должен включить в свою контрольную работу, определяются по таблице вариантов в соответствии с последним номером зачётной книжки (шифром).

3.Условия задач в контрольной работе надо переписывать полностью без сокращений.

4.Решение задач следует сопровождать краткими, но исчерпывающими пояснениями. В тех случаях, когда это возможно, даётся чертёж.

5.Решать задачу надо в общем виде, т.е. выразить искомую величину в буквенных обозначениях величин, заданных в условиях задачи.

6.Все вычисления следует проводить в единицах СИ с соблюдением правил приближённых вычислений.

7.Если контрольная работа при рецензировании не зачтена, студент обязан представить её на повторную рецензию, включив в неё те задачи, решение которых оказалось неверным.

КОНТРОЛЬНАЯ РАБОТА № 2

1.ЭЛЕКТРОСТАТИКА

1.1.Основные законы и формулы

1.Напряженность и потенциал поля точечного заряда

	1 q			1 q
E			r;			.
	4 0	r3		4 0	r

2. Принцип суперпозиции электростатических полей

n		n
E Ei ;		i
i	1	i 1

3.Линейная, поверхностная и объемная плотность зарядов dq dq dq

		;		;		.

dl ds dV

4. Теорема Гаусса для электростатического поля в вакууме

		1	N	1
ФE	EndS		qi		dV,
		0
			i 1	0 v

где qi – алгебраическая сумма зарядов, охватываемых поверхностью.

5. Связь между напряженностью и потенциалом электростатического поля

k ;

6.Циркуляция вектора напряженности

Eldl 0.

7.Работа сил электростатического поля

A12 q 1 2	1
A12 q 1 2	или A12 q Eldl.
	2
	2

8.Поляризованность диэлектрика

PPi / V,

i 1

где Pi – дипольный момент i-ой молекулы; V – объем диэлектрика.

Связь между поляризованностью диэлектрика и напряженностью электростатического поля

P 0 E ,

где – диэлектрическая восприимчивость вещества. 9. Вектор электрического смещения

D 0E P, или D 0E,

где = 1 + - диэлектрическая проницаемость вещества. 10. Теорема Гаусса для электростатического поля в

диэлектрике

ФD DndS qi,

S i 1

где qi – алгебраическая сумма сторонних электрических

i 1

зарядов, заключенных внутри замкнутой поверхности. 11. Условия на границе раздела двух диэлектриков

D2n D1n ;

E2 E1 .

12. Поле в однородном диэлектрике

E E0 / ;

D D0 ,

где E0 и D0 - напряженность и электрическое смещение внешнего поля.

13. Напряженность электрического поля у поверхности проводника

E / 0 ,

где – поверхностная плотность зарядов.

14.Электроемкость уединенного проводника и

конденсатора C q / ; C q / ( 1 2 ) . 15. Ёмкость плоского конденсатора

C 0 S / d ,

где S – площадь каждой пластины; d – расстояние между пластинами.

16. Емкость цилиндрического конденсатора

C 2 0 / ln(r2 / r1 ) ,

где	- длина обкладок конденсатора; r1 и r2 - радиусы
коаксиальных цилиндров .
	17. Емкость сферического конденсатора
			C 4			0	rr /(r r ),
							1		2	2	1
где r1 и r2 - радиусы концентрических сфер.
	18.	Емкость системы конденсаторов при последова-
тельном и параллельном соединении
		1		n	1					n
								; C Ci .
			C		Ci
				i 1						i 1
	19.	Энергия взаимодействия системы точечных зарядов
	i -			W			12 qi i				,
где		потенциал,		создаваемый						в той точке, где находится
заряд qi , всеми зарядами, кроме i – го.
	20.	Энергия системы с непрерывно распределенным
зарядом				W 12 dV.
	21.	Энергия заряженного конденсатора

W = CU2 / 2 = qU / 2 = q2 / 2C.

22. Объемная плотность энергии электростатического

поля

0 E2 . 2

1.2. Примеры решения задач

Пример 1. Два точечных электрических заряда Q1 = =1нКл и Q2 = - 2нКл находятся в воздухе на расстоянии d =10 см друг от друга. Определить напряжённость Е и потенциал φ поля, создаваемого этими зарядами в точке А, удалённой от заряда Q1 на расстоянии r1= 9 см и от заряда Q2 на r2= 7 см.

Решение

Согласно принципу суперпозиции электрических полей, каждый заряд создаёт поле независимо от присутствия в пространстве других зарядов. Напряжённость Е электростатического поля в искомой точке может быть найдена как

геометрическая сумма напряжённостей Е1 и Е2 полей,

создаваемых каждым зарядом в отдельности: Е Е1 Е2 .

Напряжённости электростатического поля, создаваемого в воздухе (ε = 1) зарядами Q1 и Q2,

Е1		Q1	(1),	Е2			Q2		(2).

	4 r2					4 r2
	0 1				0			2
				E1
			А	α					.
				α
			π-α					E
			π-α
			r1		E2
					E2
							r2
Q1			d					Q2
Q1			d					_
+
			5

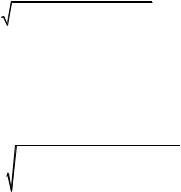
Вектор Е1 направлен по силовой линии от заряда Q1, так

как этот заряд положителен, вектор Е2 направлен также по

силовой линии, но к заряду Q2, так как этот заряд отрицателен. Модуль вектора Е найдём по теореме косинусов:

	E		E2 E2 2E E cos ,												(3)
			1				2		1	2
где α – угол между векторами							Е1		и Е2 , который может быть
найден из треугольника со сторонами r1, r2 и d
	cos				d		2 r		2 r2
							1			2	.
							2rr				.
							2rr
							1 2
Подставляя выражение Е1 из (1) и Е2													из (2) в (3), получим

Е	1			Q12		Q22		2		Q1			Q2	cos .	(4)


	4
	4	0		r4			r4			r2r2
		0	1				2			1		2

В соответствии с принципом суперпозиции электрических полей потенциал φ результирующего поля, равен алгебраической сумме потенциалов

1 2 . (5)

Потенциал электрического поля, создаваемого в вакууме точечным зарядом Q на расстоянии r от него, выражается формулой

(6)

4 0r

Согласно формулам (5) и (6) получим

, или

4 0r1

4 0r2

4 0

Произведём вычисления:

Е = 3,58 В/м,

φ = - 157 В.

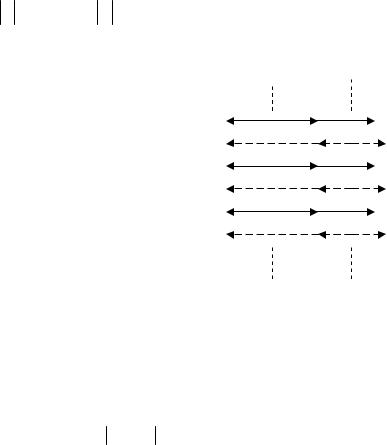
Пример 2. Электрическое поле создано двумя параллельными бесконечными заряженными плоскостями с поверхностными плотностями заряда σ1=0,4 мкКл/м2 и σ2=0,1мкКл/м2. Определить напряжённость электрического поля, созданного этими заряженными плоскостями.

Решение

Согласно принципа суперпозиции электростатических полей,

E E1 E2 ,

где, E1 12 0 и E2 22 0 - напряженности электростати-

ческих полей, создаваемых первой и второй плоскостями

соответственно.

III

Плоскости

делят

всё

прост-

σ1

σ2

ранство на три области: I, II, III.

Как видно из рисунка, в первой и

третьей

областях

электрические

силовые

линии

обоих

полей

направлены

одну

сторону и

следовательно,

напряжённости

суммарных полей Е(I) и Е(III) в

первой и третьей областях равны

между

собой,

противоположно

направлены

равны

сумме

напряжённостей полей, создавае-

мых первой и второй плоскостями:

( 1

E(I)

E(III) E E

или

E(I) E(III)

2 0

Во второй области (между плоскостями) электрические силовые линии направлены в противоположные стороны и, следовательно, напряжённость поля Е(II) равна разности напряжённостей полей, создаваемых первой и второй плоскостями: E(II) E1 E2 , или

E(II) ( 1 2) .

2 0

Подставив данные и произведя вычисления, получим

E(I) E(III) 28,3кВ/ м ,

E(II ) 17кВ/ м .

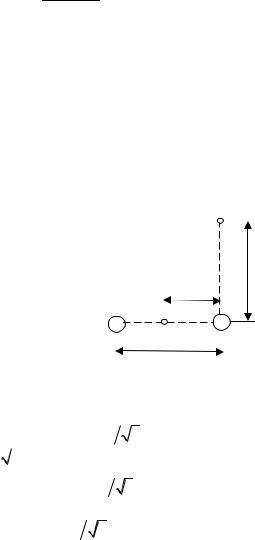
Пример 3. Электрическое поле создаётся двумя зарядами Q1 = 4 мкКл и Q2 = -2 мкКл, находящиеся на расстоянии a=0,1 м друг от друга. Определить работу А12 сил поля по перемещению заряда Q = 50 нКл из точки 1 в точку 2 (см. рис.).

Решение

Для определения работы А12

сил поля воспользуемся соотно-

шением

А12 Q( 1 2).

a/2

Применяя

принцип

супер-

позиции

электрических

полей,

определим

потенциалы

и 2

точек 1 и 2 поля:

2(Q1 Q2)

;

4 0a/2

4 0a

2 4 0a

4 0a

Тогда

(2(Q Q ) (Q

Q ) ,

4 0a

Или

2) Q

Q (2 1

4 0a

После подстановки численных значений, получим

A12 14,3мДж .

1 / 71 2 3 4 5 6 7 > Следующая >>>

Соседние файлы в папке физика

#
31.05.20151.23 Mб45EHlektrostatika._Postojannyi_tok._EHlektrodinamika._Magnetizm.pdf
#
31.05.20151.6 Mб52Kolebanija_i_volny.Optika._Kvantovaja_fizika._Fizika_jadra.pdf
#
31.05.2015651.18 Кб43KR_No2.pdf
#
31.05.2015513.84 Кб45KR_No3.pdf
#
31.05.20154.58 Mб151Teoreticheskaja_fizika.doc