Б) Двухполупериодные однофазные схемы выпрямления

Ход кривых тока при двухпериодном выпрямлении в схеме с нулевым выводом (рис.1.11,б) и мостовой схеме (рис.1.11,г) идентичны.

Вентильные токи, суммируясь в нагрузочном сопротивлении (R_d, X_d), дают выпрямленный ток Id . Как и в схеме однополупериодного выпрямления, вентильный ток к концу положительного полупериода не спадает до нуля, а сохраняет конечные значения за счет ЭДС самоиндукции индуктивности Ld. К моменту t= ток от одного вентиля (одних вентилей в мостовой схеме) переходит к другому (другим в мостовой схеме) в силу того, что напряжение в цепи первого вентиля становится отрицательным, в то время как напряжение в цепи второго вентиля – положительным.

Рис. 1.11. Двухполупериодное выпрямление в нулевой ( а,б) и мостовой схемах (в,г) при активно-индуктивной нагрузке

В переходе тока в момент t= от одной вторичной обмотки к другой в нулевой схеме или от одного полупериода выпрямления к другому и заключается основное отличие работы этих схем от схемы однополупериодного выпрямления.

Дифференциальное уравнение напряжений для однополупериодной схемы(рис.1.9)

,

из которого может быть определен ток в контуре, содержащем одну из вторичных обмоток трансформатора, активное сопротивление нагрузки Rd и индуктивное сопротивление , остается в силе и для двухполупериодных схем. Меняется лишь условие, по которому может быть найдена постоянная интегрирования А, определяющая начальное значение свободного тока . Для ее определения можно воспользоваться условием равенства значений выпрямленного тока в начале и в конце каждого из полупериодов

. (1.64)

Это приводит к уравнению

. (1.65)

Определяя А из (1.65) и подставляя его в полное уравнение для тока, находим

(1.66)

Это уравнение действительно в пределах углов от 0 до 

Вычисленные на основе (1.66) относительные значения выпрямленного тока в долях от максимального

в функции времени иллюстрируют кривые на рис.1.12.для разных значений .

Из кривых видно, что с ростом параметра (с удельным ростом индуктивного сопротивленияXd=Ld) пульсации в кривой тока заметно уменьшаются. Это говорит о том, что катодная индуктивность может быть успешно использована в схемах выпрямления с m=2 и выше в качестве сглаживающего звена-фильтра.

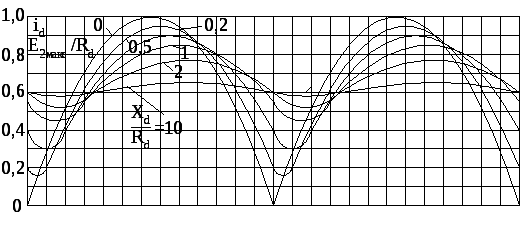
Рис. 1.12. Кривые выпрямленного тока в двухполупериодной схеме, работающей

на активно-индуктивную нагрузку при различных отношениях Х/R_d

Эффективность сглаживания пульсирующего тока повышается с увеличением числа пульсаций m, так как Xd=mLd растет пропорционально частоте пульсаций m за период.

Следует отметить преимущественное применение индуктивности в цепи нагрузки для преобразователей со значительными токами нагрузки, так как эффективность индуктивности определяется способностью запасать электромагнитную энергию в зависимости от протекающего по ней тока в квадратичной степени.

Поэтому наибольшее применение индуктивности в катодной (нагрузочной) цепи получило в выпрямителях средней и большой мощности. А в преобразователях для питания двигателей постоянного тока практически всегда в качестве фильтра применяются индуктивности в виде дросселей.