экзамен дм / 503680_7370C_otvety_na_bilety_po_dm_i_ok / шпоргалки / 9

Вопрос№9

4.2. Кинематические характеристики цилиндрических передач эвольвентного зацепления

1) Передаточное число. Передаточное число цилиндрических зубчатых передач определяется через отношение частот вращения или угловых скоростей, как для других типов передач, а также через отношение чисел зубьев колеса и шестерни:

.

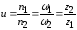2) Коэффициент перекрытия. Прямые зубья входят в зацепление и выходят из него сразу по всей длине, равной ширине зубчатого венца 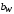. Для сохранения в каждый момент времени постоянства передаточного отношения необходимо, чтобы последующая пара зубьев вступала в зацепление до выхода из зацепления предыдущей пары зубьев. Следовательно, длина активной линии зацепления 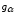должна быть не меньше основного шага 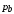– шага по основной окружности. В общем случае коэффициент торцевого перекрытия определяется по формуле:

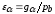> 1.

Теоретически коэффициент торцевого перекрытия может быть равен единице, т.е. в зацеплении всегда будет находиться одна пара зубьев. Но вследствие погрешностей изготовления, а также износа профилей зубьев в процессе эксплуатации, может оказаться, что коэффициент перекрытия будет меньше единицы. В данном случае будет нарушена плавность и непрерывность зацепления. Поэтому минимальное значение коэффициент торцевого перекрытия принимается равным .

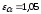Для цилиндрических передач, изготовленных без смещения, коэффициент торцевого перекрытия можно определить по приближенной формуле

,

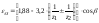где знак “+” – для внешнего зацепления; знак “–” для внутреннего зацепления.

Коэффициент перекрытия 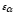увеличивается с уменьшением модуля зацепления и коэффициентов смещения 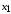и .

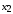В зацеплении цилиндрической передачи с прямыми зубьями может находиться или одна или две пары зубьев, т.е. реализуется однопарное или двухпарное зацепление. Зона однопарного зацепления располагается в районе полюса зацепления. В данный момент времени зуб передает полную нагрузку. Именно поэтому расчет на контактную выносливость проводится для случая, когда текущая точка контакта зубьев располагается в полюсе зацепления.

Вследствие того, что в зацеплении находится попеременно одна или две пары зубьев, постоянно изменяется суммарная жесткость зацепления. Это в свою очередь ведет к возникновению параметрических колебаний с зубцовой частотой

,

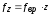где 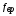– частота вращения вала зубчатого колеса, Гц; – число зубьев колеса.

Вследствие наклона зубьев в цилиндрических косозубых передачах, перекрытие работы зубьев наблюдается, как в осевой, так и в торцевой плоскости. В данном случае коэффициент перекрытия складывается из двух величин:

,

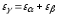где 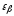– коэффициент осевого перекрытия.

Коэффициент осевого перекрытия определяется по формуле:

,

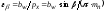где 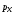– осевой шаг.

В прямозубом зацеплении нагрузка передается мгновенно. Это явление сопровождается ударами и шумом. В зависимости от соотношения накопленной погрешности шага и деформации зубьев под нагрузкой может происходить срединный или кромочный удар.

В косозубых передачах зубья входят в зацепление не сразу по всей длине, как в прямозубых передачах, а постепенно. Поэтому зубья нагружаются также постепенно, и передача работает плавно с меньшим шумом и динамическими нагрузками. Кроме того, в зацеплении находится минимум две пары зубьев. Следовательно, при тех же габаритах повышается нагрузочная способность передачи.

3) Скольжение и трение в зацеплении. В точках контакта С наблюдается перекатывание и скольжение зубьев. Скорость скольжения можно определить методом обращенного движения, который заключается в следующем. Всей системе сообщается угловая скорость, равная по модулю, например, угловой скорости шестерни, но направленная в противоположную сторону (рис. 4.4). В результате шестерня останавливается, а колесо будет вращаться вокруг полюса зацепления Р как мгновенного центра скоростей с угловой скоростью 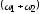. Тогда скорость относительного движения (скорость скольжения) в текущей точке контакта зубьев будет определяться выражением

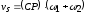. (4.11)

В соответствии с выражением (4.11) скорость скольжения прямо пропорциональна расстоянию между текущей точкой контакта зубьев и полюсом зацепления. В полюсе зацепления она равна нулю, а при переходе через него меняет знак. Следовательно, максимальное скольжение наблюдается на ножках и головках зубьев. Скольжение сопровождается трением, которое, в свою очередь, является причиной потери мощности в зацеплении и износа зубьев.

При постоянных диаметрах зубчатых колес расстояние от точек начала и конца зацепления данной пары зубьев до полюса зацепления, а, следовательно, и скорость скольжения увеличиваются с увеличением высоты зуба и модуля зацепления. Поэтому в мелкомодульных зубчатых передачах с большим числом зубьев и меньшими их размерами, скольжение меньше, а КПД выше по сравнению с крупномодульными передачами с малым числом зубьев и большими их размерами.