Вопрос№7

3.3. Требования, предъявляемые к зубчатым передачам

К зубчатым передачам предъявляются следующие требования.

1) Постоянство передаточного отношения – основное требование, предъявляемое к зубчатым передачам.

Этому требованию удовлетворяют две взаимоогибаемые кривые, образующая нормаль к которым в текущей точке касания С проходит через полюс зацепления Р, не меняющий на линии центров О₁О₂ своего положения (рис. 3.3). Передаточное отношение в данном случае определяется следующими выражениями:

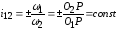; . (3.1)

Зависимости (3.1) являются математической записью основной теоремы зацепления, которая звучит следующим образом: нормаль в точке касания элементов высшей пары качения и скольжения делит линию центров на части, обратно пропорциональные угловым скоростям.

2) Простота образования профилей зубьев при изготовлении.

3) Взаимозаменяемость колес.

4) Возможность изменения межосевого расстояния без изменения передаточного отношения.

5) Минимальный износ.

6) Плавность и бесшумность работы.

3.4. Сравнительная оценка зубчатых зацеплений

3.4.1. Эвольвентное зацепление

Первым четырем требованиям, предъявляемым к зубчатым передачам (см. подразд. 3.3), наиболее полно удовлетворяет эвольвента окружности. Эвольвента окружности представляет собой кривую, описываемую любой точкой производящей прямой при ее перекатывании без скольжения по основной окружности радиуса(рис. 3.4).

Линия зацепления – геометрическое место точек контакта профилей зубьев при обкате.

Линия зацепления для рассматриваемого случая представляет собой прямую линию, что обеспечивает эвольвентному зацеплению существенные преимущества перед другими видами зацепления. Линия зацепления является нормальной к рабочим профилям зубьев в текущей точке контакта. По ней направлена сила в зацеплении. При перекатывании зубьев угол зацепления остается неизменным, не меняется положение линии зацепления, а, следовательно, нагрузки на валы и опоры остаются постоянными. Данный факт является существенным преимуществом по сравнению с циклоидальным зацеплением.

Линия зацепления является касательной к основным окружностям с радиусами и. Различают теоретическую() и активную линии зацепления. Активная линия зацепления представляет собой фактическое геометрическое место точек контакта профилей зубьев. Она получается пересечением линии зацепления с окружностями вершин зубьев шестерни и колеса. В крайних точках активной линии зацепления происходит вход и выход из зацепления данной пары зубьев.

Начальные окружности – это окружности, которые перекатываются друг по другу без скольжения. Контакт начальных окружностей происходит в полюсе зацепления P, положение которого на линии центров определяется передаточным отношением.

Между радиусами иосновных и начальных окружностей существует следующая зависимость:

; ,

тогда

.

Таким образом, передаточное отношение не зависит от угла зацепления , а зависит только от радиусов основных окружностей. Поэтому, изменяя межосевое расстояние, изменяются угол зацепления и радиусы начальных окружностей, радиусы основных окружностей остаются неизменными, следовательно

.

Данное свойство эвольвентного зацепления позволяет нарезать зубчатые колеса со смещением, т.е. проводить модификацию рабочих профилей зубьев, которая обеспечивает улучшение качественных показателей передачи:

– повышение изгибной и контактной прочности;

– уменьшение износа и повышение стойкости к заеданию;

– повышение плавности работы передачи.