Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Иркутский государственный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

mopg[1]

.pdf

Скачиваний:

Добавлен:

31.05.2015

Размер:

438.45 Кб

Скачать

☆

<<< < Предыдущая 12 / 32 3 > Следующая >>>

нованиям, заключенными между ее боковыми сторонами, равен среднему гармоническому оснований трапеции.

Решение.

Пусть

ABCD

(AD || BC)

данная трапеция,

AD = b , BC = a (b > a).

Пусть, далее O - точка

пересечения

диагоналей

тра-

пеции и прямая, проходящая

через

точку

параллельно

основаниям пересекает боко-

вые

стороны

трапеции

Рис. 16

AB иCD в точках M иN со-

ответственно (рис.16).

2ab

Требуется доказать, что MN =

a +b

Из подобия треугольников

BOC и

DOA, заключаем, что

поэтому

Из

подобия

тре-

a +b

угольников

MBO

ABD

(AD || MO)

получаем

и, следовательно,

a +b

MO =

(11).

a +b

OCN и

ACD

Аналогично, из подобия

треугольников

(ON ||

AD) получаем, что

OС

a +b

ON =

(12)

a +b

Из равенства (11) и (12 ) заключаем, во-первых, что

MO = ON , во-вторых, что MN = MO +ON = a2+abb .

Что и требовалось доказать.

Задача 1.16. Доказать, что если трапеция разделена прямой, параллельной её основаниям, на две подобные трапеции, то отрезок этой прямой, заключённый между боковыми сторонами, равен среднему геометрическому ее оснований.

Решение.

Пусть

ABCD

(AD || BC) данная трапеция, EF||AD,

причем

трапеция

EBCF

подобна

трапеции AEFD (рис. 17). Тогда

EF = BC AD .

Рис. 17

то есть

Что и требовалось доказать.

Задача 1.17.

Трапеция разделена прямой, параллельной

её основаниям, равным а и b, на две равновеликие трапеции.

Найти

длину отрезка этой

прямой, заключённый между боко-

выми сторонами.

Решение.

Пусть

ABCD

(AD || BC)

данная

трапеция,

AD = b , BC = a (b > a). MP||AD, причем

MBCP

ABCD

(13)

Проведем BH AD,

BE || CD и обозначим точки пересе-

чения BH и BE с MP через K и

N соответственно (рис. 18). То-

гда условие (13) можно записать

виде

MP + BC

BK =

AD + BC

или

Рис. 18

a +b

(14)

2(MP + a)

Из подобия треугольников ABE и MBN следует, что

или

MP −a

. Сравнивая последнее равенство

b −a

с (14),

получаем, 2(MP

−a

) = b

−a

, или MP =

+b2

Ответ:

Замечания.

1.Выражение

+b2

называется средним квадратичным

(квадратическим) чисел а и b .

2. Используя утверждения задач 1.15, 1.16 и 1.17, а также

свойство средней линии трапеции, можно доказать неравенство между средними двух положительных чисел:

min(a,b) ≤	2ab		≤ ab ≤	a +b	≤	a2 +b2	≤ max(a,b) .
	a	+b		2		2

Равенство возможно только в случае а=b.

Задача 1.18. Найти длину отрезка, отсекаемого диагоналями трапеции на средней линии, если основания трапеции равны a иb .

Решение. Пусть дана трапе-
ция ABCD		(AD \|\| BC),		AD = b ,		B		C
BC = a	и	для	определенности

b > a .	MN -	средняя линия трапе-			M			N
ции, M AB ; N DC . Обозначим						P	Q

точки пересечения			MN с диагона-		А			D
лями трапеции AС и BD через P и						Рис. 19
Q соответственно (рис. 19).
Рассмотрим			ABD .	Так как


AM = MB и MQ \|\|						AD , то MQ - средняя линия ABD и, следова-
тельно MQ =			1		AD =		1	b .
			2
						2
Аналогично,						MP - средняя линия ABC и, следовательно
MP =	1	BC =		1	a .

2			2

Получаем PQ = MQ − MP = 12 b − 12 a = b −2 a .

Отметим, что если a > b , то очевидно, PQ = a −2 b .

Таким образом PQ = a −2 b .

Ответ: a −2 b .

Методическое замечание

Как правило, при построении чертежа изображают трапецию, у которой оба угла при нижнем основании – острые. У трапеции, изображенной на рисунке 19, один из углов при нижнем основании – тупой. В некоторых задачах этот факт может играть важную роль (см., например, задачи 51 - 53).

Задача 1.19. Доказать, что для любой трапеции точка пересечения диагоналей, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой.

Решение. Пусть диагонали АС и BD трапеции ABCD пересекаются в точке Р, а продолжения боковых сторон АВ и CD — в точке Q (рис. 20 ).

Через середину М основания ВС и точку Р проведём прямую. Пусть она пересекает основание AD в точке N. Тогда треугольник BMP подобен треугольнику DNP, а треугольник СМР

— треугольнику ANP, причём в обоих случаях коэффициент по-

добия равен	MP . Значит
	PN
BM =MP =		CM , и так как BM=CM, то DN=AN. То есть N
DN	PN	AN
– середина AD.					Q
Следовательно, отрезок, со-					Q
Следовательно, отрезок, со-
единяющий	середины оснований
трапеции, проходит через точку
пересечения диагоналей.
Аналогично из подобия тре-			В	M	С
угольников AQN и BQM, NQD и			В	M	С
угольников AQN и BQM, NQD и
MQC доказывается, что прямая,					P
проведённая через середины ос-					P
проведённая через середины ос-
нований трапеции, проходит через				N	D
точку пересечения Q продолжений А				N	D
боковых сторон.		Следовательно,	Рис.20
точки Р, Q и середины оснований			Рис.20
точки Р, Q и середины оснований

трапеции лежат на одной прямой. Что и требовалось доказать.

Задача 1.20. Доказать, что если сумма углов при одном из оснований трапеции равна 90°, то отрезок, соединяющий середины оснований трапеции, равен их полу разности.

Решение. Пусть в трапеции ABCD (AD||BC) сумма углов

при основании АD равна 90°, М				P
– середина ВС, N – середина AD,				P
Р – точка пересечения продол-		B			C
жений боковых сторон трапеции			M
(рис. 21). Точки P, M и N лежат	A	N			D
на одной прямой (задача 1.19).		N	Рис. 21
Из условия задачи следует,			Рис. 21
Из условия задачи следует,

что угол APD – прямой; PN=0,5AD, PM=0,5BC (утверждение 1.3). Следовательно, MN=PN-PM=0,5(AD-BC), что и требовалось доказать.

Выпуклые четырехугольники

Задача 1.21. Доказать, что четырехугольник, вершинами которого являются середины сторон выпуклого четырехугольника является параллелограммом и вычислить его площадь, если площадь данного четырехугольника равна S .

Решение. Пусть дан четырехугольник ABCD , M , N, P,Q - середины сторон AB, BC, CD, DA соответственно (рис. 22).

Проведем диагонали

AС

BD тогда

MN -

средняя линия

ABC ,

поэтому

MN ||

MN =

AC ;

QP -

средняя линия

QP ||

ACD ,

поэтому

Рис. 22

QP =

AC .

Следовательно,

MN || QP и MN = QP и по признаку параллелограмма MNPQ -

параллелограмм. Вычислим его площадь.

SMBN

MBN ~

ABC и

следовательно,

т.е.

S ABC

SMBN = 14 S ABC .

Аналогично, SPQD = 14 S ADC , SMAQ = 14 S ABD , SNCP = 14 SBCD .

SMBN + SPQD + SMAQ + SNCP = 14 (SABC + SADC + SABD + SBCD )= = 12 SABCD = 12 S.

Следовательно, SMNPQ = 12 S . Что и требовалось доказать.

II Окружности, связанные с треугольником и четырехугольником

Вписанная окружность

Окружность называется вписанной в выпуклый многоугольник, если она касается всех его сторон. В курсе планиметрии доказываются следующие утверждения:

Утверждение 2.1. В любой треугольник можно вписать окружность и притом только одну. Центром окружности, вписанной в треугольник, является точка пересечения биссектрис треугольника.

Утверждение 2.2. В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.

В частности, из всех параллелограммов только в ромб можно вписать окружность.

Утверждение 2.3. Если в выпуклый четырехугольник можно вписать окружность, то биссектрисы всех его внутренних углов пересекаются в одной точке, являющейся центром вписанной окружности.

Утверждение 2.4. Радиус окружности, вписанной в вы-

пуклый многоугольник можно вычислить по формуле r = Sp , где

S –площадь многоугольника, р - его полупериметр.

Задача 2.1. В треугольнике АВС АВ=с, ВС=а, АС=b. Найти длины отрезков, на которые вписанная окружность делит сторону АС.

Решение. Пусть D, E и F-точки

касания окружности со			сторонами
треугольника АВ, ВС и АС соответст-
венно (рис. 23). Найдем длины отрез-
ков AF и FC. По свойству касатель-
ных к окружности получаем AD=AF, А
BE=BD,		CE=CF.	Поэтому
a +b +c = 2AF +2a или
AF =	a +b +c	−a . Обозначим через p

2				АВС,
полупериметр		треугольника

FС =b − AF = p −c. Ответ: p – a, p – c.

D E

Рис. 23

тогда AF=p-a.

Замечание. Очевидно, что сторона АВ делится точкой касания вписанной окружности на отрезки длиной p – a, p – b, а сторона ВС – на отрезки длиной p – b, p – c.

Задача 2.2. Доказать, что в прямо-	A
угольном треугольнике периметр равен
сумме двух диаметров описанной окруж-
ности и двух радиусов вписанной окруж-			D
ности.	F
	F
Решение: Пусть D, E и F- точки ка-	C	E	B
сания окружности со сторонами треуголь-		E	Рис. 24
сания окружности со сторонами треуголь-
ника АВ, ВС и АС соответственно (рис. 24).
Тогда CЕ=СF=r, где r – радиус вписанной
окружности, АВ=2R, где R – радиус описанной окружности. По-
лучаем
a +b +c = 2CE +2(DB + AD) = 2r +2AB = 2r +4R ,			что и
требовалось доказать.

Замечание. Из условия задачи следует, в частности, что радиус окружности, вписанной в прямоугольный треугольник

можно вычислить по формуле r = a +2b −c .

Задача 2.3. Вычислить радиус окружности, вписанной в треугольник, если известны длины его высот ha, hb и hc.

Решение. Пусть дан треугольник АВС, ha, hb, hc – высоты, опущенные на стороны ВС, АС и АВ соответственно. Обозначим через r радиус вписанной окружности, тогда для вычисления площади треугольника АВС справедливы следующие формулы:

S = 12 BC ha , S = 12 AC hb , S = 12 (AB + BC + AC) r

Выразим из первых трех равенств ВС, АС и АВ соответственно и подставим в последнее равенство, получим:

	1	2S		2S		2S
S =	1	2S	+	2S	+	2S	r	или
S =	2	h	+	h	+	h	r	или
		c		a		b

(15)

Из формулы (15) можно получить искомое

значение ра-

диуса.

Ответ:

Методическое замечание

Для решения задачи 2.3 нет необходимости в построении чертежа, требуемый результат получается алгебраическим методом. Этот метод заключается в том, что для определения геометрических величин составляется система уравнений, как правило, содержащая столько уравнений, каково количество неизвестных величин.

Задача 2.4.	В трапецию ABCD (AD \|\| BС) вписана ок-
ружность с центром в точке O . Доказать, что треугольники OBA
и OCD - прямоугольные.
Решение. Докажем, что							B		C
Решение. Докажем, что
BOA = 90o .
Так как по условию задачи								O
O - центр вписанной в трапе-								O
цию окружности, то AO и BO -
биссектрисы углов BAD и CBA			A						D
соответственно (рис. 25).			A						D
соответственно (рис. 25).							Рис. 25
Поэтому:							Рис. 25
1	1		1		o		o
OBA + BAO = 2	CBA + 2 BAD =		2	180		= 90		B	C
Так как						Е
BOA =180o −( OBA + BAO),						Е
BOA =180o −( OBA + BAO),								O
то BOA = 90o ,	следовательно,							O
треугольник OBA - прямоуголь-
ный.			A						D
Аналогично	можно	дока-	A					Рис. 26	D
зать, что COD = 90o и		тре-						Рис. 26
угольник OCD - прямоугольный.

Задача 2.5. Вычислить радиус окружности, вписанной в трапецию, если точка касания окружности делит боковую сторону трапеции на отрезки длинной p и q.

Решение. Пусть дана трапеция ABCD (AD || BС) и в нее

вписана окружность с центром в точке O , которая касается боковой стороны АВ в точке Е, AE=p, EB=q (рис. 26). Как доказано выше (задача 2.4) угол АОВ прямой и ОЕ – высота, опущенная из вершины прямого угла. По свойству высоты (утверждение

1.5) получаем OE = pq . Ответ: pq .

Описанная окружность

Окружность называется описанной около выпуклого многоугольника, если на ней лежат все его вершины.

Перечислим основные утверждения, связанные с описанной окружностью:

Утверждение 2.5. Вокруг любого треугольника можно описать окружность и притом только одну.

Утверждение 2.6. Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров. При этом для остроугольного треугольника эта точка находится внутри треугольника, для тупоугольного треугольника – за пределами треугольника.

Центром окружности, описанной вокруг прямоугольного треугольника, является середина гипотенузы.

Утверждение 2.7. Радиус окружности, описанной около

треугольника АВС,		АВ=с, ВС=а, АС=b можно вычислить по
одной из следующих формул:
R =		a	(следствие из теоремы синусов) (16)
	2sin A

= abc

R (17) 4S

где S – площадь треугольника АВС.

Утверждение 2.8. Если вокруг выпуклого многоугольника можно описать окружность, то серединные перпендикуляры к его сторонам пересекаются в одной точке, которая является центром описанной окружности.

Утверждение 2.9. Вокруг выпуклого треугольника можно описать окружность тогда и только тогда, когда сумма его двух противоположных углов равна 180°.

В частности, из всех параллелограммов только вокруг прямоугольника можно описать окружность и только вокруг равнобокой трапеции можно описать окружность.

Утверждение 2.10. Если четырехугольник ABCD вписанный, то AB · CD + AD · BC = AC · BD (теорема Птолемея).

Утверждение 2.11. Противоположные стороны вписанного четырехугольника антипараллельны относительно двух других его сторон, а диагонали вписанного четырехугольника антипарраллельны относительно любой пары его противоположных сторон.

Задача 2.6. Биссектриса СС1 пересекает описанную окружность треугольника АВС в точке P. Доказать, что

a)точка P является серединой дуги АРВ;

b)треугольники POB и POA равно-

бедренные, где О – центр вписанной ок-		C
ружности треугольника АВС;
c) Р – центр описанной окружно-
сти треугольника АОВ.		O
Решение. а) Первое утверждение		O
Решение. а) Первое утверждение
задачи следует из равенства углов АСР и	A		B
РСВ и теоремы об измерении вписанных	A	C1	B
углов (рис. 27).		P Рис. 27
b) Отметим, что точка О – центр		P Рис. 27

вписанной окружности лежит на биссектрисе СС1. Так как угол С1ОВ является внешним углом тре-

угольника СОВ, а угол С1ОА- внешний угол треугольника AOC, то


СOB = OBC + OCB =		1	( C + B) =90o − A		(18)

1	2			2

СOА= OСС+ OАА =	1		( C + А) =90o	− В .	(19)

1	2			2

Далее, РАB = РСB как вписанные углы, опирающиеся на одну и ту же дугу РВ. Аналогично РВА= РСА. Поэтому

РВО = РСА+ АВО = 12 ( С + В) =90o − 2А

РАО = РСВ+ ВАО = 12 ( С + А) =90o − 2В .

Сравнивая последние равенства с (18) и (19) соответственно, получаем, что РВО = РОB и РАО = РОА, то есть треугольники POB и POA равнобедренные.

Утверждение с) задачи является прямым следствием утверждения b), так как РА=РО=РВ.

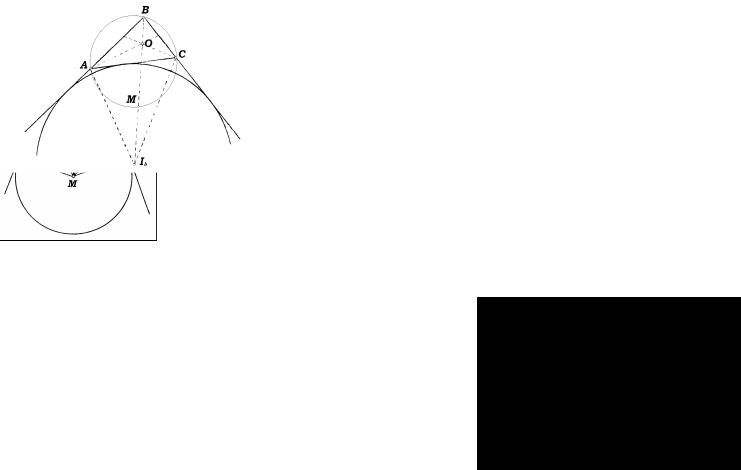
Задача 2.7. Биссектриса угла С треугольника АВС пересекает описанную окружность этого треугольника в точке P. О1 и О2 - центры вписанной и описанной окружностей треугольни-

ка АВС соответственно, а r и R -

ра-

диусы этих окружностей.

доказать, что СO1 O1P = 2rR ;

доказать, что

O1O2=

−2rR (теорема Эйлера).

O2O

Решение.

Проведем

O1E CB , О1Е=r, и диаметр DB опи-

санной окружности, DB=2R (рис. 28).

Рис. 28

Так как

PCB = РDB как вписанные углы, опирающиеся на

одну и ту же дугу,

и CEO = DPB =90o , то треугольники

CO1

EO1

О1EC и BPD подобны. Поэтому

или CO1 PB = 2Rr .

Так как треугольник PO1B –

равно-

бедренный

(задача

2.7),

то

CO1 PB =CO1 OP1 = 2Rr ,

что

тре-

бовалось доказать.

O2о о O1

2) Проведем диаметр DЕ опи-

санной окружности, проходящий че-

рез центр O1

вписанной окружности

(рис. 29). Используя теорему о про-

Рис. 29

порциональных отрезках хорд и касательных к окружности, получаем DO1 O1E =CO1 O1P или (R +O1O2 ) (R −O1O2 )= 2Rr . Вы-

ражая из последнего равенства O1O2, получаем O1O2= R2 −2rR . Что и требовалось доказать

Задача 2.8. Около остроугольного треугольника АВС описана окружность. Известно, что на этой окружности лежит центр другой окружности, проходящей через вершины A, C и точку пересечения высот треугольника ABC. Найдите угол ABC.

Решение. Если Е — точка пересе-						B
чения	высот	треугольника	ABC,	то

AЕC = 180o - ABC (рис. 30). Тогда
	AOC = AЕC = 360o - 2 AЕC =					E
2 ABC,					A
где O — центр второй окружности.

Поскольку AOC + ABC = 180o,						C
то 3 ABC = 180o.					O
Следовательно, ABC = 60o.						Рис. 30

Ответ: 60o.

Задача 2.9. Пусть BM и CN – высоты треугольника АВС, O –центр описанной около этого треугольника окружности. Доказать, что AO MN .

Решение: Рассмотрим случай, когда треугольник АВС –


остроугольный. Проведем диаметр AD,						А
ABD = 90o . Обозначим через Е точку						А
ABD = 90o . Обозначим через Е точку
пересечения AD и MN (рис. 31). Прямые						M Е
MN и	CB	антипараллельны относи-				M Е	N
тельно прямых АС и АВ (см. замечание						O
к	задаче		1.10),	поэтому	C		B
ANM		= ACB . С		другой сто-	C		B
роны,	ACB = ADB как			вписанные		D
углы, опирающиеся на одну и ту же ду-						Рис. 31
гу, поэтому			ANM = ADB . Кроме

того у треугольников ABD и AEN угол при вершине А – общий,

поэтому AEN = ABD =90o . Что и требовалось доказать. Замечание. Случаи, когда один из углов треугольника ту-

пой рассматриваются аналогично.

Задача 2.10. Известно, что в трапецию можно вписать окружность и вокруг трапеции можно описать окружность. Найти радиусы этих окружностей, если основания трапеции равны a и b.

Решение. Пусть дана трапеция

АВСD (BC||AD), BC=a, AD=b (b>a).

Так как вокруг трапеции описана ок-

ружность, то AB=CD (рис. 32). Так как

в трапецию можно вписать окружность,

то ВС+АD=2AB,

то

есть

AB =

a +b

Рис. 32

b −a

Проведем

BH AD,

AН =

(задача

1.13).

Вычислим высоту трапеции

a +b

b −a

BH =

− AH

−

= ab .

Так как высота трапеции равна диаметру вписанной окружности, то получаем формулу для вычисления радиуса впи-

санной окружности r =	ab	.
	2

Окружность, описанная около данной трапеции, является описанной для треугольника ABD. Для вычисления ее радиуса воспользуемся следствием из теоремы синусов (16). Имеем:

BD = BH

+ DH

ab +

b +a 2

6ab +a2 +b2

sin A =

2 ab

;

R =

a +b

6 +

+b2

a +b

2sin A

Ответ: r =

, R =

a +b

6 +

2 +b2

Задача 2.11. Доказать, что если диагонали вписанного четырехугольника взаимно перпендикулярны, то его несмежные

стороны стягивают дуги, сумма которых рана 180o .

Решение. Пусть четырехугольник				B
ABCD вписан в окружность, его диа-
				a

гонали AС и BD пересекаются в точке
					E
Е и AС BD (рис. 33).			A			C
Тогда CBD + ACB = 90o . Так
как углы CBD и ACB являются вписан-						m
ными, то

	1	1
				D
CBD = 2 CmD , ACB =		2 AaB .			Рис. 33

Следовательно,

12 CmD+ 12 AaB = 90o и CmD+ AaB =180o , что и требова-

лось доказать.

Вневписанная окружность и ее свойства

Вневписанной окружностью называется окружность,

касающаяся одной из сторон треугольника и продолжений двух других сторон. Центром вневписанной окружности является точка пересечения биссектрис двух внешних углов и биссектрисы внутреннего угла треугольника при третьей вершине.

Задача 2.12. Вычислить радиус вневписанной окружности, если известны площадь, полупериметр и сторона треугольника, которой касается эта окружность.

Решение. Пусть дан треугольник

ABC, где BC=a, AC=b и AB=c. Точка M

– центр вневписанной окружности, ка-

сающейся стороны a. Обозначим ради-

ус вневписанной окружности через ra

(рис.34). Чтобы вычислить радиус вне-

вписанной

окружности

рассмотрим

Рис. 34

площади

треугольников

ABC,

ABM,

ACM, BCM .

Имеем:

cra

bra

ara

SABC = SABM + SACM − SBCM

−

ra (b + c − a)

= r ( p − a),

где p – полупериметр треугольника ABC. Следовательно,

r =

p −a

Аналогично доказывается, что r

; r

p −b

p −c

где

и r - радиусы вневписанных окружностей,

касаю-

щихся сторон треугольника b и c соответственно.

Задача 2.13. Вневписанная

окружность

треугольника

АВС касается стороны ВС и продолжений сторон АВ и АС. Доказать, что отрезок от вершины А треугольника до точки касания вневписанной окружности, расположенной на продолжении стороны, равен полупериметру.

Решение. Пусть дан треугольник ABC, где BC=a, AC=b и AB=c, N и P – точки касания вневписанной окружности с продолжениями сторон AB и AC (рис. 34). Тогда

AN=AB+BN=c+BQ; AP=AC+CP=b+QC (BN=BQ, CP=QC, как отрезки касательных, проведенных из одной точки). Так как

AN=AP, то 2AN=b+c+BQ+QC=b+c+a=2p. Следовательно, AN=p.

Что и требовалось доказать.

Задача 2.14. Продолжение биссектрисы угла B треугольника ABC пересекают описанную окружность в точке M; O – центр вписанной окружности, Ib - центр вневписанной окруж-

ности, касающейся стороны AC. Доказать, что точки A, C, O и Ib лежат на окружности с центром в точке M (рис. 35).

Решение. Точка М является центром окружности, описанной около треугольника АОС (задача 2.6).Докажем, что

точка Ib лежит на этой
окружности.	Так	как
(1)	OAIb	прямо-
треугольник
угольный (AO и		A Ib	-	Рис. 35
биссектрисы	смежных		углов) и	AOM = MAO =ϕ , то

MAIb = MIb A = 90°−ϕ , а значит, MA = MIb . Таким образом, MIb = MA= MO =MC, что и требовалось доказать.

Задачи для самостоятельного решения

1.Определить площадь треугольника, если две его стороны равны 1 и 13 , а медиана третей стороны равна 2. (Ответ: 3 ).

2.Основание равнобедренного треугольника равно 32 , а медиана боковой стороны – 5.Найти длины боковых сторон треугольника. (Ответ: 6).

3.В равнобедренном треугольнике длина боковой стороны равна 4 10 , а длина медианы, проведенной к боковой стороне,

равна 6 3 . Найти длину основания треугольника. (Ответ: 10).

4. Две стороны треугольника равны соответственно 6 см и 8 см. Медианы, проведенные к этим сторонам, перпендикулярны.

Найти площадь треугольника (Ответ : 4 11 см2).

5.Медианы треугольника равны 3 см, 4 см и 5 см. Найти площадь треугольника. (Ответ:8 см2).

6.Две медианы треугольника взаимно перпендикулярны и

равны соответственно 3 см и 4 см. Найти площадь треугольника. (Ответ:8 см2).

7.Треугольник АВС, стороны которого 13 см, 14 см и 15 см, разбит на три треугольника отрезками, соединяющими точку М

пересечения медиан треугольника с вершинами треугольника. Найти площадь треугольника ВМС. (Ответ:28 см2).

8.Доказать, что если одна из медиан треугольника в полтора раза больше стороны, к которой она проведена, то две другие медианы треугольника взаимно перпендикулярны.

9.Найти боковые стороны равнобедренного треугольника, если тангенс угла при основании треугольника равен 3 и длина

медианы, проведенной к боковой стороне равна 6. (Ответ: 4 5 ).

10. Площадь тупоугольного треугольника АВС равна 9 7 ,

его медианы АК и СМ пересекаются под углом α = arccos 34 ,

АК : СМ=3:2. Найти стороны треугольника АВС. (Ответ АС=4,

АВ=2 58 , ВС= 2 43 ).

11. Площадь остроугольного треугольника АВС равна 24 2 ,

его медианы АК и СМ пересекаются под углом α = arccos 13 , АК

+ СМ=15. Найти стороны треугольника АВС. (Ответ:

АС=ВС=2 17 , АВ=8 2 , или ВС=8 2 , АС=АВ=2 17 ).

12. В треугольнике ABC сторона AC равна b , сторона AB равна c , а биссектриса внутреннего угла A пересекается со стороной BC в точке D такой, что DA = DB . Найти длину стороны

BC . (Ответ: b(b + c)).

13.Определить площадь треугольника, если две его стороны

равны 35 см и 14 см, а биссектриса угла между ними содержит

12 см. (Ответ: 235,2 см2).

14.Дан треугольник ABC , в котором угол B равен 30o , AB = 4 , BC = 6 . Биссектриса угла B пересекает сторону AC в

точке D . Определить площадь треугольника ABD . (Ответ: 2,4).

15. В треугольнике ABC проведена биссектриса BE , которую центр O вписанной окружности делит в отношении BO : OE = 2 . Найти AB , если AC = 7 , BC = 8 . (Ответ: 6).

<<< < Предыдущая 12 / 32 3 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
11.12.2019158.72 Кб0metrologia_voprosy_zachet2.doc
#
24.12.2019188.33 Кб0Mikrobiologia_otvety.docx
#
13.12.201932.47 Кб0MINISTERSTVO_OBRAZOVANIYa_I_NAUKI_ROSSII.docx
#
14.04.2019145.09 Кб30MMPI.docx
#
16.09.2019364.54 Кб4MODEL.DOC
#
31.05.2015438.45 Кб49mopg[1].pdf
#
30.05.201556.82 Кб66Moy_referat Готовый.docx
#
31.05.2015167.35 Кб17N 1-ФКЗ о военных судах.rtf
#
20.09.2019534.79 Кб57Nauki_o_Zemle.docx
#
22.12.2019676.86 Кб0Nina_Yakubenko_Olegovna_-_Shpargalka_po_informa...doc
#
27.11.201927.27 Кб4Non verbal Communication.docx