Mathematica / Глава 4. Евклидовы и факториальные кольца

2.2. По аналогии с gcd(a, b) вводится двойственное понятие наименьшего общего кратного m = lcm(a, b)

элементов a, b R, также определённого с точностью до ассоциированности двумя свойствами:

i') a|m, b|m.

ii') a|c, b|c m|c.

В частности, полагая с = ab, получаем m|ab.

Теорема 2.3. Пусть для элементов a, b целостного кольца R существуют gcd(a, b) и lcm(a, b).

Тогда:

а) gcd(a, b) = 0 a = 0 или b = 0.

б) a, b ≠ 0, m = lcm(a, b), ab = dm d = gcd(a, b).

2.4. Элементы a, b целостного кольца, в котором существует gcd, называются взаимно простыми, если gcd(a, b) = 1.

Из свойств i), ii), i'), ii') или из теоремы 2.3 нельзя извлечь ни способа вычисления, ни доказательства существования gcd(a, b) и lcm(a, b).

Пример 2.5. Наибольший общий делитель существует не всегда. Рассмотрим кольцо Z[ 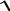−5 ] всех целых чисел с добавленным элементом −5 . Число 2 делит 6 и 2 + 2 −5 . Точно также 1 + −5 является делителем и 2 + 2 −5 и 6, так как 6 = (1 + −5 ) (1 – −5 ). Но здесь нет кратного двух элементов 2 и 1 + −5 , которое бы было делителем и 6 и 2 + 2 −5 .

Но для евклидовых колец наибольший общий делитель существует и вычисляется просто.

Теорема 2.6. В евклидовом кольце R любые два элемента a, b имеют наибольший общий делитель и наименьшее общее кратное. Более того, существует алгоритм, с помощью которого можно найти gcd(a, b) и такие u, v R, что выполнено соотношение Безу:

gcd(a, b) = au + bv.

Замечание. Пара элементов х, y в соотношении Безу ax + by = gcd(a, b).

не единственная. На самом деле таких пар бесконечно много.

Например, если мы возьмем u, v, для которых выполнено (4), и произвольное целое k, то, как несложно проверить,

a(u + kb) + b(v – ka) = gcd(a, b).

Утверждение теоремы 2.6 легко распространяются на случай произвольного конечного числа элементов евклидова кольца.

Следствие 2.7. Пусть a, b, c – элементы евклидова кольца R.

i)Если gcd(a, b) = 1 и gcd(a, c) = 1, то gcd(a, bc) = 1.

ii)Если a|bc и gcd(a, b) = 1, то a|c.

iii)Если b|a, c|a и gcd(b, c) = 1, то bc|a.

Следствие 2.8. Если R – одно из колец Z, Z[i] или P[x], где P – поле, то для любых двух элементов a, b R (одновременно ненулевых) существует gcd(a, b), для которого выполняется соотношение Безу, и наибольший общий делитель можно найти с помощью алгоритма Евклида.

Рассмотрим свойства gcd в различных кольцах. Начнем с Z.

Для вычисления gcd(m, n) заданных целых чисел

0 ≤ m < n можно в алгоритме Евклида использовать рекурсию

gcd (0, n) = n,

gcd(m, n) = gcd(n mod m, m) при m>0.

Указанная рекурсия законна потому, что любой общий делитель чисел m и n должен быть также общим делителем чисел m и n mod m.

Количество операций mod в алгоритме оценивается сверху величиной 5 log10m.

Текст программы алгоритма Евклида на языке Wolfram gcd(m, n):

gcd[m_, n_] := If[m == 0, n, gcd[Mod[n, m], m]]

Алгоритм 2.9. Расширенный рекурсивный алгоритм Евклида (A Extended Euclidean Algorithm) вычисляет для целых m, n тройку чисел x, y, d, удовлетворяющих соотношению Безу

x m + y n = d =gcd(m, n).

Вход алгоритма: m, n. Выход: {x, y, d} = EEA(m, n): If m = 0 then return({0, 1, n})

else begin

r = n mod m;

{r1, m1, d} = EEA(r, m); (* рекурсивный вызов *)

return({m1 – n/m r1, r1, d}) end

Текст программы в системе Mathematica:

eea[m_, n_] := Module[{d, r1, m1}, If[m == 0, {0, 1, n}, r = Mod[n, m];

{r1, m1, d} = eea[r, m];

{m1 – Quotient[n, m] r1, r1, d}]]

Функция GCD[n1, n2, …, nk] в Mathematica вычисляет наибольший общий делитель n1, n2, …, nk.

Аргументы могут быть и рациональными числами.

GCD[100!, 500!, 1000!, 10000!] == 100!

True

Функция ExtendedGCD[n1, n2, …, nk] вычисляет расширенный наибольший общий делитель n1, n2, …, nk.

{g, {a, b, c}} = ExtendedGCD[6, 15, 30]

{3, {–2, 1, 0}}

6a + 15b + 30c == g

True

Нахождение gcd в кольце Q[x]

Если f и g – многочлены относительно одной общей переменной и с коэффициентами из Q, то

PolynomialGCD[f, g] вычисляет gcd(f, g).

PolynomialGCD[3(1+x)^2(2+x)(4+x),

2(1+x)(2+x)(3+x)]

(1 + x)(2 + x)

Если коэффициенты многочленов целые, то результатом является нормированный многочлен, то есть старший коэффициент gcd равен 1.

Все символьные параметры в многочленах трактуются функцией PolynomialGCD как переменные, поэтому при наличии нескольких переменных эта функция вычисляет наибольший общий делитель для многочленов от нескольких переменных.

Функция находит gcd и в случае более двух многочленов:

PolynomialGCD[x^2-1, x^3-1, x^4-1, x^5-1, x^6-1, x^7- 1]

– 1 + x

Вычислительные трудности алгоритма Евклида

При нахождении gcd многочленов над полем Q с помощью алгоритма Евклида часто происходит значительное увеличение размеров рациональных чисел в промежуточных вычислениях, если даже результат содержит небольшие числа.

Пример 2.10.

u = x^8 + 5 x^7 + 7 x^6 – 3 x^5 + 4 x^4 + 17 x^3 – 2 x^2 – 6 x + 3;

v = x^8 + 6 x^7 + 3 x^6 + x^5 + 10 x^4 + 8 x^3 + 2 x^2 + 9 x + 8;

Получаем последовательность остатков: r1 = PolynomialRemainder[u, v, x]

-5 -15 x -4 x2 +9 x3 -6 x4 -4 x5 +4 x6 -x7

r2 = PolynomialRemainder[v, r1, x]

-42 -146 x -53 x2 +94 x3 -41 x4 -45 x5 +39 x6

r3 = PolynomialRemainder[r1, r2, x]