Госы 5к Надя / уравнения математической физики / Модуль 2 / лекции / 9

Колебания мембраны Лекция №9

Тема: Колебания мембраны.

Вопросы:

1. Задача об осесимметричных колебаниях круглой мембраны.

2. Решение задачи о колебаниях мембраны методом Фурье. Уравнение и функции Бесселя.

Мембраной будем называть свободно изгибающуюся натянутую пленку.

Пусть в положении равновесия мембрана совпадает с некоторой ограниченной областью плоскости хОу с кусочно-гладкой границей Г. Тогда функция , определяющая эти колебания, должна удовлетворять уравнению

, (7.1)

начальным условиям

, (7.2)

при . Здесь первое условие определяет начальное отклонение, а второе – начальную скорость. На границе же области функция должна удовлетворять каким-нибудь граничным условиям. В простейшем случае полагаем

, при . (7.3)

Применяя метод разделения переменных, положим

.

Аналогично одномерному случаю, получим следующие уравнения для функций и (проверить самостоятельно!):

, (7.4)

. (7.5)

Рассмотрим частный случай – колебания круглой мембраны. Пусть круглая мембрана радиуса с центом в начале координат, закреплена по окружности круга. Введем на плоскости полярные координаты и произведем замену переменных по формулам

, , .

Таким образом,

, , .

Тогда

,

.

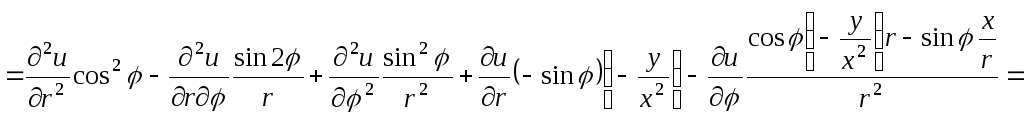
Аналогично,

.

Таким образом,

и уравнение свободных колебаний мембраны в полярных координатах примет вид

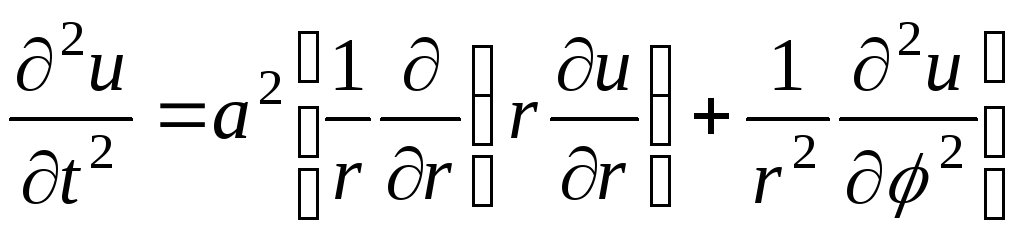. (7.6)

Начальные и граничные условия примут вид

, (7.7)

,

. (7.8)

Ограничимся важным частным случаем, осесимметричных колебаний, когда начальные функции и не зависят от . Таким образом, все точки окружности радиуса с центром в начале координат в начальный момент времени имеют скорости и отклонения, не зависящие от угла . Тогда уравнение (7.6) упрощается:

, (7.9)

при граничном условии

(7.10)

и начальных условиях

, (7.11)

.

Решения уравнения (7.9) будем искать методом Фурье в виде

,

тогда

,

или

.

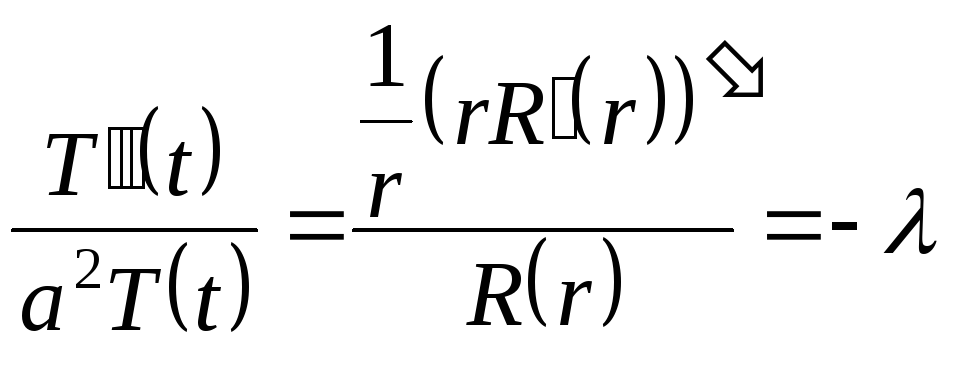Отсюда получаем уравнения

, (7.12)

, (7.13)

, . (7.14)

Условие выражает требование ограниченности решения в центре мембраны, т.е. при . Задача (7.13), (7.14) имеет очевидное тривиальное решение, которое нас не устраивает. Таким образом, нам нужно найти собственные значения параметра , при которых задача имеет нетривиальные решения.

Уравнение (7.12) имеет решение

,

где - положительная постоянная.

Приведем уравнение (7.13) к стандартному виду, введя новую независимую переменную и положив

.

Тогда

,

и, следовательно, для функции мы получаем уравнение

,

или

. (7.15)

Уравнение (7.15) является уравнением Бесселя.

Решение уравнения (7.15) будем искать в виде

.

С учетом того, что

,

из (7.15) получаем

,

или

.

Сравнивая коэффициенты при одинаковых степенях х получим, что

, , (7.16)

,

Из первых двух равенств (7.16) следует, что

, ,

а из третьего

,

Все коэффициенты , а

.

Следовательно,

,

таким образом,

.

При решение уравнения Бесселя обозначается через и называется функцией Бесселя нулевого порядка. Более подробно о функциях Бесселя можно прочитать в книге В.С. Владимирова «Уравнения математической физики».

Таким образом,

.

Поэтому

Используя граничные условия, получим

,

следовательно, число должно быть одним из нулей функции Бесселя, т.е.

,

где - нуль функции . Известно, что функция имеет бесконечное множество положительных нулей

,

откуда получаем собственные значения

, ,

и собственные функции

_,

задачи (7.13), (7.14).

При общее решение уравнения (7.12) имеет вид

.

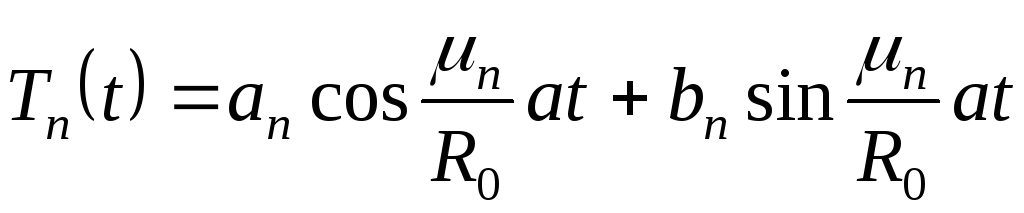Функция

будет решением уравнения (7.9), удовлетворяющим граничному условию (7.10).

Решение исходной задачи будет иметь вид

,

если конечно числа достаточно быстро стремятся к нулю, чтобы ряды можно было дважды почленно дифференцировать. Коэффициенты определим из начальных условий

, (7.17)

.

Функции Бесселя обладают свойствами, сходными со свойствами тригонометрических функций. Если функция кусочно-гладкая на , то она разлагается в ряд (7.17).

Тригонометрические функции ортогональны на , функции Бесселя также ортогональны на , но с весом r:

_{, .}

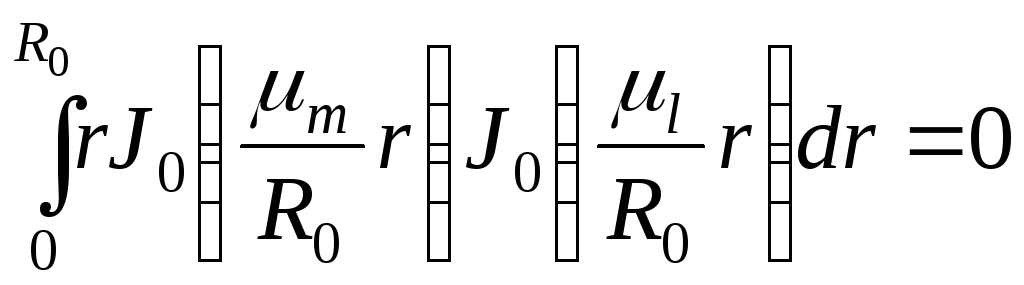Умножим ряд (7.17) на и, так как его равномерная сходимость от этого не нарушается, проинтегрируем почленно по , тогда

, ,

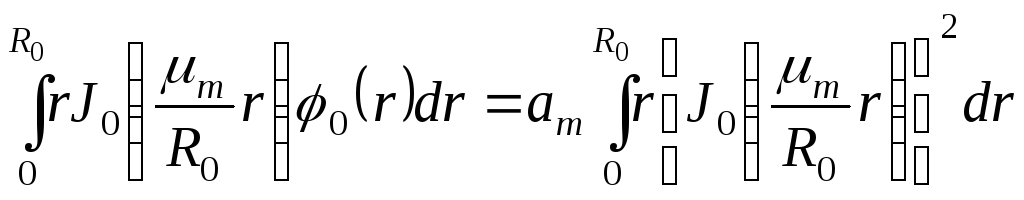следовательно,

.

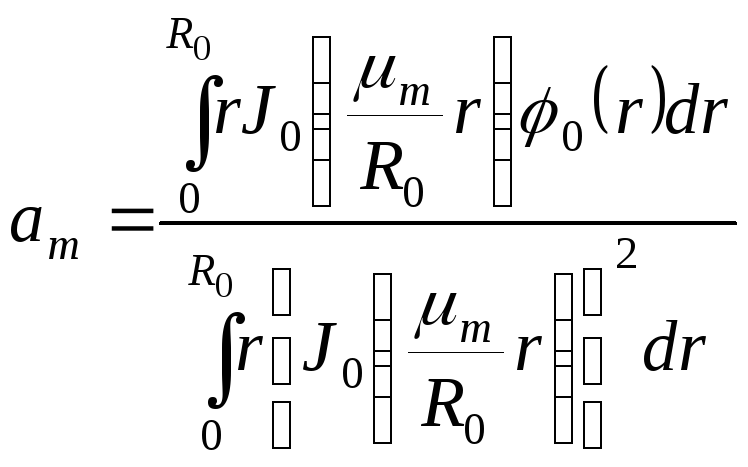Аналогично,

.

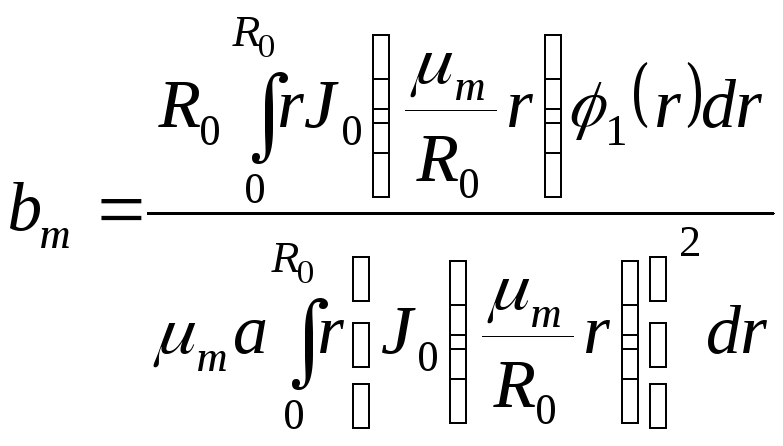46