
- •1. Дифференциальные уравнения в частных производных
- •1.1 Определение дифференциальных уравнений в частных производных параболического типа
- •1.2 Приведение уравнения второго порядка параболического типа к каноническому виду
- •1.3 Постановки задач для уравнений параболического типа
- •2. Численное решение дифференциальных уравнений
- •2.1 Основные определения и конечно-разностные схемы для дифференциальных уравнений параболического типа
- •2.1.1 Основные определения. Принцип построения разностных схем
- •2.1.2 Аппроксимация и сходимость разностных схем
- •2.1.3 Исследование устойчивости конечно-разностных схем
- •2.2 Конечно-разностный метод решения задач для уравнений параболического типа
- •2.2.1 Однородные и консервативные конечно-разностные схемы для задач теплопроводности с граничными условиями, содержащими производные
- •2.2.2 Неявно-явная конечно-разностная схема с весами. Схема Кранка-Николсона
- •2.2.3 Метод дробных шагов н.Н. Яненко
- •2.2.4 Метод переменных направлений с экстраполяцией в. Ф. Формалева
- •2.3 Численное решение определенных задач
1.3 Постановки задач для уравнений параболического типа
Классическим примером уравнения параболического типа является уравнение теплопроводности (диффузии). В однородной среде (без источников энергии) уравнение теплопроводности или диффузии имеет вид
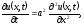
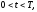 (1.17)
(1.17)
где
u – температура,
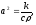 k
– коэффициент теплопроводности, c –
удельная теплоемкость,
k
– коэффициент теплопроводности, c –
удельная теплоемкость,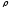 - плотность (в задаче диффузии u –
концентрация диффундирующего вещества,
- плотность (в задаче диффузии u –
концентрация диффундирующего вещества,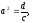 d - коэффициент диффузии, c – коэффициент
пористости среды, который определяется
отношением объема пор к рассматриваемому
объему), x=0 и x=L левый и правый концы
отрезка изменения пространственной
переменной, t=0 и t=T – моменты начала и
окончания процесса. На множестве
d - коэффициент диффузии, c – коэффициент
пористости среды, который определяется
отношением объема пор к рассматриваемому
объему), x=0 и x=L левый и правый концы
отрезка изменения пространственной
переменной, t=0 и t=T – моменты начала и
окончания процесса. На множестве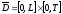 рассматриваются различные начально-краевые
задачи для уравнения (4) (рис. 1.1)
рассматриваются различные начально-краевые
задачи для уравнения (4) (рис. 1.1)
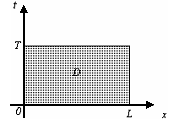
Рис. 1.1 - Область D ограниченная прямоугольником
Первая начально-краевая задача:
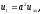
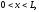
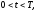 (1.18)
(1.18)

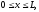 (начальное
условие)
(начальное
условие)
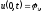
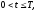 (краевое
условие на левой границе)
(краевое
условие на левой границе)
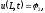
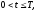 (краевое
условие на правой границе)
(краевое
условие на правой границе)
содержит
функциональное начальное условие (при
t=0) и функциональные краевые условия на
левой (x=0) и правой (x=L) границах области.
Где
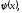
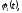
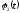 –
заданные функции.
–
заданные функции.
Вторая начально-краевая задача:
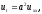
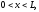
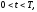 (1.19)
(1.19)
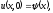
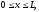 (начальное
условие)
(начальное
условие)
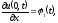
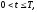 (краевое
условие на левой границе)
(краевое
условие на левой границе)
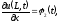
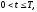 (краевое
условие на правой границе)
(краевое
условие на правой границе)
содержит функциональное начальное условие (при t=0) и дифференциальные краевые условия на левой (x=0) и правой (x=L) границах области.
Третья начально-краевая задача:
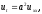
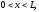
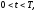 (1.20)
(1.20)
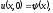
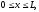 (начальное
условие)
(начальное
условие)
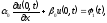
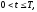 (краевое
условие на левой границе)
(краевое
условие на левой границе)
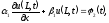
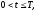 (краевое
условие на правой границе)
(краевое
условие на правой границе)
содержит
функциональное начальное условие (при
t=0) и функционально-дифференциальные
краевые условия на левой (x=0) и правой
(x=L) границах области. Где
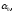
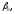
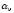
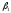 –
заданные числа
–
заданные числа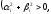
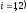 .
.
Задача Коши:
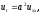
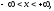
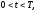
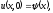
 (начальное
условие)
(начальное
условие)
содержит только функциональное начальное условие (при t=0) и рассматривается в бесконечной области изменения пространственной переменной.
Примером
физической задачи, приводящей к первой
начально-краевой задаче служит процесс
теплопередачи по длинному тонкому
стержню, лежащему вдоль оси Ox от x=0 до
x=L (ось стержня совпадает с осью Ox).
Предполагается, что в точке x=0 температура
изменяется со временем по закону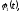 а
в точке x=L по закону
а
в точке x=L по закону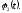 В начальный момент времени при t=0 функцией
В начальный момент времени при t=0 функцией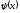 задано начальное распределение
температуры вдоль стержня. Тогда
распределение температуры вдоль него
во все последующие моменты времени
определяется решением начально-краевой
задачи с уравнением (1.7), где
задано начальное распределение
температуры вдоль стержня. Тогда
распределение температуры вдоль него
во все последующие моменты времени
определяется решением начально-краевой
задачи с уравнением (1.7), где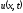 –
температура стержня в некоторой точке
x в момент времени t.
–
температура стержня в некоторой точке
x в момент времени t.
Во
всех перечисленных задачах требуется
найти функцию
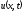 ,
которая удовлетворяет дифференциальному
уравнению (1.7) в области D и соответствующим
условиям на ее границе.
,
которая удовлетворяет дифференциальному
уравнению (1.7) в области D и соответствующим
условиям на ее границе.
2. Численное решение дифференциальных уравнений
2.1 Основные определения и конечно-разностные схемы для дифференциальных уравнений параболического типа
2.1.1 Основные определения. Принцип построения разностных схем
Точное решение задач математической физики (в виде явных формул, рядов и т.п.) можно найти только в редких случаях. Среди приближенных методов, наиболее применимы разностные методы (методы сеток). Сущность разностных методов состоит в том, что исходная область изменения независимых переменных заменяется дискретным множеством точек – сеток, а производные, входящие в уравнение, аппроксимируются на этой сетке разностными соотношениями. В результате исходная линейная задача заменяется системой конечного числа линейных алгебраических уравнений, называемой разностной схемой (задачей), а исходная нелинейная задача заменяется нелинейной разностной схемой. За приближенное решение исходной задачи принимается решение разностной схемы. Точность приближения зависит от способа аппроксимации и от густоты сетки.
Пусть дана исходная (дифференциальная) задача в виде
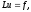 (2.1)
(2.1)
где
u – искомая функция, определенная на
множестве
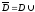 Г;
D – область пространства независимых
переменных с границей Г; f – заданная
функция, L – линейный дифференциальный
оператор. Все производные, входящие в
дифференциальной уравнение, перенесены
в левую часть, а остальные функции
образуют правую часть; дополнительные
условия (начальные и краевые) также
включены, а оператор и правую часть f.
Г;
D – область пространства независимых
переменных с границей Г; f – заданная
функция, L – линейный дифференциальный
оператор. Все производные, входящие в
дифференциальной уравнение, перенесены
в левую часть, а остальные функции
образуют правую часть; дополнительные
условия (начальные и краевые) также
включены, а оператор и правую часть f.
Для
численного решения задачи вводится
сетка
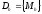 – конечное множество точек Mh (узлов
сетки), принадлежащих
– конечное множество точек Mh (узлов
сетки), принадлежащих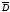 ,
плотность размещения которых
характеризуется параметром h - шагом
сетки. В общем случае h – вектор,
компонентами которого являются шаги
по всем независимым переменным решаемой
задачи, с длиной
,
плотность размещения которых
характеризуется параметром h - шагом
сетки. В общем случае h – вектор,
компонентами которого являются шаги
по всем независимым переменным решаемой
задачи, с длиной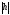 .
Обычно сетка задается так, что при
.
Обычно сетка задается так, что при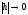 множество Dh стремится заполнить множество
множество Dh стремится заполнить множество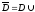 Г.
Г.
Рассмотрим некоторую дифференциальную задачу с двумя независимыми переменными x и t. Для простоты изложения множество D представляет собой прямоугольник длины l и высоты T, ограниченный отрезками прямых, параллельных осям Ox и Ot (рис. 2.1), т. е. задана двумерная прямоугольная сетка
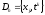 ,
,
где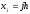 ,
,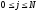 ;
;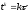 ,
N, K – целые положительные числа; h,
,
N, K – целые положительные числа; h, -
величины шагов по пространству и времени
(для простоты принимаются постоянными);
-
величины шагов по пространству и времени
(для простоты принимаются постоянными);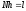 ,
, .
Такая сетка называется равномерной
(регулярной). В данном случае
.
Такая сетка называется равномерной
(регулярной). В данном случае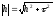 или
или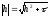 .
Узлы, принадлежащие промежуткам
.
Узлы, принадлежащие промежуткам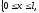
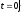 ,
,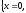
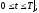
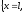

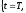
 ,
называются граничными, а остальные –
внутренними. Слоем
,
называются граничными, а остальные –
внутренними. Слоем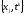 ,
,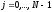 ;
;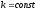 называется множество всех узлов сетки,
имеющих одну и ту же временную координату
называется множество всех узлов сетки,
имеющих одну и ту же временную координату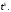

Рис. 2.1 - Конечно-разностная сетка
Функции,
определенные в точках сетки
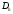 ,
называются сеточными. Введем сеточную
функцию
,
называются сеточными. Введем сеточную
функцию

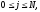
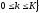 ,
(2.2)
,
(2.2)
с
пространственным шагом
 и шагом по времени
и шагом по времени (рис. 2.1). Данная функция является сеточным
представлением решения исходной
(дифференциальной) задачи или точным
решением дифференциальной задачи в
узлах сетки. Вычислить
(рис. 2.1). Данная функция является сеточным
представлением решения исходной
(дифференциальной) задачи или точным
решением дифференциальной задачи в
узлах сетки. Вычислить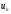 не удается, поэтому находят другую
сеточную функцию
не удается, поэтому находят другую
сеточную функцию ,
приближенно совпадающую с точным
решением в узлах сетки. Она вычисляется
как решение разностной схемы
,
приближенно совпадающую с точным
решением в узлах сетки. Она вычисляется
как решение разностной схемы
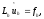 (2.3)
(2.3)
в
некотором смысле соответствующей задаче
(2.1). Здесь Lh – разностный оператор,
аппроксимирующий линейный дифференциальный
оператор B (он формируется в результате
аппроксимации частных производных,
входящих в B, соответствующими
конечно-разностными соотношениями);
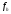 - сеточная функция, возникающая в
результате замены правой части уравнения
(2.1) значениями в узлах сетки. Под
разностной схемой понимается совокупность
разностных уравнений, аппроксимирующих
основное дифференциальное уравнение
во всех внутренних узлах сетки и
дополнительные условия (начальные и
краевые) – в граничных узлах. Разностную
схему будем называть разностной задачей
по аналогии с дифференциальной задачей.
- сеточная функция, возникающая в
результате замены правой части уравнения
(2.1) значениями в узлах сетки. Под
разностной схемой понимается совокупность
разностных уравнений, аппроксимирующих
основное дифференциальное уравнение
во всех внутренних узлах сетки и
дополнительные условия (начальные и
краевые) – в граничных узлах. Разностную
схему будем называть разностной задачей
по аналогии с дифференциальной задачей.
Введем
на конечно-разностной сетке (2.2) два
временных слоя: нижний
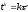 ,
на котором распределение искомой функции
,
на котором распределение искомой функции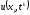 ,
, ,
и верхний временной слой
,
и верхний временной слой ,
на котором распределение искомой функции
,
на котором распределение искомой функции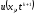 ,
,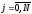 подлежит определению.
подлежит определению.
На
введенной сетке (2.2) введем сеточные
функции
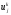 ,
,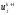 ,
первая из которых известна, вторая –
подлежит определению. Для ее определения
в задаче (1.18) заменим (аппроксимируем)
дифференциальные операторы отношением
конечных разностей, получим
,
первая из которых известна, вторая –
подлежит определению. Для ее определения
в задаче (1.18) заменим (аппроксимируем)
дифференциальные операторы отношением
конечных разностей, получим
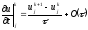 ,
(2.4)
,
(2.4)
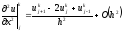 (2.5)
(2.5)
Подставляя (2.4), (2.5) в задачу (1.18), получим явную конечно-разностную схему для этой задачи в форме
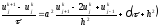 ,
,
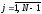 ,
,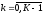 ;
;
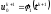 ,
,
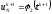 ,
,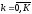 (2.6)
(2.6)
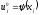 ,
,
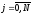 .
.
В
каждом уравнении этой задачи все значения
сеточной функции известны, за исключением
одного,
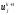 ,
которое может быть определено явно из
соотношений (2.6). В соотношения (2.6) краевые
условия входят при значениях j=1 и j=N–1,
а начальное условие – при k=0.
,
которое может быть определено явно из
соотношений (2.6). В соотношения (2.6) краевые
условия входят при значениях j=1 и j=N–1,
а начальное условие – при k=0.
Определение
1. Схема называется явной, если оператор
L аппроксимируется с использованием
известных значений функции
 на n-м слое, а аппроксимирующее уравнение
содержит только одно неизвестное
значение функции на следующем
на n-м слое, а аппроксимирующее уравнение
содержит только одно неизвестное
значение функции на следующем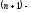 м
слое, которое нетрудно выразить явно.
м
слое, которое нетрудно выразить явно.
Если в (2.5) дифференциальный оператор по пространственной переменной аппроксимировать отношением конечных разностей на верхнем временном слое:
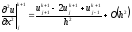
 (2.7)
(2.7)
то после подстановки (2.4), (2.7) в задачу (1.18), получим неявную конечно-разностную схему для этой задачи:
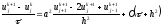 ,
,
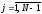 ,
,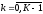 ;
;
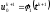 ,
,
 ,
,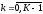 (2.8)
(2.8)
 ,
,
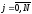 .
.
Теперь
сеточную функцию
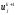 на верхнем временном слое можно получить
из решения СЛАУ (2.8) с трехдиагональной
матрицей.
на верхнем временном слое можно получить
из решения СЛАУ (2.8) с трехдиагональной
матрицей.
Определение
2. Схема называется неявной, если оператор
аппроксимируется с использованием
нескольких неизвестных значений искомой
функции на
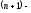 м
слое.
м
слое.
Узлы
сетки
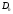 ,
значения в которых используется при
аппроксимации оператора B, образуют
шаблон.
,
значения в которых используется при
аппроксимации оператора B, образуют
шаблон.
Шаблоном конечно-разностной схемы называют ее геометрическую интерпритацию на конечно-разностной сетке.
При
изображении шаблона светлыми кружочками
обозначаются узлы на k-м слое с известными
значениями функции, а зачеркнутыми –
узлы на
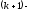 м
слое с неизвестными значениями функции,
подлежащие определению. Шаблон, содержащий
p узлов, называется p-точечным.
м
слое с неизвестными значениями функции,
подлежащие определению. Шаблон, содержащий
p узлов, называется p-точечным.
На рис. 2.2 приведены шаблоны для явной (2.6) и неявной (2.8) конечно-разностных схем при аппроксимации задачи (1.18).
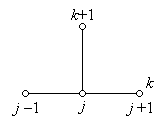
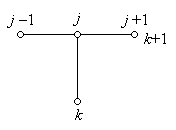
а б
Рис. 2.2 - Шаблоны явной (а) и неявной (б) конечно-разностных схем для уравнения теплопроводности
