5. Разложение определителя по ряду. Минор и алгебраическое дополнение к элементу определителя. Связь алгебраических дополнений с минорами.

Пусть Δ = =.

Определение 1. Если в определителе Δ сгруппировать все слагаемые, содержащие элемент a_ij и, сгруппировав, вынести элемент a_ij за скобки, то выражение, полученное в скобках, обозначается A_ij и называется алгебраическим дополнением к элементу a_ij в определителе Δ, i = ,j = .

Так как все элементы i-той строки определителя Δ входят в одно и только одно из слагаемых, то Δ=a_i1A_i1+ a_i2A_{i2+ … +} a_inA_in (1). Равенство (1) называется разложением определителя Δ по i-той строке.

Аналогично: Δ=a_1jA_1j+ a_2jA_{2j+ … +} a_njA_nj (2) - разложение определителя Δ по j-тому столбцу, j =.

Строки и столбцы определителя Δ называются его рядами. Таким образом, (1) и (2) – разложения Δ по ряду.

Определение 2. Если в определителе Δ вычеркнуть i-тую строку и j-тый столбец, то на их пересечении получится элемент a_ij, а остальные элементы образуют определитель (n-1)-го порядка, который обозначается M_ij и называется минором к элементу a_ij в определителе Δ, i = ,j = .

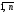Пример 1. Пусть Δ = . ТогдаM₂₃ =и т.д.

Теорема 1. Пусть Δ - определитель n-го порядка над полем P, A_ij и M_ij – алгебраическое дополнение и минор к элементу a_ij в Δ соответственно. Тогда

A_ij=(-1)^{i+ j}M_ij, i = ,j = .

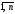Доказательство. Пусть Δ₁ - сумма всех тех слагаемых из Δ, которые содержат элемент a_ij, т.е. Δ₁==(3). Вторые индексы в (3) образуют перестановкуI₁, полученную из перестановки I удалением символа j с i-того места. Тогда, по теореме о четности перестановки, получим ==a_ij(-1)^i+jM_ij, т.е. Δ₁ = a_ij(-1)^i+jM_ij (4). С другой стороны Δ₁ =a_ijA_ij (5). Из (4) и (5) следует, что a_ij(-1)^i+jM_ij = a_ijA_ij. Тогда A_ij = (-1)^i+jM_ij. Теорема доказана.

6. Свойства определителей.

Свойство 1. При транспонировании матрицы ее определитель не изменяется.

Доказательство. Пусть - матрицаn-го порядка над полем Р. Транспонируя А, получим . Всевозможные произведения видабудут одинаковыми как для матрицы А, так и для матрицы^tА. При этом знак произведения сохраняется. Таким образом, ∣А∣=∣ ^tА∣.

Из свойства 1 следует, что все утверждения, справедливые для какой-либо строки определителя, верны и для его столбца

Свойство 2. Если все элементы некоторой строки определителя равны нулю, то определитель равен нулю.

Доказательство. В каждое произведение определителя обязательно входит один элемент строки, состоящей из нулей. Поэтому все слагаемые определителя раны нулю, а, значит, и определитель равен нулю.

Свойство 3. От перестановки двух строк местами определитель меняет знак.

Доказательство. Пусть Δ = .

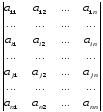В определителе Δ переставим i-ю и j-ю (i<j) строки местами. Получим:

Δ '= . Пусть- одно из произведений определителя Δ. Тогда соответствующим для определителя Δ' будет произведение. Эти произведения различаются только индексами сомножителей. Перестановка (k₁ k₂ … k_j … k_i … k_n) получена из перестановки (k₁ k₂ … k_i … k_j … k_n). Такое преобразование меняет четность перестановки, а, следовательно, знак рассматриваемого произведения. Таким образом, при перестановке двух строк местами все произведения, составляющие определитель Δ, поменяют знак. Следовательно, поменяет знак и Δ.

Свойство 4. Определитель, содержащий две одинаковые строки, равен нулю.

Доказательство. Пусть определитель Δ содержит две одинаковые строки: i-ю и j-ю. Поменяем их местами. По свойству 3, определитель Δ поменяет знак: Δ'=-Δ. Но, так как строки одинаковые, то Δ'=Δ. Значит, Δ=-Δ и Δ=0. Свойство доказано.

Свойство 5. Общий множитель всех элементов некоторой строки определителя можно вынести за знак определителя.

Доказательство. Δ = =. Пусть элементыi-ой строки имеют общий множитель α. Так как в каждое слагаемое вида входит элемент этой строки, то все такие произведения имеют общий множительα, который можно вынести за знак всей суммы в Δ.

Свойство 5'. Если все элементы некоторой строки определителя Δ умножить на одно и тоже число, то определитель умножится на это число.

Свойство 6. Определитель, содержащий две пропорциональные строки, равен нулю.

Доказательство. Пусть Δ = , причемa_i1=a_j1, a_i2=a_j2, …, a_in=a_jn. Вынесем элемент α из j-ой строки за знак определителя Δ. Получим:

Δ = . Тогда, по свойству 4, Δ =α⋅0=0.

Свойство 7. Если все элементы i-ой строки определителя представлены в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки, кроме i-ой, те же, что и у данного определителя, i-я строка одного определителя состоит из первых слагаемых i-ой строки данного определителя, а i-я строка второго – из вторых слагаемых i-ой строки данного определителя.

Свойство 8. Определитель не изменится, если к элементам одной строки прибавить соответствующие элементы другой строки, умноженные на одно и то же число.

Свойство 9. Сумма произведений элементов какой-либо строки определителя n-го порядка на алгебраические дополнения соответствующих элементов другой строки равна нулю, то есть a_i1A_j1+a_i2A_j2+…+a_inA_jn=0 где i≠j.

13