Примерная схема решения задач по кинематике колебаний

Решение задач этого раздела рекомендуется выполнять в следующем порядке:

• выбрать систему отсчета, взяв начало координат в положении равновесия материальной точки;

• записать начальные условия движения материальной точки;

• составить дифференциальное уравнение движения материальной точки в проекции на соответствующую ось;

• проинтегрировать дифференциальное уравнение движения, использовав начальные условия движения для определения постоянных интегрирования.

При составлении дифференциального уравнения движения надо изобразить материальную точку в промежуточном положении, соответствующем ее положительной координате, предположив при этом, что точка перемещается в сторону возрастания этой координаты.

Пример 1.3.

Материальная точка колеблется по закону . При значениях координаты Х₁ и Х₂ ее скорость равна V₁ и V₂. Определить амплитуду и период колебаний.

A=?, T=? Х1 ,V1 Х2, V2

Решение

Найдем скорость колеблющейся материальной точки. По определению скорости имеем:

.

Используя данные задачи, образуем систему уравнений:

Выражая из полученных уравнений функции синуса и косинуса для моментов времени t₁ и t₂ и воспользовавшись тригонометрической единицей , получим:

и .

Решая систему, имеем:

,

Задачи к главе I для самостоятельного решения

1. Две прямые дороги пересекаются под углом α = 60⁰. От перекрестка по ним удаляются машины: одна со скоростью V₁ = 60 км/ч, другая со скоростью V₂ = 80 км/ч. Определить скорости V' и V", с которыми одна машина удаляется от другой. Перекресток машины прошли одновременно.

V' = 122 κм/ч, V" = 72,2 км/ч.

2. Точка двигалась в течение t₁ = 15 с со скоростью V₁ = 5 м/с, в течение t₂ = 10 с со скоростью V₂ = 8 м/с и в течение t₃ = 6 с со скоростью V₃ = 20 м/с. Определить среднюю путевую скорость <V> точки.

<V> = 8,87 м/с.

1.3. Первую половину пути тело двигалось со скоростью V₁ = 2 м/с, вторую – со скоростью V₂ = 8 м/с. Определить среднюю путевую скорость <V>.

<V> = 2 V₁ V₂ /( V₁ + V₂ ) = 3,2 м/с.

1.4. Рядом с поездом на одной линии с передними буферами паровоза стоит человек. В тот момент, когда поезд начал двигаться с ускорением а = 0,1 м/с², человек начал идти в том же направлении со скоростью V = 1,5 м/с. Через какое время t поезд догонит человека? Определить скорость V₁ поезда в этот момент и путь, пройденный за это время человеком.

30 с; 3 м/с; 45 м.

1.5. Из одного и того же места начали равноускоренно двигаться в одном направлении две точки, причем вторая начала свое движение через 2 с после первой. Первая точка двигалась с начальной скоростью V₁ = 1 м/с и ускорением а₁ = 2 м/с², вторая – с начальной скоростью V₂ = 10 м/с и ускорением а₂ = 2 м/с². Через сколько времени и на каком расстоянии от исходного положения вторая точка догонит первую?

Встретятся дважды: через 3,4 с на расстоянии 15 м и через 10,6 с,

на расстоянии 123 м..

1. 6. С какой высоты Н упало тело, если последний метр пути оно прошло за время t = 0,1 с?

Н = (2s + gt²)²/ (8gt²) = 5,61 м, где s = 1 м.

1.7. Камень падает с высоты h = 1200 м. Какой путь s пройдет камень за последнюю секунду своего падения?

S=150 м.

1.8. Камень брошен вертикально вверх с начальной скоростью V₀ = 20 м/с. По истечении какого времени камень будет находиться на высоте h = 15 м? Найти скорость V камня на этой высоте. Сопротивлением воздуха пренебречь. Принять g = 10 м/с².

м/с (при движении вверх); 3 с; -10 м/с (при падении).)

1.9. Точка движется по кривой с постоянным тангенциальным ускорением а_τ = 0,5 м/с². Определить полное ускорение а точки на участке кривой с радиусом кривизны R = 3 м, если точка движется на этом участке со скоростью V = 2 м/с.

а=1,42 м/с².

1.10. Точка движется по окружности радиусом R = 4 м. Начальная скорость V₀ точки равна 3 м/с , тангенциальное ускорение а_τ = 1 м/с². Для момента времени t = 2 c определить: 1) длину пути s, пройденного точкой; 2) модуль перемещения ; 3) среднюю путевую скорость <V>; 4) модуль вектора средней скорости .

1) 8 м; 2) 6,73 м; 3) 4 м/с; 4) 3,36 м/с.

1.11. По дуге окружности радиусом R = 10 м движется точка. В некоторый момент времени нормальное ускорение точки а_n = 4,9 м/с²; в этот момент векторы полного и нормального ускорений образуют угол  = 60⁰. Найти скорость V и тангенциальное ускорение а_τ точки.

8,5 м/с².

1.12. Точка движется по окружности радиусом R = 2 м согласно уравнению = Аt³, где А = 2 м/с². В какой момент времени t нормальное ускорение а_n будет равно тангенциальному а_τ? Определить полное ускорение а в этот момент. В заданном уравнении движения ξ означает криволинейную координату, отсчитанную от некоторой начальной точки на окружности.

0,872 с; 14,8 м/с².

1.13. С вышки бросили камень в горизонтальном направлении. Через промежуток времени t = 2 c камень упал на землю на расстоянии s = 40 м от основания вышки. Определить начальную V₀ и конечную V скорости камня.

20 м/с; 28 м/с.

1.14. Пистолетная пуля пробила два вертикально закрепленных листа бумаги, расстояние L между которыми равно 30 м. Пробоина во втором листе оказалась на h =10 см ниже, чем в первом. Определить скорость V пули, если к первому листу она подлетела, двигаясь горизонтально. Сопротивлением воздуха пренебречь.

1.15. Тело брошено под некоторым углом α к горизонту. Найти этот угол, если горизонтальная дальность s полета тела в четыре раза больше максимальной высоты H траектории.

=45⁰.

1.16. Тело брошено под углом α = 30 к горизонту. Найти тангенциальное а_τ и нормальное а_n ускорения в начальный момент движения.

4,9 м/с²; 8,55 м/с².

1.17. Линейная скорость V₁ точек на окружности вращающегося диска равна 3 м/с. Точки, расположенные на b = 10 см ближе к оси, имеют линейную скорость V₂ = 2 м/с. Определить частоту вращения n диска.

n = (V₁ - V₂) /(2πb) = 1,59 с^-1.

1.18. На цилиндр, который может вращаться около горизонтальной оси, намотана нить. К концу нити привязали грузик и предоставили ему возможность опускаться. Двигаясь равноускоренно, грузик за время t = 3 с опустился на h = 1,5 м. Определить угловое ускорение V цилиндра, если его радиус r =4 см.

ε = 2 h /(rt²) = 8,33 рад/с².

19. Маховик начал вращаться равноускоренно и за промежуток времени t = 10 с достиг частоты вращения n = 300 мин^-1. Определить угловое ускорение  маховика и число N оборотов, которое сделает колесо за это время.

ε = 2π n /(Δt) = 3,14 рад/с².

19. Частица колеблется по закону Х=Аcost. Построить графики: а) функций Х(t),X/dt,d²X/dt²в зависимости отt;b) функцийdX/dt,d²X/dt²в зависимости от Х.

20. Частица совершает гармоническое колебание с амплитудой Aи периодомT. Найти: а) времяt₁, за которое положение частицы меняется от 0 до А/2;b) времяt₂, за которое положение частицы меняется от А/2 до А.

t₁=T/12, t₂=T/6.

19. Шарик подвешен на длинной нити. Один раз его поднимают по вертикали до точки подвеса, другой раз его отклоняют как маятник на небольшой угол. В каком из этих случаев шарик скорее возвратится в начальное положение, если его отпустить?

В первом случае в 1,11 раз быстрее.

19. Частица совершает одномерные гармонические колебания около положения равновесия Х=0. Скорость ее меняется по закону см/с. найти путь, пройденный частицей за первые 10 секунд.

S=1,16 м.

19. Результирующее колебание точки, участвующей в двух колебаниях одного направления, описывается выражением . Найти период биений и циклические частоты₁и₂складываемых колебаний.

Т_Б=1,5 с,₁=77,9 с ^–1и₂=82,1 с ^–1.

19. Частица одновременно участвует в двух взаимно перпендикулярных колебаниях, описываемых уравнениями и. Найдите уравнение движения частицы. Изобразите траекторию и укажите направление движения частицы.

20. Определите длину волны , если расстояние между первой и пятой пучностями стоячей волны равно 32 см.

=16 см.

19. Определите частоту основного тона столба воздуха в открытой с одного конца трубе, если ее длина L=0,85 м. Скорость распространения волны в воздухеV=340 м/c.

=200 Гц.

19. Найти коэффициент затухания и логарифмический декрементматематического маятника, если известно, что за время 100 секунд колебаний механическая энергия маятника уменьшилась в десять раз. Длина маятникаL=0,98 м.

=0,0115 с ^–1,=0,023.

19. Вдоль оси Х распространяется плоская гармоническая волна длиной . Определить расстояниеХ между точками, в которых фазы колебаний отличаются на/2.

Пример 2.1.

Какую скорость может сообщить футболист мячу при ударе, если максимальная сила, с которой он может действовать на мяч, F_MAX =3,510³ H, время удара t₀ = 810 ^–3 c. Считать, что сила во время удара нарастает и спадает по линейному закону (см. рисунок). Масса мяча m = 0,5 кг.

V₂=?

F_MAX=3,510³ H

t₀ = 8·10 ^–3 c

m = 0,5 кг

Решение.

Известно, что изменение импульса тела для переменной силы определяется соотношением (2.27):

. (1)

Поскольку направление удара не меняется, то выбрав координатную ось в направлении удара, уравнение (1) можно записать в скалярной форме:

. (2)

Так как Р₁ равно нулю, то из (2) следует, что

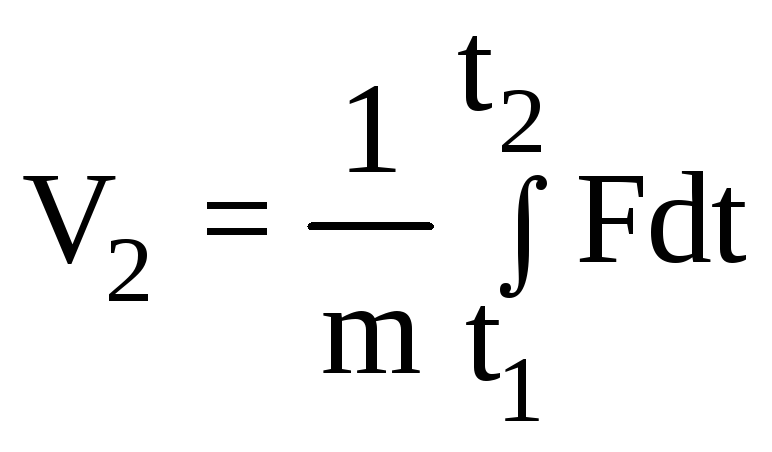. (3)

Используя график, приведенный на рисунке, можно найти аналитическое выражение для закона изменения силы, и проинтегрировать выражение (3), определяющее скорость мяча после удара. Более простое решение имеем, если заметить, что импульс переменной силы численно равен площади под графиком зависимости силы от времени. Вычисляя эту площадь, получим:

.

Подставляя численные значения, найдем V₂ =28м/сек.

Обратим внимание, что при решении учитывалась только одна сила – сила удара футболиста, и не учитывалась сила тяжести. Силой тяжести можно пренебречь, так как её величина ~ 5 Н, что значительно меньше силы удара футболиста по мячу.

Пример 2.2.

Два шарика массами m₁ и m₂ движутся навстречу друг другу по идеально гладкой поверхности со скоростями V₁ и V₂. Определите скорость U шариков после абсолютно неупругого удара.

U=?

m₁, m₂, V₁, V₂

Решение

Рассмотрим механическую систему, образованную двумя сталкивающимися шариками. На систему, как показано на рисунке, действуют силы тяжести m₁g и m₂g, а также силы реакции опоры R₁ и R₂, которые являются внешними силами, таким образом, система не является замкнутой. В соответствии с (2.31) импульс системы не сохраняется. Однако, если рассмотреть два состояния системы, первое – за одно "мгновение" до столкновения, второе – спустя мгновение после столкновения, то изменение импульса будет незначительно, и можно считать, что импульс системы сохранился:

P_І = Р_ІІ, (1)

где P_І = p₁ + р₂ — импульс системы до столкновения (p₁ = m₁V₁, p₂ = m₂V₂). Поскольку абсолютно-неупругим ударом называется взаимодействие, в результате ко­торого тела начинают двигаться вместе (с одинаковой скоростью), то импульс системы после взаимодействия равен

Р_ІІ = (m₁ + m₂)U.

Закон сохранения импульса позволяет записать:

m₁V₁+ m₂V₂=(m₁ + m₂)U. (2)

Проецируя уравнение (2) на ось координат Х получим:

m₁V₁ - m₂V₂ = (m₁ + m₂)U,

откуда:

u=(m₁V₁- m₂V₂)/(m₁+m₂).

Замечание. Знак проекции скорости U шариков после столкновения заранее не определен, в отличие от знака проекций скоростей V₁ и V₂, определяемых с помощью рисунка к задаче. В этом случае рекомендуется знак опустить, знак проекции, а, значит, направление движения шариков после столкновения, укажут вычисления.

Пример 2.3.

На высоте h = 80 м снаряд, летящий горизонтально со скоростью V₀ = 100м/с, разрывается на два равных осколка. Первый осколок через t₁ = 2с падает в эпицентр взрыва. Определить дальность полета второго осколка L₂.

Решение.

L_2=?

h = 80 м , V = 100м/с , m₁=m₂=m/2, t₁ = 2с, L₁=0

На снаряд и осколки (см. рис.) действует внешняя сила тяжести, сообщая им ускорение свободного падения g. Обозначим: V₀₁ и V₀₂ – скорости первого и второго осколка сразу после взрыва, V₁ и V₂ мгновенные скорости осколков в полете, S₁ и S₂ – перемещения осколков, t₁ и t₂ время полета осколков.

Движение первого и второго осколков описывается уравнениями кинематики:

В проекциях на оси координат записанная система включает в себя следующие уравнения:

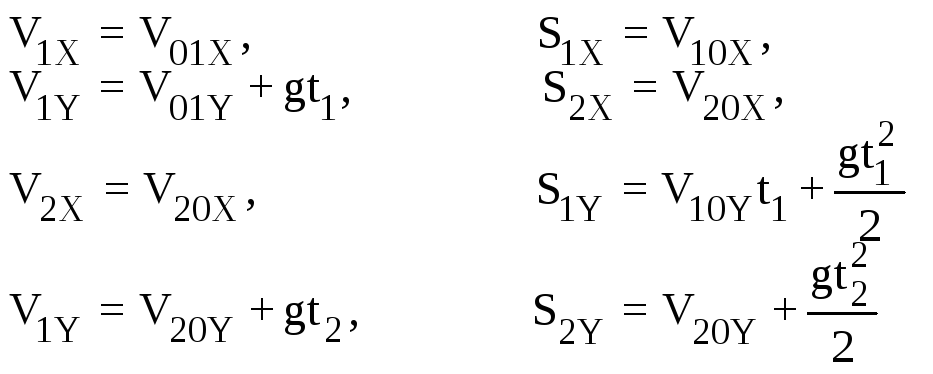
Обращаясь к рисунку заметим, что S_1X=0 следовательно V_0X=0; S_1Y= S_2Y=h; S_2X=L₂. систему уравнений можно переписать следующим образом:

Итак, дальность полета второго осколка равна

. (1)

Из последнего уравнения системы можно найти два значения для времени t₂ полета второго осколка:

.

Очевидно, что условию задачи удовлетворяет положительные решение, равное

. (2)

Четвертое уравнение системы позволяет определить начальную скорость первого осколка:

(3)

Необходимые для дальнейших расчетов V_02Х и V_1Y найдем с помощью закона сохранения импульса. Вообще говоря, снаряд и осколки не образуют замкнутую механическую систему, поскольку действует внешняя сила тяжести. Однако, импульс системы остается постоянным в течение бесконечно малого промежутка времени до взрыва и непосредственно после него.

По закону сохранения импульса можно записать:

P_І = Р_ІІ,

где Р_I=P₀, Р_ІІ = р₁+р₂, p₁ – импульс первого, a p₂ – импульс второго осколка. Или окончательно:

P₀= р₁+р_2, mV₀=mV₀₁/2+mV₀₂/2.(4)

На рисунке к задаче показаны импульсы снаряда P_І и осколков p_{1 и} p₂. В проекциях на оси координат уравнение (4) записывается так:

откуда:

V_02x = 2V, V_02y = – V_01y. (5)

Подставляя численные значения в формулу (3) получим:

V_01y= 30 (м/с).

Наконец, используя (1), (2) и (5), найдем дальность полета L₂:

L₂=1600 (м).

Решение задач по динамике движения материальной точки по окружности

Пример 2.4.

Определить угол между вертикальной осью конического маятника и нитью, если тело движется с постоянной угловой скоростью . Длина невесомой нити подвеса L.

Решение

=?

, L, g=9,8 м/с²

Пусть масса конического маятника равна m. Движение материальной точки происходит в горизонтальной плоскости под действием силы натяжения нити Т и силы тяжести mg (см. рисунок).

Основной закон динамики для данной задачи имеет вид:

ma = Т + mg. (1)

Выберем начало системы координат в центре движущегося по окружности тела так, чтобы ось Х проходила через центр окружности, а ось Y направим вверх. Проецируя уравнение (1) на оси, имеем:

(2)

Нормальное ускорение материальной точки а_n = ²r. Из чертежа следует, что радиус траектории маятника r=ОМ равен r=Lsin, где L=МВ – длина подвеса. Используя дополнительные соотношения, преобразуем уравнения системы (2):

(3)

Из уравнений (3) следует:

cos = g/²L,

или

 = arccos(g/²L).

Пример 2.5.

На веревке длиной R = 1м висит груз массой m = 5 кг. Максимальное натяжение, которое может выдержать веревка, T_MAX = 60 Н. Оборвется ли веревка, если ее отклонить на угол  = 30? На какой максимальный угол можно отклонить веревку, чтобы она не разорвалась?

MAX=? ОА=R=1м, m=5 кг, TMAX=60 H, =30

Решение.

На груз m действуют две силы: сила тяжести mg и сила натяжения Т. Основной закон динамики принимает вид:

ma = mg + Т. (1)

Выберем начало системы координат в центре движущегося по окружности тела так, чтобы ось Y проходила через центр окружности, а ось Х направим по касательной.

Проецируя уравнение (1) на оси Y и X имеем:

(2)

Ускорение а_х, входящее во второе уравнение системы (2) представляет собой тангенциальное ускорение и указывает, что модуль скорости движущегося тела меняется с течением времени. Сила натяжения Т в точке А определяется первым из уравнений (2):

(3)

Ускорение a_Y, есть нормальное или центростремительное, ускорение а_n. Очевидно, что максимальное натяжение веревка испытывает в точке А, так как в этой точке тело имеет максимальную скорость, а значит – максимальное нормальное ускорение. Используя выражение a_Y=а_n=V²/R для нормального ускорения, преобразуем уравнение (3):

(4)

Скорость тела в точке А можно определить с помощью закона сохранения механической энергии. В точке наибольшего отклонения полная механическая энергия – это потенциальная энергия е_П = mgh, где h = R(1- соs). В точке А механическая энергия равна кинетической (за нулевой уровень потенциальной энергии удобно принять уровень соответствующий нижней точке А). Уравнение закона сохранения энергии запишем так:

.

Откуда получим, что квадрат скорости с точке А равен

. (5)

Подставляя в (4) выражение (5) получим окончательно для силы натяжения:

. (6)

Подставляя в (6) максимальное значение силы Т=Т_max можно определить угол при котором веревка оборвется, т. к. достигается предельное усилие. Расчеты дают что _max=45.

Итак, если веревку отклонить на 30°, то она не оборвется.

Пример 2.6.

Тело скатывается с вершины гладкой сферической поверхности радиуса R. Найти, при какой скорости тело оторвется от поверхности. Считать, что трение отсутствует.

Решение.

H=? R =0

На скользящее тело действуют сила тяжести mg и сила N нормальной реакции полусферы. Уравнение движения имеет вид

. (1)

Направим ось Х по касательной поверхности полусферы, ось Y – радиально в направлении ее центра. Проецируя уравнение (1) на оси получим:

Преобразуем полученные уравнения.

(3)

Если учесть, что время движения dt может быть вычислено по формуле dt=dℓ/V, где dℓ=Rd, то первое уравнение приводится к следующему виду

.

Интегрируя последнее по V и , получим соотношение

. (4)

В момент отрыва тела от полусферы реакция опоры обращается в ноль, и второе из уравнений (3) принимает вид

(5)

исключив  из соотношений (4) и (5) найдем

.

Пример 2.7.

Найти максимальную разность между силами натяжения нити при вращении в вертикальной плоскости шарика массой m на невесомой нити.

Решение

(Т1-Т2)МАХ=? m

На шарик действуют две силы: сила натяжения Т и сила тяжести mg. Уравнение движения (второй закон Ньютона) запишется так:

. (1)

Для нахождения максимальной разности между силами натяжения, возникающими при вращении шарика, вычислим силы натяжение нити в точках 1 и 2.

Для положения 1 уравнение движения в проекции на оси координат "1" запишется в виде:

, (2)

где .

Аналогично, в положении 2 для проекций в системе координат "2" имеем :

. (3)

так как , то из (2) и (3) имеем

(4)

Разность определим из закона сохранения энергии. Если выбрать за нулевой уровень отсчета потенциальной энергии уровень точки 1, то можно записать, что

.

Следовательно,

. (5)

Подставляя (5) в соотношение (4) имеем окончательно

.

Пример 2.8.

Вал в виде сплошного цилиндра массой m=10 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой m₁=2 кг. С каким ускорением a будет опускаться гиря, если её предоставить самой себе.

a=?

m=10 кг, m₁=2 кг

Решение

В задаче участвуют два тела, совершающие различные движения: тело m₁ движется прямолинейно, вал – вращается. Уравнения движения имеют следующий вид:

, (1)

в системе уравнений (1) введены обозначения: а_ – тангенциальное ускорение точек на периферии вала, Т – сила натяжения шнура, r – радиус вала, М – момент, вращающий вал, а – ускорение тела m₁.

Момент, вращающий вал равен ,J – момент инерции вала относительно геометрической оси. Рассматривая вал как однородный цилиндр, считаем, что его момент инерции равен J = 1/2m₁r².

Определим направление векторных величин (по правилу буравчика) и выбрав направление осей координат как показано на рисунке запишем систему (1) в проекциях.

(2)

При условии, что шнур нерастяжим и отсутствует его скольжение по поверхности вала тангенциальное ускорение а_ по модулю равно поступательному ускорению а груза m₁: а_=а. С учетом дополнительных соотношений уравнения системы (1) примут вид:

(3) Решая систему относительно ускорения a получим:

.

Пример 11.

Через блок в виде диска, имеющий массу m=80г, перекинута тонкая гибкая нить, к концам которой подвешены грузы массами m₁=100г и m₂=200г. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением пренебречь.

Решение.

а1, а2=? m=80 г=810–2 кг m1=100 г =10–1 кг m2=200 г=210–1 кг

Рассматриваемая в задаче система состоит из двух движущихся поступательно грузов и одного вращающегося диска. На каждый из грузов действует две силы: сила тяжести mg, направленная вниз, и силаТнатяжения нити, направленная вверх. Запишем законы поступательного и вращательного движения этих тел.

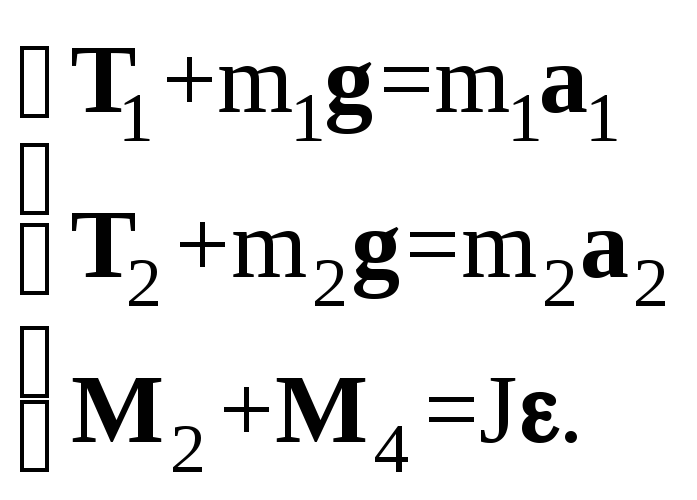(1)

Результирующий вращающий момент, приложенный к диску, равен

М=М₂+М₄=[R₁,T₂]+[R₂,T₄],

R₁иR₂– радиус-векторы точек приложения сил натяжения нитиT₂иT₄. Предположим, чтоm₂>m₁, поэтому ускорения грузов будет направлено, как показано на рисунке. Выберем произвольное направление осей координат (например, как на рисунке) и запишем систему уравнений в проекциях.

(2)

При условии, что нить нерастяжима, отсутствует ее скольжение по поверхности диска, тангенциальное ускорение точек на поверхности диска а_по модулю равно поступательному ускорениюагрузов: а_=а. Угловое ускорение диска связано с линейным ускорением грузов соотношением; в скалярной форме. Пренебрегая массой нити приходим к выводу, что силы натяжения Т₁и Т₂равны по величине. Учтем также, что момент инерции дискаJ=mr²/2. С учетом приведенных дополнительных соотношений система (2) принимает вид:

Решая полученную систему, получим

.

После подстановки числовых значений имеем