1.6. Нормальное, тангенциальное и полное ускорения

Взаимосвязь угловых и линейных характеристик можно рассмотреть на основе общих соображений. Пусть V мгновенная линейная скорость материальной точки, движущейся по окружности,  – ее угловая скорость. Введем единичный вектор касательной , связанный с движущейся материальной точкой. Тогда скорость V можно записать так:

,

здесь V_=V – проекция вектора скорости на направление вектора касательной. Дифференцируя (1.25) по времени, получим:

.

Преобразуем второй член последнего соотношения:

.

Как видно из рисунка (1.5)

.

Направление d/dℓ совпадает с направлением вектора внутренней нормалиn. Окончательно (1.26) запишем следующим образом:

.

В соотношении (1.29) первое слагаемое представляет собой тангенциальной ускорение а_, второе – нормальное а_Н или центростремительное ускорение. Таким образом,

:

полное ускорение движущейся точки равно векторной сумме нормального и тангенциального ускорений. Модуль полного ускорения определяется соотношением:

Воспользуемся формулой Эйлера (1.21): . Дифференцируя по времени (1.31), имеем:

,

где d/dt= угловое ускорение, dR/dt=V – мгновенная линейная скорость материальной точки.

Рис. 1.6. V – мгновенная линейная скорость, a – тангенциальное, an – нормальное и a – полное ускорение частицы. О – центр касательной окружности радиусом R, n – внешняя нормаль к траектории движения

Из рисунка 1.6 видно, что множитель представляет собой тангенциальное ускорение, а– нормальное или центростремительное ускорение.

Таким образом (1.32) можно привести к виду: . (1.32а)

1.7. Кинематика произвольного криволинейного движения

В общем случае неравномерного движения материальной точки по криволинейной траектории, ускорение а равно сумме нормального а_Н (центростремительного) и тангенциального а_ ускорений:

.

Вектор тангенциального ускорения α_τ направлен по касательной к траектории, векторα_Н – по нормали к траектории (центростремительное ускорение);α_nхарактеризует изменение направления скорости со временем,а_– характеризует изменение модуля скорости.

Величины α_nиα_τопределяют характер движения материальной точки.

1. α_Н=0,α_τ=0 – прямолинейное равномерное движение,

2. α_Н=0,α_τ=const – прямолинейное равнопеременное движение,

3. α_Н=const0,α_τ=0 – движение по окружности с постоянной по величине скоростью,

4. α_Н0,α_τ=const, приR=const равнопеременное движение по окружности,

5. α_Н0,α_τ0 – криволинейное неравномерное движение.

1.8. Кинематика колебательного движения

• Колебания – это движения или процессы, обладающие той или иной степенью повторяемости во времени.

Колебания широко распространены в природе и имеют место в самых разнообразных явлениях, например, качание маятника пружинных часов, мигание индикатора таймера, изменение значения переменного тока, величины напряжения на обкладках конденсатора, включенного в колебательный контур и т. п. Повторяющиеся процессы протекают внутри живых организмов, например, биение сердца, чередование промежутков сна и бодрствования, ритмы, сопровождающие работу человеческого мозга. Таким образом, колебания присутствуют как в живой, так и в неживой природе; в микроскопических и макроскопических процессах.

Важнейшая особенность колебательного движения состоит в том, что оно происходит в системах, занимающих ограниченную часть пространства. Так, совершая колебательное механическое движение, система движется около некоторого положения равновесия, но энергия системы не выходит за пределы границ системы. Колеблющаяся величина, заключена в некоторый интервал, содержащий ее среднее значение. Несмотря на качественное различие тех или иных колебательных процессов, все они могут быть описаны одними и теми же количественными законами.

• Свободные, или собственные колебания – это колебания, которые происходят в системе, выведенной из состояния равновесия и предоставленной самой себе.

• Гармоническими колебаниями называют колебания, при которых колеблющаяся величина изменяется во времени по закону синуса или косинуса. Гармонические колебания представляют собой простейшие колебания.

Уравнение гармонически меняющейся величины  может быть как с помощью функции синуса, так и с помощью функции косинуса следующим образом:

.

В формулу (1.33) входят следующие величины:

• Амплитуда колебаний А – наибольшее значение колеблющейся величины . Из (1.33) следует, что А>0.

• Фаза колебаний – – аргумент функции синуса или косинуса в уравнении гармонического колебания.

• Начальная фаза колебаний – 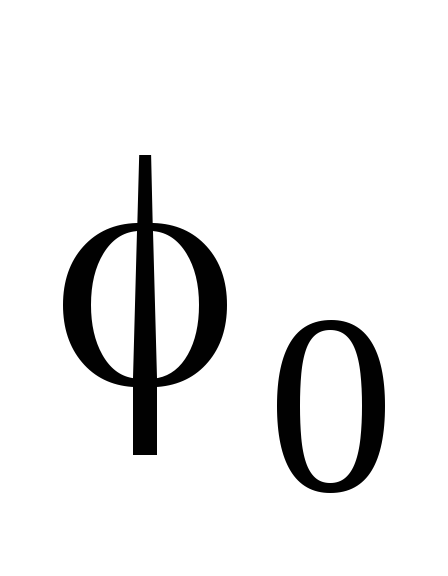значение фазы в момент времени t=0.

При необходимости, переход от функции синуса к функции косинуса осуществляется по формулам приведения, при этом изменяется начальная фаза колебаний. Например, в формулах (1.33) .

• Период колебаний Т – это время, за которое совершается одно полное колебание.

• Можно говорить, что период – это наименьший промежуток времени, по истечении которого колеблющаяся величина  имеет то же самое значение и ту же скорость изменения.

• Частота колебаний  (n, или f) – величина обратная периоду колебаний

.

• Круговая, или циклическая, частота  связана с частотой  соотношением

.

Измеряется циклическая частота в с ^–1. Она показывает, какое число колебаний происходит за 2 секунд.

Используя определение периодичной функции – F(х)=F(х+Т), запишем:

.

Поскольку функция имеетпериод 2, то сравнение фаз колебаний позволяет установить связь периода колебаний с циклической частотой:

,

отсюда следует, что

.

Частота показывает, какое число колебаний совершается за единицу времени (секунду). Измеряется частота в герцах: . 1 Гц – это такая частота, при которой в единицу времени совершается одно колебание.

Скорость изменения V и ускорение – a колеблющейся величины  определяется обычным образом (по формулам (1.4) и (1.7)):

Начальную фазу колебаний, можно определить с помощью первого из уравнений (1.33) по известным начальным условиям ₀, V₀:

и .

Откуда следует:

.

Амплитуду гармонически колеблющейся величины можно вычислить по формуле: