2. 10.1.2. Преобразования Лоренца

Преобразования координат и времени при переходе от одной ИСО к другой в СТО называют преобразованиями Лоренца. Классический закон преобразование скоростей по Галилею (*) противоречит постулату о постоянстве скорости света. Действительно, при V₀=c закон Галилея дает для скорости света в неподвижной системе отсчета значение равное 2с. Очевидно, что при скоростях, сравнимых со скоростью света, преобразования Галилея не применимы и должны быть заменены другими. Свойства однородности и изотропности пространства требуют, чтобы эти преобразования были линейными.

Будем искать закон преобразования координат х и времени t при переходе от неподвижной системы отсчета К к подвижной К в виде линейной комбинации x и t:

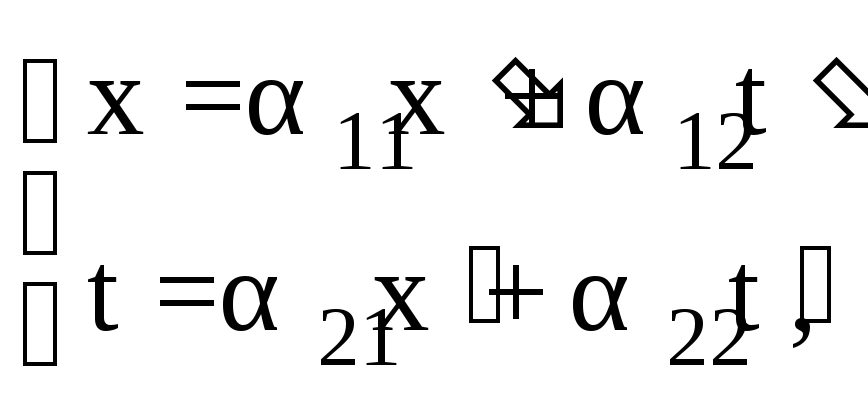
здесь коэффициенты зависят от скоростиV₀ относительного движения систем отсчета К и К.

Пусть в начальный момент времени начала координат 0 и 0 обеих СО совпадают (см. рис. 10.3). В момент времени t=t=0 из точки 0 (0) вдоль осей x и x испущен световой сигнал. За время t, (t) он достигнет некоторой точки Р с координатами

.

Подставим соотношения (10.3) в (10.2) и умножим второе из них на с:

.

Из (10.4) следует

.

Рис. 10.3. Неподвижная (x,y,z,o) и подвижная (x,y,z,o) системы отсчета

Если световой сигнал в начальный момент времени был направлен против осей x и х, то координаты точки P, до которой дойдет сигнал спустя время t (t) будут равны:

.

Подставим (10.6) в (10.2) и умножив второе уравнение на с получим:

.

.

Складывая и вычитая (10.5) и (10.8), получим:

.

Точка Оначала координат системы Кв системе К имеет координату x=V₀t, а в системе Кона равна нулю (x=0), подставляя эти значения в (10.2) имеем:

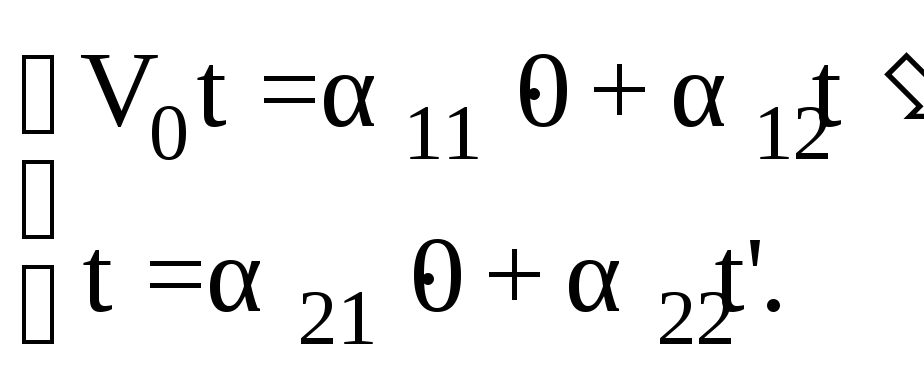
Из последних соотношений следует

.

Учитывая, что ₁₁=₂₂имеем

.

Подставляя полученное выражение в (10.11), получим:

.

Используя соотношения (10.9) – (10.13), перепишем формулу (10.2) следующим образом:

.

Используя очевидные равенства:

,

можно записать

.

Выразим xиtчерезxиt, и используя соотношения (10.14) запишем:

=

=.

По теореме о тождественно равных многочленах, запишем равенство коэффициентов при соответствующих переменных:

.

Отсюда получаем:

.

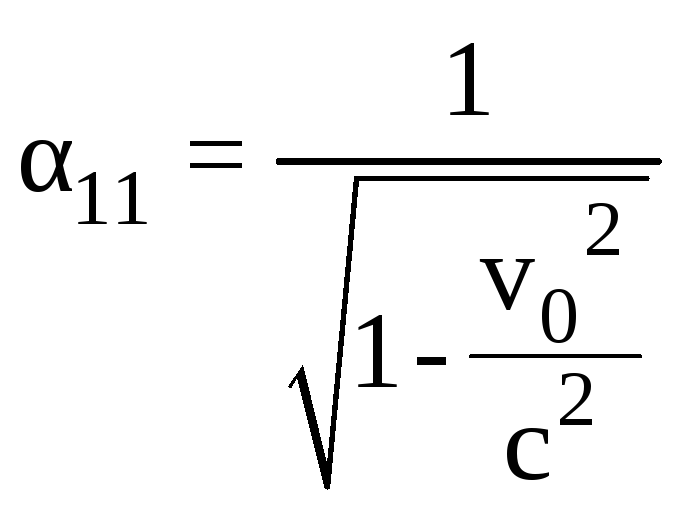Для удобства записи формул СТО отношение V₀/cобозначают через, с учетом этого соотношение (10.16) можно записывать так:

.

Подставив (10.16) в (10.14), получим формулы преобразований для координаты xи времениt:

Соотношения (10.17) – есть искомые преобразования Лоренца для координат и времени.

Легко заметить, что при малых скоростях, V₀<<c, соотношения (10.17) переходят в известные соотношения Галилея (2.4) для преобразования координат и времени:

С формальной точки зрения соотношения (10.17) имеют смысл при обязательном условии, что подкоренное выражение больше нуля. Отсюда следует, что скорость V₀не может превышать и даже равняться скорости света.

Инвариантность интервала

Предположим, что в инерциальной системе отсчета К (x₁, y₁, z₁, сt₁) – координаты первого события, x₂, y₂, z₂, сt₂ – координаты второго события, величина

называется интервалом между этими событиями.

Обозначив расстояние между точками, в которых происходит событие через L₁₂, а длительность события t₁₂=t₂–t₁, получим для интервала

.

Легко показать, что интервал – инвариантная величина, то есть его величина во всех инерциальных системах отсчета одна и та же. Для доказательства запишем интервал s₁₂ в системе К и s₁₂ в системе К:

.

Воспользуемся формулами (10.18), запишем:

.

Для интервала (s)² имеем:

Числитель полученного выражения преобразуем отдельно:

.

Возвращаясь к предыдущему соотношению, получим:

Таким образом, интервал s – инвариант при переходе от одной ИСО к другой.