1. 9.7.2. Закон Архимеда.

На поверхность твердого тела, опущенного в жидкость (газ), действуют силы давления. Эти силы увеличиваются с глубиной погружения, поэтому на нижнюю часть тела будет действовать со стороны жидкости большая сила давления, чем на верхнюю. Равнодействующая сил давления представляет собой выталкивающую силу, или силу Архимеда.

Для нахождения величины силы Архимеда мысленно заменим полностью погруженное в жидкость тело жидкостью в объеме тела (рис. 9.11).

Ясно, что выделенный объем жидкости будет неподвижен относительно остальной жидкости. На него со стороны окружающей жидкости будет действовать такая же выталкивающей сила, как и на погруженное тело.

Рис. 9.11 К выводу закона Архимеда

По третьему закону Ньютона, выделенный объем жидкости будет действовать на окружающую жидкость с той же по модулю, но противоположно направленной силой – своим весом. Проведенные рассуждения позволяют сформулировать закон Архимеда.

• Закон Архимеда: на тело, погруженное в жидкость (или газ), действует выталкивающая сила, равная весу вытесненной жидкости:

,

где ρ – плотность среды, в которую погружено тело, V – вытесненный телом объем среды.

Подчеркнем, что в законе Архимеда говорится о весе вытесненной жидкости. Как известно, вес тела не всегда совпадает с силой тяжести, действующей на него. Теперь ясно, что выталкивающая сила отсутствует в состоянии невесомости, например, в свободно падающем сосуде с жидкостью, и в космическом корабле, двигатели которого не работают.

Если часть поверхности тела плотно прилегает к стенке или дну сосуда так, что между ними нет прослойки жидкости, то закон Архимеда неприменим. Эта ситуация изображена на рис. 9.12. Брусок не всплывает, т.к. со стороны воды на него действует сила, прижимающая его ко дну, а не вы­талкивающая вверх.

Рис.9.12. Отсутствие выталкивающей силы

Приведенная формулировка закона Архимеда остается справедливой в случаях, когда тело плавает в жидкости (в том числе в движущейся) или частично опущено в нее через свободную поверхность жидкости. Линия действия выталкивающей силы будет проходить через центр тяжести вытесненного объема жидкости, который может не совпадать с центром тяжести тела.

Пример 9.1.

Тонкий однородный стержень, укрепленный вверху шарнирно, опущен в воду так, что две трети стержня оказались в воде. Определите плотность материала стержня, считая плотность воды известной.

Решение

=? L1=2L/3 B=10 3 кг/м3 

На стержень действуют сила тяжести стержня mg, приложенная в центре стержня, сила Архимеда F_A, приложенная в центре погруженной в воду части стержня, и сила N реакции шарнира, приложенная в точке А шарнира.

Запишем условие равновесия стержня:

,

или в подробной записи

. (1)

Радиус-векторы R_gиR_Aпоказаны на рисунке светлыми стрелками. Проецируя уравнение на ось z, и учитывая, что , так как R_N =0, получим:

(2)

Пусть S – площадь поперечного сечения стержня,  – плотность материала стержня, тогда масса стержня m=ρLS, а сила Архимеда

.

Подставляя выражения для m и F_A в уравнение (2), после преобразований получим:

, или =888 кг/м³.

Пример 9.2.

Вода движется по трубе переменного сечения, пусть V₁=15 см/с и S₁/S₂= 4 . Каково различие в высоте воды в вертикальных трубках?

d=?

V₁=15 cм/c, S₁/S₂= 4

Решение

Воспользуемся формулами (9.10) и (9.11), запишем

p₁-p₂= ρgd=ρ(V₂² – V₁²)/2,

откуда следует:

d=(V₂² – V₁²)/2g.

Жидкость несжимаема, значит поток, проходящий через малое сечение трубы, такой же, как и поток, проходящий через большое сечение, отсюда: S₁V₁=S₂V_2. Найдем V₂.

Подставляя значения V₁ и V₂ в выражение для d, находим:

.
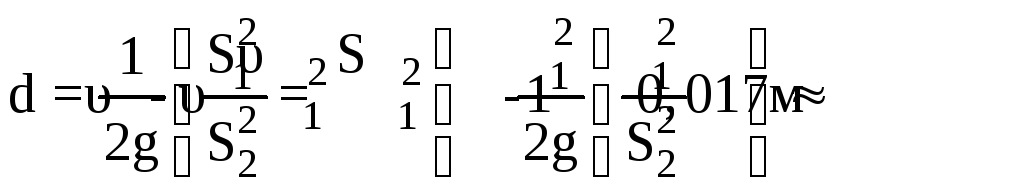