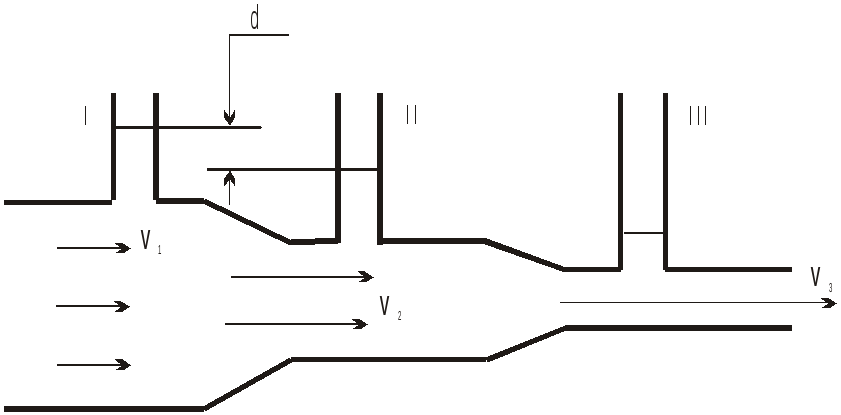
10. 9.4. Горизонтальный поток жидкости

Рассмотрим (рис. 9.6) прохождение жидкости через горизонтальную трубу (трубку тока), имеющую переменное сечение. Пусть сечения S_I и S_II находятся на одной высоте h=h₁=h₂. Уравнение Бернулли в этом случае принимает вид:

.

Из уравнения непрерывности струи следует, что скорость течения жидкости в местах сужения больше (V₃>V₂>V₁), а, значит, динамическое давление в этих местах больше.

Рис. 9.6. Горизонтальный поток

Из соотношения (9.10) следует, что внешнее давление в этих сечениях, равное сумме атмосферного и гидростатического давлений, напротив меньше, что соответствует меньшей высоте поднятия жидкости в трубке. Разность d уровней, на которые поднимается жидкость в трубках I, II и III может служить для измерения разности давлений в различных сечениях потока

.

11. 9.5. Подъемная сила

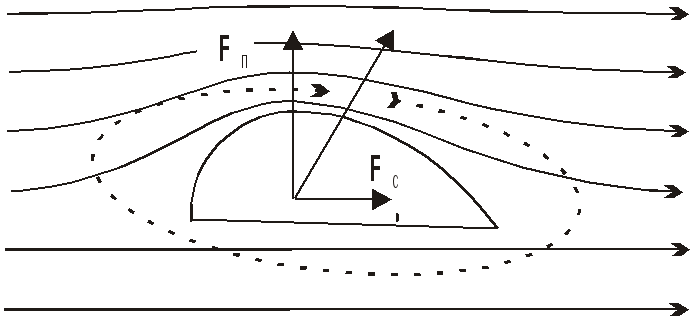
Подъемная сила возникает при обтекании несимметричного тела потоками газа или жидкости. На рисунке 9.7 показаны линии тока жидкости на полуцилиндре, ось которого перпендикулярна плоскости чертежа. Очевидно, скорость течения над полуцилиндром выше, чем под ним. Уравнение Бернулли позволяет заключить, что давление на нижнюю поверхность полуцилиндра больше, чем на верхнюю. Разность давлений обуславливает разность сил давления и, в конечном счете, вызывает подъемную силу F_п.

Рис. 9.7. К возникновению подъемной силы

Аналогичную картину образуют линии тока около крыла самолета, схематически изображенного на рисунке 9.8. Не входя в детали обтекания тел реальными жидкостями и газами, отметим, что теоретические исследования Н. Жуковского и др. показали важную роль образующихся при этом вихрей. Направление движения вихря показано штриховой линией.

Рис. 9.8. Крыло самолета испытывает подъемную силу, благодаря потому, что Vв>Vн и Pн>Pв

Сложение скорости потока и вихря приводит к тому, что над крылом (верх) скорость потока увеличивается, а под крылом (низ) – уменьшается, при этом V_B>V_H. Формула ( 9.8 ) показывает, что P_H>P_B, т. е. воздух под крылом имеет давление выше, чем воздух над крылом. В результате образуется результирующая сила, направленная вверх, эту силу и называют подъемной силой.

12. 9.6. Течение вязкой жидкости

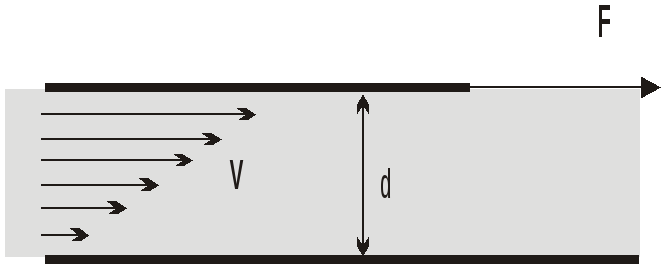
Реальная жидкость обладает трением. Мы можем измерить меру вязкости жидкости следующим образом. Поместим слой жидкости толщиной d между двумя большими параллельными пластинами, как показано на рис. 9.9.

Рис. 9.9. Ламинарное течение вязкой жид­кости

Пусть нижняя пластина закреплена, к верхней – приложена горизонтальная сила F, которая приводит пластину в ускоренное движение. С течением времени верхняя пластина начнет двигаться с постоянной скоростью V; это означает, что сила F уравновешена некоторой силой – силой вязкого трения F_ТР.

Закон, определяющий зависимость величины силы вязкого трения F_ТР от условий, характеризующих движение, был установлен И. Ньютоном и имеет следующий вид:

.

Коэффициент  называют коэффициентом вязкости, или просто вязкостью:

.

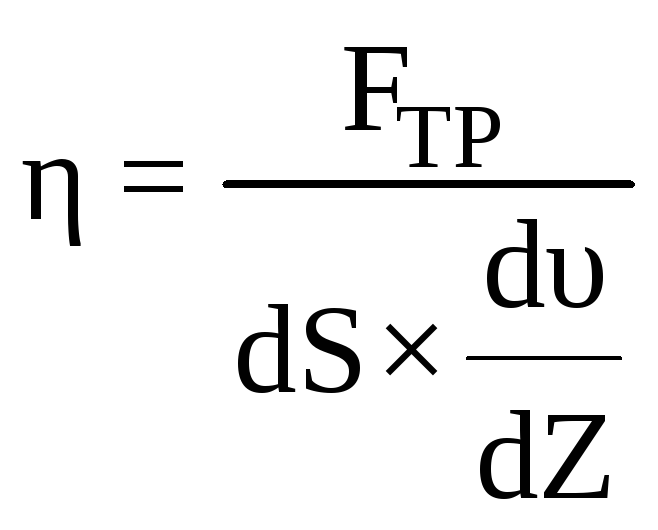Коэффициент вязкости показывает, какая сила действует на единицу площади соприкасающихся слоев при дополнительном условии dυ/dZ=1. Величина dυ/dZ называется градиентом скорости.

Размерность коэффициента вязкости устанавливается так:

.

Величина коэффициента вязкости η различна: он мал для воздуха (1,8·10^-5 Па·с) и значительно больше для машинного масла (0,99 Па·с).