7.6. Вынужденные колебания

• Вынужденные колебания – это колебания, происходящие в системе при воздействии на нее периодической силы.

Рассмотрим колебания системы, подверженной воздействию силы тяжести mg, силы упругости F_УПР, внешней периодической силы F = F₀cost. Во избежание решений, обращающихся в бесконечность, будем учитывать силу вязкого трения F_ТР = – rV, всегда присутствующую при движении в газе или жидкости.

Уравнение второго закона Ньютона для колеблющегося маятника с вязким трением имеет вид:

.

Рассуждения, аналогичные проведенным в предыдущем разделе, приводят в одномерном случае к дифференциальному уравнению:

,

где введены следующие обозначения: m – масса колеблющегося тела, k – коэффициент упругости пружины, r – коэффициент сопротивления, f₀=F₀/m и, наконец,

, .

Решение дифференциального уравнения (7.33), которое представляет собой уравнение второго порядка с постоянными коэффициентами, неоднородное, представляет собой сумму общего решения х₁ однородного уравнения

,

и какого-нибудь частного решения х₂ неоднородного уравнения (7.33).

Общее решение уравнения (7.34), представляющего собой уравнение колебаний в системе с трением, найдено в предыдущем разделе:

,

где , А₀ и  – некоторые постоянные.

Частное решение уравнения (7.33) имеет следующий вид:

.

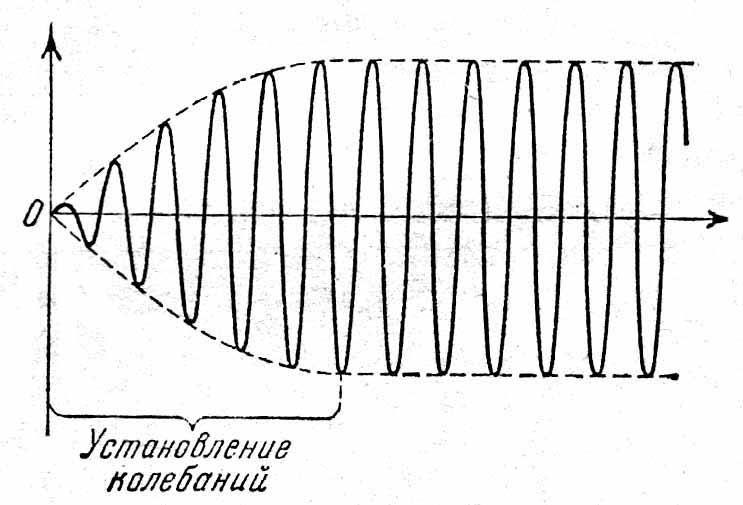
Обратим внимание на то, что решение х₁ за счет множителя e ^–t экспоненциально затухает со временем. Оно описывает колебания на их начальной стадии и соответствует времени установления колебаний, в нем присутствует частота собственных колебаний маятника с трением: .

Частное решение – х₂ – зависит от частоты ₀ свободных колебаний и частоты  вынуждающей силы. Временная зависимость интенсивности вынужденных колебаний графически представлена на рисунке (7.7).

Рис. 7.7. Амплитуда вынужденных колебаний в зависимости от времени

1. 7.7. Резонанс

• Резонансом называют явление резкого увеличения амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к частоте собственных колебаний.

• Вынуждающая сила – внешняя периодическая сила, действующая на колебательную систему.

• Резонансная частота – частота, при которой наступает явление резонанса.

Явление резонанса вызвано зависимостью (см. (7.35)) амплитуды установившихся вынужденных колебаний от частоты внешнего воздействия:

.

Найдем резонансную частоту _РЕЗ для пружинного маятника из условия максимума величины х₂. Очевидно, что х₂ принимает максимальное значение, если знаменатель выражения (7.35) принимает минимальное значение. Условие экстремума знаменателя записывают так:

.

Вычисляя производную, после преобразований получим выражение, позволяющее найти _РЕЗ:

.

Полученное уравнение имеет три корня:

, и.

Очевидно, что не удовлетворяет условию, т. к. частота существенно положительная величина.При каком из корней или выполняется условие минимума, выясним, определяя знак второй производной:

.

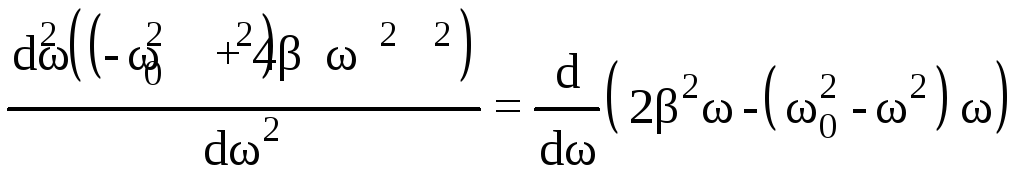При ₁=0 вторая производная отрицательна, что соответствует максимуму знаменателя и минимуму колеблющейся величины х₂. При ₂ знаменатель минимален, значит ₂=_РЕЗ:

.

Подставив значение _РЕЗ в выражение (7.35), найдем выражение для резонансной амплитуды А_РЕЗ:

.

Последнее соотношение указывает на отмеченную ранее необходимость учета сопротивления среды (0), в противном случае резонансная амплитуда обращалась бы в бесконечность.

При 0 выражение (7.38) принимает вид

,

или

,

что соответствует статическому растяжению пружины в соответствии с законом Гука.

При стремлении частоты вынуждающей силы к бесконечности амплитуда вынужденных колебаний стремится к нулю. Зависимость амплитуды от частоты в виде так называемой резонансной кривой представлена на рисунке 7.8.

Рис. 7.8. Резонансная кривая. Зависимость отношения амплитуды вынужденных колебаний к величине статического смещения от безразмерной частоты . Использованы относительные единицы:  = /P и N = A/AР

Из формулы (7.35) вытекает также, что фазы вынуждающей силы и вынужденных колебаний отличаются друг от друга: вынужденные колебания отстают по фазе от вынуждающей силы на величину

,

заключенную в пределах от 0 до  (см. рис. 7.9).

Рис. 7.9. Зависимость сдвига фаз  от относительной частоты   /P при различных значениях 

Как видно из приведенного рисунка, при малой частоте вынуждающей силы и при малом затухании сдвиг фаз стремится к нулю, т. е. колебания по фазе совпадают с фазой вынуждающей силы; при высоких частотах сдвиг фаз составляет  – смещение и сила находятся в противофазе и, наконец, при резонансе сдвиг фаз близок к /2.