
- •Лекционный блок
- •Глава 1. Кинематика
- •1.1. Основные понятия
- •1.2. Скорость и ускорение
- •1.3. Равномерное и равнопеременное движение
- •1.4. Кинематика движения по окружности
- •Взаимосвязь угловых и линейных характеристик при движении по окружности
- •1.6. Нормальное, тангенциальное и полное ускорения
- •1.7. Кинематика произвольного криволинейного движения
- •1.8. Кинематика колебательного движения
- •1.8.1. Сложение колебаний одного направления
- •1.8.2. Биения
- •1.8.3. Сложение взаимно перпендикулярных колебаний
- •1.9. Кинематика волнового движения
- •1.9.1. Уравнение плоской волны
- •1.9.2. Общие характеристики волны
- •1.9.3. Распространение, отражение и преломление волн
- •1.9.4. Продольные и поперечные волны
- •1.9.5. Интерференция волн
- •1.9.6. Стоячие волны
- •1.9.7. Эффект Доплера
- •Глава 2. Динамика
- •2.1. Первый закон Ньютона. Инерциальные системы отсчета. Принцип относительности
- •2.1.1. Классический закон сложения скоростей
- •2.2. Второй закон Ньютона
- •2.3. Силы в механике
- •2.3.1. Сила всемирного тяготения
- •2.3.2. Сила тяжести
- •2.3.3. Механическая связь. Реакция связи
- •2.3.4. Сила трения.
- •2.3.6. Сила упругости. Закон Гука
- •2.4. Третий закон Ньютона
- •Материальной точки (тела)
- •2.5.1. Импульс материальной точки
- •2.5.2. Импульс механической системы
- •Динамика движения материальной точки по окружности
- •2.7. Динамика вращательного движения относительно неподвижной оси
- •2.7.1. Момент инерции твердого тела
- •Задачи к главе 2 для самостоятельного решения
- •Глава 3. Статика
- •Глава 4. Работа силы. Мощность
- •4.1. Консервативные и неконсервативные силы в механике
- •4.1.1. Работа силы тяжести
- •4.1.2. Работа силы всемирного тяготения
- •4.1.3. Работа силы упругости
- •Глава 5. Энергия
- •5.1. Потенциальная энергия
- •5.2. Потенциальная энергия и сила поля
- •5.3. Кинетическая энергия поступательного движения
- •5.4. Кинетическая энергия вращательного движения
- •5.5. Полная механическая энергия тела (системы)
- •Глава 6. Законы сохранения
- •6.1. Закон сохранения импульса
- •6.2. Закон сохранения момента импульса
- •6.3. Закон сохранения механической энергии
- •6.3.1. Механическая энергия материальной точки
- •6.3.2. Механическая энергия материальной точки (тела) под воздействием произвольных сил
- •6.3.3. Механическая энергия системы
- •6.3.4. Упругое столкновение
- •Глава 7. Динамика малых колебаний
- •7.1. Пружинный маятник
- •7.2. Физический маятник
- •7.3. Математический маятник
- •7.4. Затухающие колебания
- •Влияние величины сопротивления на характер колебательного движения
- •7.6. Вынужденные колебания
- •7.7. Резонанс
- •Глава 8. Движение в неинерциальной системе отсчета
- •Кинематика движения в неинерциальной системе отсчета
- •8.2. Динамика движения в неинерциальной системе отсчета
- •Глава 9. Элементы гидро- и аэродинамики
- •9.1. Основные понятия
- •9.2. Уравнение Бернулли
- •9.3. Формула Торричелли
- •9.4. Горизонтальный поток жидкости
- •9.5. Подъемная сила
- •9.6. Течение вязкой жидкости
- •9.6.1. Установившаяся скорость
- •9.7. Гидростатика
- •9.7.1. Закон Паскаля. Сообщающиеся сосуды
- •9.7.2. Закон Архимеда.
- •Глава 10. Релятивистская механика
- •10.1. Кинематика специальной теории относительности
- •10.1.1. Интервал
- •10.1.2. Преобразования Лоренца
- •10.1.3. Относительность одновременности
- •10.1.4. Относительность длины
- •10.1.5. Относительность длительности событий
- •10.1.6. Релятивистское преобразование скоростей
- •10.1.7. Релятивистское преобразование ускорений
- •10.1.8. Релятивистский эффект Доплера
- •10.2. Динамика специальной теории относительности
- •10.2.1. Релятивистский импульс
- •10.2.2. Основное уравнение динамики сто
- •10.2.3. Релятивистское выражение для энергии
- •10.2.4. Взаимосвязь массы и энергии
- •10.2.5. Связь между энергией и импульсом тела
- •Соотношения (10.46) и (10.52) показывают, что энергия тела и его импульс зависят от системы отсчета, принятой в данном конкретном случае. Покажем, что величина
- •Примеры решения задач
- •Примеры решения задач по кинематике криволинейного движения
- •Примерная схема решения задач по кинематике колебаний
- •Задачи к главе I для самостоятельного решения
- •Задачи к главе 2 для самостоятельного решения
- •Задачи к главе 3 для самостоятельного решения
- •Задачи к главе 6 для самостоятельного решения
- •Задачи к главе семь для самостоятельного решения
- •Задачи к главе 9 для самостоятельного решения
- •Задачи к главе 10 для самостоятельного решения
1.3. Равномерное и равнопеременное движение
Существует несколько классификаций движения по тому или иному признаку. Так, механическое движение подразделяют на равномерное и неравномерное.
Равномерное движение – можно определить несколькими способами:
равномерное движение – это движение, при котором за любые равные промежутки времени материальная точка (тело) совершает одинаковые перемещения,
равномерное движение – это движение с постоянной скоростью,
равномерное движение – это движение, при котором ускорение равно нулю.
Неравномерным движением материальной точки называют движение, при котором скорость меняется с течением времени.
Одной из характеристик неравномерного движения является ускорение. Простейший вид неравномерного движения – равнопеременное движение.
Равнопеременное движение– это:
движение, при котором за любые равные промежутки времени скорость точки (тела) изменяется на одну и ту же величину,
движение, при котором ускорение аматериальной точки остается постоянным.
Интегрируя соотношения, определяющие мгновенную скорость (1.4) и мгновенное ускорение (1.7), можно получить основные законы кинематики материальной точки.
Законыкинематики:
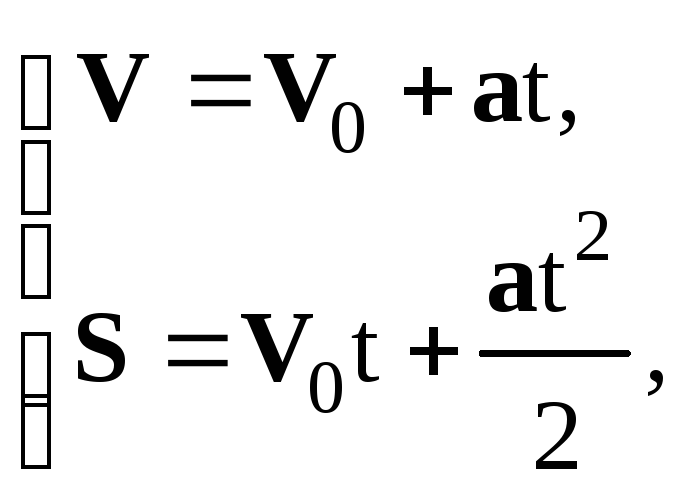
первое из уравнений системы называется законом изменения скорости – V=V(t), второе – законом движения –S=S(t);V0– начальная скорость, т. е. скорость материальной точки в момент времениt=0,a– ее ускорение.
Законы (1.8) включают в себя два частных случая:
Равнопеременное движение без начальной скорости: начальная скорость V0 равна нулю, ускорение а не равно нулю и
Равномерное движение со скоростью V0 и ускорением а равным нулю. Законы кинематики в этих случаях принимают следующий вид:
|
|
и |
|
В координатной записи уравнения (1.8) имеют следующий вид:
 (1.8а)
(1.8а)
Закон движения – S=S(t) позволяет определить координаты движущейся материальной точки в произвольный момент времени. Учитывая, что S = r1 – r0 запишем:
![]() .
.
Из последнего соотношения следует, что координата Х в момент t равна
![]() .
.
Механические движения различаются также по виду траекторий: прямолинейное, вращательное и криволинейное. Если модуль перемещения dr=dr по величине равен пройденному пути ds, то материальная точка движется по прямой линии. В этом случае модуль мгновенной скорости равен первой производной пути по времени:
![]() .
.
Соотношение (1.9) – основное при решении задач по кинематике. Интегрируя его, можно найти длину пути, пройденного телом за время от t1 до t2:
 .
.
Для равномерного движения со скоростью V=const из (1.10) следует:
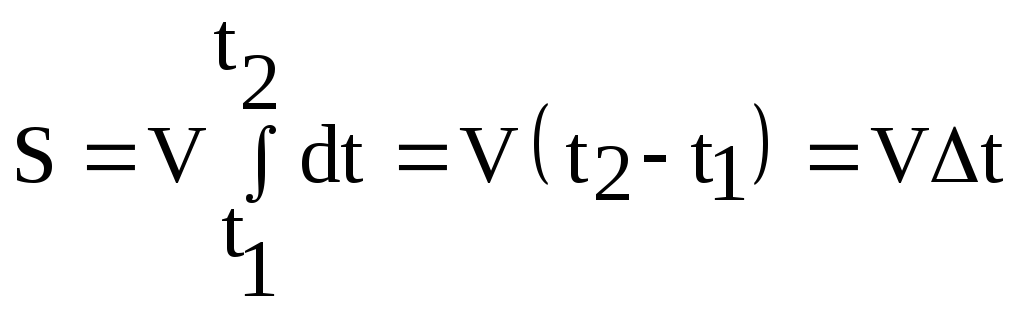 ,
,
здесь t=(t2-t1) – время движения.
1.4. Кинематика движения по окружности
Если материальная точка М движется по окружности (см. рис. 1.3), то ее положение определяют вектором угла d1, который образован ее радиус-вектором R с некоторой, произвольно выбранной осью Х.
|
|
Рис.1. 3. На рисунке обозначены: V – линейная скорость, d – угол поворота радиус-вектора точки за время dt, d – вектор угла поворота, – угловая скорость |
Вектор угла d можно определить следующим образом:
![]() ,
,
здесь eZ – единичный вектор оси вращения Z. Заметим, что модуль радиус-вектора материальной точки равен радиусу окружности, по которой она движется: R=R.
При решении задач удобно выбрать направление оси Х так, чтобы она проходила через начальное положение движущейся точки. Модуль вектора угла d численно равен углу поворота радиус-вектора, измеренному в радианах; направление d определяется по одной из альтернативных (Б.I) формулировок правила буравчика (правого винта).
Правилобуравчика(Б.I): если расположить ось буравчика вдоль оси вращения и вращать его рукоятки в направлении движения материальной точки (в направлении ее линейной скорости), то направление поступательного движения конца буравчика укажет направление вектора углаd.
Движение материальной точки (а также центра масс материального тела) по окружности характеризуется угловой скоростью ω и угловым ускорением . Как в кинематике поступательного движения, можно ввести понятие средней и мгновенной угловой скорости, углового ускорения.
Средняя угловая скорость CP равна отношению угла поворота радиус-вектора материальной точки ко времени t, за которое этот поворот произошел:
![]() ,
,
где eZ– единичный вектор оси вращенияZ.
Средняя угловая скорость CP показывает, на какой угол повернулся радиус-вектор материальной точки за единицу времени. Измеряется она в единицах рад/c, чаще, опуская наименование "радиан" используют секунду в минус первой степени (с –1).
Мгновенная угловая скорость – это угловая скорость движения материальной точки в данный момент времени, в данной точке траектории.
Мгновеннаяугловаяскоростьω– векторная физическая величина, равная первой производной угла поворота радиус-вектора материальной точки по времени:
![]()
Физический смысл мгновенной и средней угловой скорости одинаков – они характеризуют угол, на который повернулся радиус-вектор за единицу времени. Соотношения (1.12) и (1.13) указывают, что векторы угловой скорости параллельны вектору угла поворота d.
Векторы средней и мгновенной угловой скорости откладывают на оси вращения, их направление определяется по правилу (Б.I) буравчика (правого винта):
если расположить буравчик вдоль оси вращения и вращать рукоятки в направлении движения материальной точки (в направлении ее линейной скорости), то направление поступательного движения конца буравчика укажет направление вектора угловой скорости.
Среднееугловоеускорение(или)– векторная величина, равная отношению приращения угловой скоростик промежутку времени, за который это изменение произошло:
![]() .
.
Угловое ускорение показывает, на сколько изменилась угловая скорость за единицу времени.
Мгновенноеугловоеускорение(или) – векторная величина, равная первой производной угловой скоростиили второй производной углаповорота по времени:
![]()
Угловое ускорение измеряется в рад/с2, или с –2. Как следует из (1.12) и (1.13), угловое ускорение откладывают на оси вращения. При условии, что вектор совпадает по направлению с вектором угловой скоростиω, имеет место ускоренное вращение, если вектор направлен противоположно векторуω, то характер вращения – замедленный.
Основными характеристиками вращательного движения являются:
периодвращения(обращения) Т – время одного полного оборота.
частотавращения n (используют также обозначенияf, или) – число полных оборотов в единицу времени.
Период вращения Т измеряется в секундах ( [T]=c), частота вращения в с–1( [n]=c-1).
Очевидна связь частоты и периода вращения:
![]() .
.
Положив в соотношении (1.12) =2иt=T, получим для средней угловой скорости:
![]() .
.
.
.
При равнопеременном вращательном движении угол поворота , угловая скоростьи угловое ускорениесвязаны соотношениями, аналогичными соотношениям, полученным для поступательного движения. Интегрируя соотношения (1.13) и (1.15), приходим к основным уравнениям кинематики вращательного движения:

здесь 0– начальная угловая скорость.
Эти уравнения решают основную задачу кинематики для вращательного движения, если известны начальная угловая скорость 0и угловое ускорение.
Приведем важное соотношение, определяющее число Nоборотов, совершенных телом:
 ,
,
где положительный знак пишется при ускоренном вращении, знак минус – при замедленном.



