2.7. Динамика вращательного движения относительно неподвижной оси

В предыдущем разделе рассмотрено вращательное движение материальной точки. Многие понятия этого раздела легко обобщаются на случай вращательного движения твердого тела конечного размера. Вращательным движением твердого тела называют движение, при котором все точки тела описывают окружности в плоскостях, перпендикулярных оси вращения, при этом их центры лежат на оси вращения. Для кинематического описания вращательного движения достаточно определить в пространстве положение оси вращения, величину угловой скорости, углового ускорения и использовать уравнения кинематики вращательного движения.

Рассмотрим систему, состоящую из n материальных точек. На объекты системы могут действовать внутренние силы, т. е. силы, определяемые взаимодействиями объектов между собой, и внешние силы – силы со стороны тел, не входящих в систему. Для i-й материальной точки механической системы (тела) можно записать уравнение вида (2.40):

, (j=1, 2, …, n).

Запишем аналогичные уравнения для всех элементов системы и сложим их почленно:

.

Преобразуем левую часть полученного уравнения:

,

где dL/dt=dL_i/dt – момент импульса системы. Отметим, что соотношение (2.43) указывает на аддитивность момента импульса.

Используя третий закон Ньютона и аддитивность момента сил, легко показать, что суммарный момент внутренних сил равен нулю. Таким образом, двойная сумма в правой части уравнения (2.42) равна результирующему моменту внешних сил:

.

С учетом сказанного уравнение (2.42) принимает вид:

.

Это уравнение отличается от уравнения (2.29), записанного для одной материальной точки тем, что теперь L – это момент импульса системы материальных точек относительно точки. Однако, как и для отдельной точки,

• скорость изменения момента импульса механической системы равна моменту внешних сил, действующих на нее.

Если рассматривать вращение системы относительно оси Z, то уравнение (2.45) преобразуется следующим образом:

,

где L_Z момент импульса системы относительно оси вращения Z, M_Z – суммарный момент внешних сил относительно той же оси.

Твердое тело, вращающееся вокруг неподвижной оси с постоянным угловым ускорением (_z = const), можно рассматривать как механическую систему, образованную совокупностью бесконечно малых материальных точек dm. Таким образом, результаты, полученные выше для механической системы, можно использовать при описании движения твердого тела. В частности, применимо уравнение (2.37) в векторной или скалярной форме:

6. 2.7.1. Момент инерции твердого тела

Момент инерции твердого тела – величина аддитивная. Момент инерции твердого тела относительно некоторой оси равен арифметической сумме моментов инерции частиц, составляющих это тело, относительно той же оси:

,

здесь J_i – момент инерции i-ой частицы, на которые можно мысленно разбить тело. Говоря иначе, момент инерции твердого тела относительно некоторой оси равен сумме произведений элементарных масс dm_i тела на квадраты расстояний этих масс от той же оси вращения:

.

Для твердого тела, с непрерывным распределением вещества, момент инерции находят интегрированием по объему V, занятым телом:

,

где dm=dV,  – плотность тела, dV – элементарный объем.

B качестве примера вычислим момент инерции однородного диска относительно оси симметрии, перпендикулярной плоскости диска (см. рис. 2.17). Пусть толщина диска h, радиус R, плотность . Для вычислений воспользуемся полярной системой координат ,. Элементарная масса частицы диска равна dm=hrdrd, элементарный момент инерции dJ==hr³drd. Используя (2.49) запишем:

.

Произведение hR² равно массе М диска, окончательно

.

Рис. 2.17. К вычислению момента инерции диска.

Момент инерции однородного тела вращения с некоторой образующей, заданной функцией f(z), вычисляется следующим образом. Пусть твердое тело имеет плотность . Тогда (см. (2.49))

,

где L – длина тела вращения.

Таблица 2

Моменты инерции некоторых тел правильной геометрической формы

Тело	Ось, относительно которой определяется момент инерции	Формула момента инерции
Однородный тонкий стержень массой m и длиной L	Проходит через центр тяжести стержня перпендикулярно стержню	mL2/12
	Проходит через конец стержня перпендикулярно стержню	mL2/3
Тонкое кольцо, обруч, труба радиусом R и массой m, маховик радиусом R и массой m, распределенной по ободу	Проходит через центр перпендикулярно плоскости основания	mR2
Круглый однородный диск (цилиндр) радиусом R и массой m	Проходит через центр диска перпендикулярно плоскости основания	mR2/2
Однородный шар массой m и радиусом R	Проходит через центр шара	2mR2/5

Теорему Штейнера примем без доказательства:

• момент инерции тела Jотносительно оси, не проходящей через его центр масс, равен сумме двух слагаемых. Первое слагаемое равно моменту инерции телаJ₀относительно оси, проходящей через центр масс и параллельной данной. Второе слагаемое – произведение массы тела на квадрат расстоянияbмежду осями:

J = J₀+mb².

Решение задач по динамике движения материальной точки по окружности

Пример 2.4.

Определить угол между вертикальной осью конического маятника и нитью, если тело движется с постоянной угловой скоростью . Длина невесомой нити подвеса L.

Решение

=?

, L, g=9,8 м/с²

Пусть масса конического маятника равна m. Движение материальной точки происходит в горизонтальной плоскости под действием силы натяжения нити Т и силы тяжести mg (см. рисунок).

Основной закон динамики для данной задачи имеет вид:

ma = Т + mg. (1)

Выберем начало системы координат в центре движущегося по окружности тела так, чтобы ось Х проходила через центр окружности, а ось Y направим вверх. Проецируя уравнение (1) на оси, имеем:

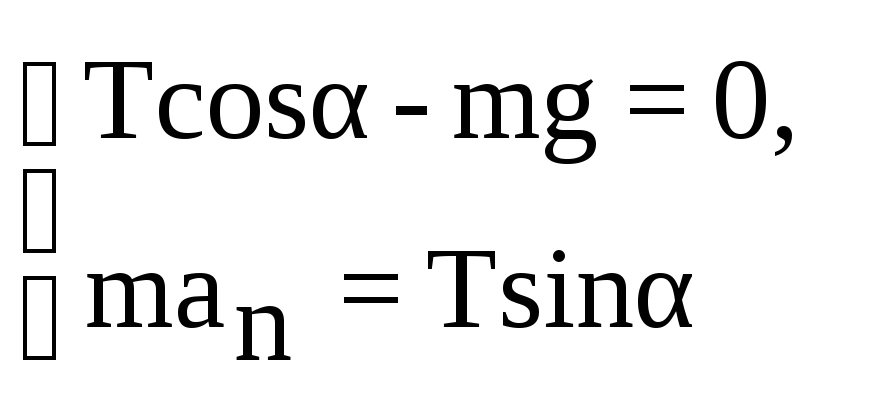(2)

Нормальное ускорение материальной точки а_n = ²r. Из чертежа следует, что радиус траектории маятника r=ОМ равен r=Lsin, где L=МВ – длина подвеса. Используя дополнительные соотношения, преобразуем уравнения системы (2):

(3)

Из уравнений (3) следует:

cos = g/²L,

или

 = arccos(g/²L).

Пример 2.5.

На веревке длиной R = 1м висит груз массой m = 5 кг. Максимальное натяжение, которое может выдержать веревка, T_MAX = 60 Н. Оборвется ли веревка, если ее отклонить на угол  = 30? На какой максимальный угол можно отклонить веревку, чтобы она не разорвалась?

MAX=? ОА=R=1м, m=5 кг, TMAX=60 H, =30

Решение.

На груз m действуют две силы: сила тяжести mg и сила натяжения Т. Основной закон динамики принимает вид:

ma = mg + Т. (1)

Выберем начало системы координат в центре движущегося по окружности тела так, чтобы ось Y проходила через центр окружности, а ось Х направим по касательной.

Проецируя уравнение (1) на оси Y и X имеем:

(2)

Ускорение а_х, входящее во второе уравнение системы (2) представляет собой тангенциальное ускорение и указывает, что модуль скорости движущегося тела меняется с течением времени. Сила натяжения Т в точке А определяется первым из уравнений (2):

(3)

Ускорение a_Y, есть нормальное или центростремительное, ускорение а_n. Очевидно, что максимальное натяжение веревка испытывает в точке А, так как в этой точке тело имеет максимальную скорость, а значит – максимальное нормальное ускорение. Используя выражение a_Y=а_n=V²/R для нормального ускорения, преобразуем уравнение (3):

(4)

Скорость тела в точке А можно определить с помощью закона сохранения механической энергии. В точке наибольшего отклонения полная механическая энергия – это потенциальная энергия е_П = mgh, где h = R(1- соs). В точке А механическая энергия равна кинетической (за нулевой уровень потенциальной энергии удобно принять уровень соответствующий нижней точке А). Уравнение закона сохранения энергии запишем так:

.

Откуда получим, что квадрат скорости с точке А равен

. (5)

Подставляя в (4) выражение (5) получим окончательно для силы натяжения:

. (6)

Подставляя в (6) максимальное значение силы Т=Т_max можно определить угол при котором веревка оборвется, т. к. достигается предельное усилие. Расчеты дают что _max=45.

Итак, если веревку отклонить на 30°, то она не оборвется.

Пример 2.6.

Тело скатывается с вершины гладкой сферической поверхности радиуса R. Найти, при какой скорости тело оторвется от поверхности. Считать, что трение отсутствует.

Решение.

H=? R =0

На скользящее тело действуют сила тяжести mg и сила N нормальной реакции полусферы. Уравнение движения имеет вид

. (1)

Направим ось Х по касательной поверхности полусферы, ось Y – радиально в направлении ее центра. Проецируя уравнение (1) на оси получим:

Преобразуем полученные уравнения.

(3)

Если учесть, что время движения dt может быть вычислено по формуле dt=dℓ/V, где dℓ=Rd, то первое уравнение приводится к следующему виду

.

Интегрируя последнее по V и , получим соотношение

. (4)

В момент отрыва тела от полусферы реакция опоры обращается в ноль, и второе из уравнений (3) принимает вид

(5)

исключив  из соотношений (4) и (5) найдем

.

Пример 2.7.

Найти максимальную разность между силами натяжения нити при вращении в вертикальной плоскости шарика массой m на невесомой нити.

Решение

(Т1-Т2)МАХ=? m

На шарик действуют две силы: сила натяжения Т и сила тяжести mg. Уравнение движения (второй закон Ньютона) запишется так:

. (1)

Для нахождения максимальной разности между силами натяжения, возникающими при вращении шарика, вычислим силы натяжение нити в точках 1 и 2.

Для положения 1 уравнение движения в проекции на оси координат "1" запишется в виде:

, (2)

где .

Аналогично, в положении 2 для проекций в системе координат "2" имеем :

. (3)

так как , то из (2) и (3) имеем

(4)

Разность определим из закона сохранения энергии. Если выбрать за нулевой уровень отсчета потенциальной энергии уровень точки 1, то можно записать, что

.

Следовательно,

. (5)

Подставляя (5) в соотношение (4) имеем окончательно

.

Пример 2.8.

Вал в виде сплошного цилиндра массой m=10 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой m₁=2 кг. С каким ускорением a будет опускаться гиря, если её предоставить самой себе.

a=?

m=10 кг, m₁=2 кг

Решение

В задаче участвуют два тела, совершающие различные движения: тело m₁ движется прямолинейно, вал – вращается. Уравнения движения имеют следующий вид:

, (1)

в системе уравнений (1) введены обозначения: а_ – тангенциальное ускорение точек на периферии вала, Т – сила натяжения шнура, r – радиус вала, М – момент, вращающий вал, а – ускорение тела m₁.

Момент, вращающий вал равен ,J – момент инерции вала относительно геометрической оси. Рассматривая вал как однородный цилиндр, считаем, что его момент инерции равен J = 1/2m₁r².

Определим направление векторных величин (по правилу буравчика) и выбрав направление осей координат как показано на рисунке запишем систему (1) в проекциях.

(2)

При условии, что шнур нерастяжим и отсутствует его скольжение по поверхности вала тангенциальное ускорение а_ по модулю равно поступательному ускорению а груза m₁: а_=а. С учетом дополнительных соотношений уравнения системы (1) примут вид:

(3) Решая систему относительно ускорения a получим:

.

Пример 11.

Через блок в виде диска, имеющий массу m=80г, перекинута тонкая гибкая нить, к концам которой подвешены грузы массами m₁=100г и m₂=200г. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением пренебречь.

Решение.

а1, а2=? m=80 г=810–2 кг m1=100 г =10–1 кг m2=200 г=210–1 кг

Рассматриваемая в задаче система состоит из двух движущихся поступательно грузов и одного вращающегося диска. На каждый из грузов действует две силы: сила тяжести mg, направленная вниз, и силаТнатяжения нити, направленная вверх. Запишем законы поступательного и вращательного движения этих тел.

(1)

Результирующий вращающий момент, приложенный к диску, равен

М=М₂+М₄=[R₁,T₂]+[R₂,T₄],

R₁иR₂– радиус-векторы точек приложения сил натяжения нитиT₂иT₄. Предположим, чтоm₂>m₁, поэтому ускорения грузов будет направлено, как показано на рисунке. Выберем произвольное направление осей координат (например, как на рисунке) и запишем систему уравнений в проекциях.

(2)

При условии, что нить нерастяжима, отсутствует ее скольжение по поверхности диска, тангенциальное ускорение точек на поверхности диска а_по модулю равно поступательному ускорениюагрузов: а_=а. Угловое ускорение диска связано с линейным ускорением грузов соотношением; в скалярной форме. Пренебрегая массой нити приходим к выводу, что силы натяжения Т₁и Т₂равны по величине. Учтем также, что момент инерции дискаJ=mr²/2. С учетом приведенных дополнительных соотношений система (2) принимает вид:

Решая полученную систему, получим

.

После подстановки числовых значений имеем