Лекционный блок
Глава 1. Кинематика
1.1. Основные понятия
Механика – раздел физики, изучающий закономерности механического движения тел и причины, вызывающие (или изменяющие) его.
Механическое движение – процесс изменения с течением времени взаимного расположения тел или частей тела относительно друг друга.
Кинематика – раздел физики, изучающий механическое движение тел, безотносительно к причинам, вызывающим это движение.
Классическая (нерелятивистская ) механика или механика Ньютона – нерелятивистская теория движения макроскопических объектов.
Нерелятивистская теория –теория движения тел со скоростями V, гораздо меньшими скорости света с: V<<с.
Основная задача кинематики (механики) состоит в определении положения и скорости движущейся материальной точки (тела) в произвольный момент времени.
Материальная точка – модель реального тела:
размеры которого стремятся к нулю, говорят: материальная точка не имеет размеров,
имеет не равную нулю массу.
В конкретной задаче материальной точкой можно считать тело, размеры которого много меньше, чем расстояния между телами, или размеров области, в которой происходит движение.
Абсолютно твердое тело – тело, расстояние между любыми точками которого всегда остается неизменным. Такое тело не способно деформироваться, но под действием внешних сил в нем могут возникать внутренние напряжения, силы упругости и давления.
Поступательным движением называют движение, при котором любая прямая, проведенная в теле остается параллельной сама себе.
Для указания положения материальной точки в пространстве и описания изменения этого положения во времени вводят систему отсчета.
Система отсчета – совокупность: 1) тела отсчета (тела, по отношению к которому определяется положение некоторой материальной точки); 2) системы координат с началом отсчета в точке, выбранной на теле отсчета, 3) часов – прибора для отсчета времени. Можно говорить, что система отсчета представляет собой систему координат, жестко связанную с телом отсчета и часы.
Радиус-вектор r материальной точки – это вектор, проведенный из начала координат системы отсчета к этой материальной точке.
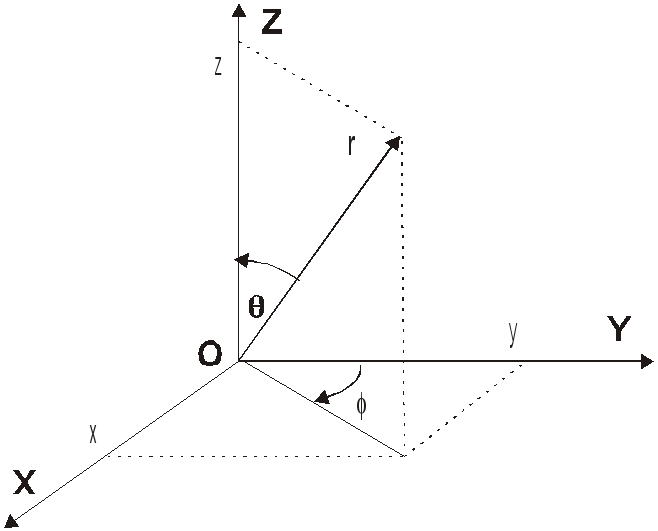
Наиболее часто при решении задач на плоскости вводят декартовы прямоугольные координаты (x, y) и полярные координаты (r, φ); в трехмерном пространстве – декартовы прямоугольные (x, y, z), цилиндрические (z, r, φ) и сферические (r, Θ, φ) системы координат. В декартовой системе координат координаты (x, y, z) материальной точки М определяют как проекции радиус-вектора r этой точки на соответствующие оси системы координат. Взаимосвязь названных систем координат иллюстрируют приведенные ниже рисунки.
|
|
Рис.1.1а. Декартовы x,y и и полярные r, , координаты
|
|
|
Рис.1.1b. Соответствие декартовых x,y,z и и цилиндрических r, , z координат
|
|
|
Рис.1.1с. Соответствие декартовых x,y,z и сферических r, , координат
|
Движение материальной точки в пространстве сопровождается изменением ее координат (и ее радиус-вектора) с течением времени. Процесс движения может быть описан системой уравнений, представляющей собой параметрическое уравнение траектории:
или уравнением для радиус-вектора:
,
где радиус вектор r=(x,y,z).
Траектория материальной точки может быть определена следующими способами:
линия, вдоль которой движется материальная точка (центр масс материального тела) в данной системе отсчета,
геометрическое место концов радиус-векторов материальной точки.
Уравнение траектории в явном виде, как уравнение, связывающее между собой пространственные координаты движущейся материальной точки, может быть получено исключением времени из системы уравнений (1.1).
Путь (длина пути) – скалярная величина численно равная длине участка траектории, пройденного материальной точкой от начального положения С до конечного В (см. рис. 1.2).
|
|
Рис. 1.2. АСВ - траектория движения материальной точки, r0 и r – ее начальный и конечный радиус-векторы, r=S – вектор перемещения |
Перемещение – вектор S направленный из начального положения движущейся материальной точки в ее конечное положение.
Вектор перемещения S можно определить как приращение r радиус-вектора материальной точки: S=r = r1 – r0. Рисунок 1.2 позволяет сделать вывод, что модуль вектора перемещения совпадает с длиной пройденного пути лишь при прямолинейном движении.