
- •Тема 1: Формулы комбинаторики и вероятность, аксиомы Колмогорова. Алгебра событий. Классическое определение вероятности.
- •Основные понятия.
- •Классическое определение вероятности.
- •Напомним, что числа a и есть количество элементов во множествах a и соответственно.
- •3.Свойства вероятности.
- •4.Относительная частота. Статистическое определение вероятности.
- •5. Формулы комбинаторики.
- •6. Применение формул комбинаторики при решении задач по теории вероятности.
- •7. Общие определения вероятности. Аксиомы а.Н. Колмогорова. Алгебра событий.
- •Аксиомы, задающие вероятность.
- •Тема 2: Условная вероятность. Независимые события. Формула полной вероятности и Байеса.
- •1. Условная вероятность. Независимые события.
- •2. Формула полной вероятности и Байеса.
- •Тема 3: Схема Бернулли. Формулы Муавра-Лапласа. Функция Лапласа и ее свойства.
- •1. Последовательность независимых испытаний.
- •В данном случае ,,. Вычислим;. Поэтому. Так как, то. Следовательно, наиболее вероятное число выпаданий шестерки равно 3.
- •2. Приближенные формулы для Pn(k) при больших значениях n и k.
- •Тема 4: Случайные величины. Непрерывные и дискретные случайные величины. Закон распределения случайных дискретных величин. Бином распределения, распределение Пуассона.
- •1. Определение случайной величины.
- •2. Дискретные случайные величины.
- •3. Характеристики случайных величин.
- •4. Примеры дискретных случайных величин.
- •Тема 6: Функция распределения случайной величины. Нормально распределенные случайные величины.
- •Примеры непрерывных случайных величин. Равномерное распределение на отрезке.
- •Тема 5: Числовые характеристики случайных дискретных величин: математическое ожидание, дисперсия, среднеквадратичное отклонение.
- •1. Математическое ожидание и дисперсия.
- •2. Нормированные случайные величины.
- •1.Определение характеристик случайных величин на основе опытных данных.
Тема 3: Схема Бернулли. Формулы Муавра-Лапласа. Функция Лапласа и ее свойства.
В этом параграфе мы рассмотрим одну стандартную ситуацию, которая может возникнуть при решении практических задач.
1. Последовательность независимых испытаний.
Пусть A
есть некоторое случайное событие по
отношению к некоторому опыту σ.
Обозначим
![]() ;
;![]() ,
где
,
где![]() .
В качестве примера рассмотрим опыт,
состоящий в бросании игрального кубика,
а в качествеA
возьмем
случайное событие, состоящее в выпадении
6и
очков. Очевидно, что в этом примере
.
В качестве примера рассмотрим опыт,
состоящий в бросании игрального кубика,
а в качествеA
возьмем
случайное событие, состоящее в выпадении
6и
очков. Очевидно, что в этом примере
![]() ;
;![]() .
.
Пусть опыт σ повторяется независимо n раз. В каждом испытании событие A может как наступить, так и не наступить. Обозначим через Pn(k) вероятность того, что при n независимых испытаниях событие A произойдет k раз, где k ≤ n.
Теорема (Бернулли). Имеет место формула.
![]() .
(1)
.
(1)
Определение. Формула (1) называется формулой Бернулли, а многократное повторение опыта σ, при каждом из которых может наступить с одной и той же вероятностью событие A называется схемой Бернулли.
Задача. Доказать формулу (1).
Пример. Вернемся к первому примеру. Пусть игральный кубик бросается 3 раза. Найти вероятность того, что шестерка выпадет 2 раза.
Ответ дается
формулой (1), в которой
![]() ,
,![]() ,
,![]() ,
,![]() :
:
 .
.
Приведем еще две формулы, применяемые в задачах, связанных со схемой Бернулли.
Вероятность не наступления события A в течение n испытаний согласно формуле Бернулли равна
![]() .
.
Пусть B
есть событие, состоящее в том, что в n
опытах событие A
ни разу не произойдет. Пусть C
есть случайное событие, состоящее в
том, что в n
опытах событие A
произойдет хотя бы один раз. Очевидно,
что B
и C
образуют полную группу событий. Поэтому
![]() .
.
По доказанному
![]() .
.
Следовательно,
![]() .
.
Определение. Число k = k0, при котором вероятность Pn(k) является наибольшей, называется наивероятнейшим числом наступления события A в n испытаниях.
Теорема. Если
![]() и
и![]() ,
то числоk0
удовлетворяет
двойному неравенству
,
то числоk0
удовлетворяет
двойному неравенству
![]() .
(2)
.
(2)
Замечание.
Если
![]() ,
то имеются два наивероятнейших значения
,
то имеются два наивероятнейших значения![]() и
и![]() .
.
Пример. Игральный кубик бросается 20 раз. Каково наиболее вероятное число выпадений 6и очков.
Решение.
В данном случае ,,. Вычислим;. Поэтому. Так как, то. Следовательно, наиболее вероятное число выпаданий шестерки равно 3.
Замечание. Из последней теоремы следует, что одно из двух целых чисел (а иногда оба), ближайших к числу np, являются наиболее вероятным числом успехов. Число np допускает и другую важную интерпретацию. А именно, np можно рассматривать в определенном смысле как среднее число наступлений события A в n опытах. Этот факт точно формулируется и строго обосновывается в предельных теоремах теории вероятности.
2. Приближенные формулы для Pn(k) при больших значениях n и k.
Часто при решении задач приходится вычислять вероятности Pn(k) при больших значениях n и k, при которых вычисления по формуле Бернулли (1) сложно и громоздко. В этом случае используют приближенные формулы Муавра-Лапласса для случая, когда оба числа p и q не являются малыми. Приведем эти формулы.
Если n велико, то из локальной теоремы Муавра-Лапласса следует приближенная формула
 ,
,
![]() ,(3)
,(3)
где
 .
.
В конце пособия приведена таблица значений функции φ(x). Заметим, что φ(x) – четная функция, то есть φ(-x) = φ(x). Поэтому в таблице приводятся значения φ (x) только для положительных значений аргумента.
При больших n вероятности Pn(k) близки к 0. Поэтому на практике вычисляют вероятность попадания числа успехов в заданный промежуток.
Пусть k
есть число наступлений события A
в n
опытах. Обозначим через Pn(k1,k2)
вероятность того, что
![]() .
.
Если n велико, то из интегральной теоремы Муавра-Лапласса следует приближенная формула
![]() ,
(4)
,
(4)
где
![]() ,
,![]() ,
(5)
,
(5)
а
![]() есть функция Лапласса:
есть функция Лапласса:
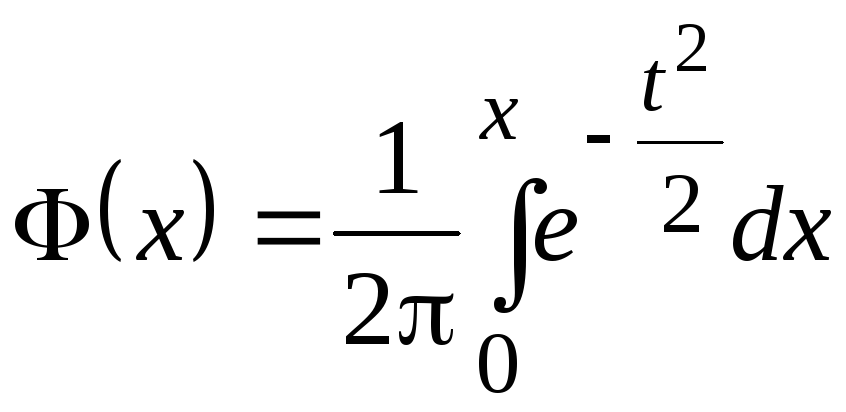 .
(6)
.
(6)
Таблица значений функции Ф приведена в конце пособия.
Перечислим без доказательства известные свойства функции Ф(x):
Ф(x) – нечетная функция.
Ф(x) – возрастает.
 ,
,
 .
.
График функции y = Ф(x) изображен на рисунке

Пример.
Вероятность поражения мишени стрелком
равна
![]() .
Какова вероятность того, что при 300
выстрелах мишень будет поражена.
.
Какова вероятность того, что при 300
выстрелах мишень будет поражена.
а) ровно 72 раз; б) от 66 до 84 раз?
Решение.
В этом примере n = 300, p = 1.25, q = 1 – 0.25 = 1.75, k = 72. В соответствии с формулами (3) вычисляем
![]() ;
;
По таблице значений φ (x) находим значение φ (–0,4) = φ (0.4) = 0.368. Тогда по формуле (3)
![]()
Далее по условию k1 = 66, k2 = 84. По формулам (5) вычислим
![]() ,
,
![]() .
.
![]()
Значение функции
![]() найдено по таблице.
найдено по таблице.
Замечание. Если одно из чисел p или q близко к 0, то значения Pn(k), вычисленные по приближенным формулам, сильно отличаются от точных значений. В этом случае рекомендуется использовать приближенную формулу Пуассона. Приведем эту формулу.
Пусть вероятность p мала. Тогда
![]() ,
где
,
где
![]() .
.
