Контрольные вопросы:

1. Декартово произведение двух и более множеств.

2. Свойства декартова произведения множеств.

3. Графическое изображение декартова произведения двух числовых мно­жеств.

4. Число элементов в декартовом произведении конечных множеств.

5. Связь введенных понятий с начальным курсом математики.

Литература: (1) гл. I, § 1 п. 6; (2) гл. I, § 1, с. 25-33, 38-39; (3) гл. I, § 1 п.5; (4) гл. I, с. 37-38; (5) гл. I, §§ 1.4, 1.7.

Введем, прежде всего, понятие пары. Это понятие часто встречается в обыденной жизни: пара рукавиц, пара глаз, пара детей и т.д.

В школьном курсе математики с парами встречаемся в процессе знакомства с прямоугольной системой координат. Обыкновенная дробь – это тоже пара двух чисел.

В общем случае под парой будем понимать два элемента, расположенных в определенном порядке (в этом случае говорят об упорядоченной паре элементов). Символическая запись: (а; b) или <а; b>. Если дана пара (а; b), то а – это первая компонента пары, а b – вторая компонента пары.

Определение: Две пары и назовем равными, если их соответствующие компоненты равны, т.е. и ; назовем различными, если хотя бы одна из компонент первой пары не равна соответствующей компоненте другой пары, т.е. или .

Обобщением понятия пары является «тройка», «четверка», и т.д. «п-ка» элементов.

Всякую упорядоченную систему (набор) элементов назовем кортежем. Например, запишем множество букв в слове «параллелограмм»: А= {п; а; р; л; е; о; г; м} и кортеж букв в этом слове: <п; а; р; а; л; л; е; л; о; г; р; а; м; м>.

Замечание: В кортеже в отличие от множеств существенен порядок следования элементов, а также допускается выписывание одинаковых элементов.

Пусть даны два непустых множества А и В и пусть а.

Определение: Декартовым произведением двух непустых множеств А и В называется множество упорядоченных пар (а; b) таких, что а.

Символическая запись: .

= {(а; b)| а}.

Операция отыскания декартового произведения двух множеств называется декартовым умножением.

Если хотя бы одно из множеств А или В является пустым множеством, то естественно принять, что и их декартово произведение - пустое множество.

Пусть А= Ø, а В Ø. Тогда = {(а; b)| а Ø, bВ }.

а Ø – это ложное утверждение, т.к. пустое множество элементов не содержит. Следовательно, пары (a; b) не существует, т.к. не существует элемента а. Тогда Ø В= Ø. Аналогично, А Ø= Ø, и Ø Ø = Ø.

Пример: Пусть А= {x; y}, В = {1; 2; 3}. Тогда = {(x; 1), (x; 2), (x; 3), (y; 1), (y; 2), (y; 3)}. Заметим, что декартово произведение , в этом случае, задано перечислением элементов.

Замечание: Если множества А и В равны (А=В), то = и называется декартовым квадратом.

Определение: Декартовым произведением «п» множеств называется множество упорядоченных «п-ок» таких, что

Из данного определения следует, что декартово произведение двух множеств – это частный случай декартова произведения «п» множеств.

Если , то

Способы задания декартова произведения двух множеств

По определению декартово произведение двух множеств – это множество, значит, оно так же задается: 1) перечислением элементов и 2) указанием характеристических свойств.

Перечислением элементов декартово произведение задано в рассмотренном ранее примере, где А= {x; y}, В= {1; 2; 3} и = {(x; 1), (x; 2), (x; 3), (y; 1), (y; 2), (y; 3)}.

Запись декартового произведения на математическом языке – это и есть его задание на языке характеристических свойств: = {(а; b)| а}.

Если множества А и В – конечные множества, то и их декартово произведение так же конечное множество. Перечислить элементы множества можно по-разному, например, с помощью таблицы, графа. Зададим = {(x; 1), (x; 2), (x; 3), (y; 1), (y; 2), (y; 3)} с помощью таблицы:

A B	1	2	3
x	(x;1)	(x;2)	(x;3)
y	(y;1)	(y;2)	(y;3)

С помощью графа:

x

y

1

2

3

Если множества А и В – числовые, то их декартово произведение можно изобразить на координатной плоскости. В этом случае говорят о графическом задании декартова произведения множеств. Декартово произведение множеств А= {x; y} и В= {1; 2; 3} задать графически нельзя, т.к. А не является числовым множеством.

Пусть A = {x| xR, x3}= (-;3], а B = {y| yR, |y|5}= [-5;5].

З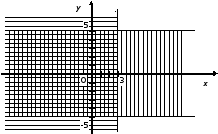ададим декартово произведение этих множеств на координатной плоскости. Изобразим множествоА по оси (Ox), а множество В по оси (Oy). Множество точек координатной плоскости, абсцисса которых есть действительное число, меньшее или равное 3 (x3) располагается левее прямой x = 3 (горизонтальная штриховка). Множество точек, ордината которых есть действительное число, модуль которого меньше или равен 5, располагается между прямыми y = -5 и y = 5 (вертикальная штриховка). Тогда декартово произведение множеств А и В – это множество точек, расположенных левее прямой x = 3 и между прямыми y = -5 и y = 5. (двойная штриховка).