Отображения

Пусть F-соответствие между элементами множеств Х иY: F = <X ,Y,G_F >, где

G_F ХY и G_F ={ (x,y)/x X, y Y, x F y}.

Определение: Отображением множества Х во множество Y называется такое соответствие F между элементами множеств X и Y, при котором каждому элементу множества Х соответствует один и только один элемент множества Y.

Иначе говоря: отображение множества Х во множество Y - это такое соответствие между элементами множества Х и Y, при котором полный образ элемента хХ есть одноэлементное множество.

Из определения отображения следует, что отображение F- это частный случай соответствия между элементами множеств Х и Y. Естественно, что у него есть свои особенности.

Особенности, присущие отображению:

1) область определения отображения совпадает с областью отправления: т.е. D_F =X;

2) полный образ любого элемента аХ - есть одноэлементное множество: аХF(a) - одноэлементное множество;

3) полный прообраз некоторых элементов bY может быть пустым: b YF^-1 (b)- может быть пустым;

4) F(X) – назовем полным образом множества Х ;

5) особенности графика: графику отображения множества Х во множество Y не могут принадлежать пары (x,y) с одинаковыми первыми и различными вторыми компонентами;

6) особенности графа отображения множества Х во множество Y: из каждой точки множества Х выходит только одна стрелка;

7) особенности обозначения: х ^f y ( f: < X, Y, G_f >). Соответствия такого вида (отображения) принято обозначать буквой f. (Можно писать: f = < X,Y,G_f > или

y = f(x), xX).

Пример 1. Является ли данное

X Y соответствие

отображением?

f₁

1 = f₁(a)

1 = f₁(b).

1 = f₁(c)

Очевидно, что каждый элемент из множества Х имеет единственный образ. Следовательно f₁ – отображение множества X во множество Y.

Видим, что Д=X, E = {1}, F(X) = {1}.

X Y

Пример 2. f₂

Cоответствие f₂- не является отображением, так как, например, f₂ (b) = Ǿ ( и не только), кроме того f₂(a)={1; 2}, т.е. элемент аимеет два образа.

Виды отображений

Пусть f = <X,Y,G_f >, где G_f - это отображение множества X во Y.

Определение: Отображение f = <X,Y,G_f >, где G_f , при котором каждый элемент уY, имеет хотя бы один прообраз хХ, называется сюрьективным ( или сюрьекцией)

Иначе говоря: при сюрьективном отображении полный образ множества X совпадает с областью прибытия Y: f(X) = Y и полный прообраз каждого уY- непустое множество.

Особенности графа сюрьективного отображения: к каждому уY подходит хотя бы одна стрелка.

В примере 1 отображение не является сюрьекцией , т.к 2Y не имеет прообраза.

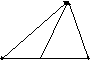
Пример 3. X = [АВ ] - отрезок АВ.

Y = {O} - точка О. Соответствие f₃ задано графом:

О А0

В0

М0 М[AB]

А М В

Является ли f₃-отображением? Является, т.к каждой точке отрезка АВ соответствует только одна точка (т. О). Кроме того, оно является сюръективным.

Замечание: если f –множества X воY сюрьективно, то говорят об отображении множества X на Y.

Определение: Если каждый элемент уY является образом не более одного элемента хХ , то отображение f называется иньективным (иньекцией).

Иначе говоря: при инъективном отображении полный образ множества X есть подмножество области прибытия Y и полный прообраз каждого уY состоит не более, чем из одного элемента хХ.

Определение:отображение Х ^f Y называется биективным (биекцией), если оно сюрьективно и иньективно.

Иначе говоря: при биективном отображении полный образ множества X совпадает с областью прибытия и прообраз каждого элемента уY состоит только из одного элемента хХ.

Замечание1 : Биективное отображение множества Х на множество Y- это взаимно-однозначное соответствие между элементами этих множеств.

Замечание 2 :Синонимом понятия отображения множества Х во Y является понятие функция. Вместо отображения иначе говорят: функциональное соответствие.