Импликация высказываний

Пусть даны высказывания А и В .

Определение: Импликацией высказываний А и ,В назовём высказывание

«если А, … то В» (), которое ложно тогда и только тогда, когда А – истинно, В – ложно.

Операцию отыскания импликаций двух высказываний также называют импликацией.

Предложение «если А, ...., то В» можно читать иначе: А импликация В.

Таблица истинности импликации

высказываний

А	В
и л и л	л и и л	л и и и

Пусть дана . Тогда А – это условие данной импликации, а В – заключение. Иногда условие называют посылкой.

(1) – назовем прямой импликацией;

(2) – обратная к (1) импликация;

(3) – противоположная к прямой импликация. (Читаем: если не А, то не В);

(4) – противоположная к обратной импликация (или обратная к противоположной).(Читаем: если не В, то не А).

Закон контрапозиции

Импликация и импликация имеют одно и тоже значение истинности, т. е. они одновременно истинны или одновременно ложны:

.

Докажем с помощью таблицы истинности.

А	В
и и л л	и л и л	и л и и	л и л и	л л и и	и л и и

Задание: Докажите следующее утверждение самостоятельно:

Эквиваленция двух высказываний

Эквиваленция двух высказываний образуется при помощи логической связки: «тогда и только тогда», «если и только, если».

Определение: Эквиваленцией высказываний А и В называется высказывание которое истинно только тогда, когда высказывания А и В имеют одно и то же значение истинности, т. е. одновременно истинны или одновременно ложны.

–эквиваленция высказываний А и В. Читается «А тогда и только тогда, когда В».

Таблица истинности эквиваленции

высказываний

А	В
и и л л	и л и л	и л л и

Другое определение эквиваленции двух высказываний:

(5)

Определение:

Эквиваленция высказываний А и В – это конъюнкция прямой и обратной импликаций высказываний А и В.

Докажем утверждение (5): .

Определение: Составные высказывания, истинные при любых значениях истинности входящих в них элементарных высказываний, принято называть тавтологиями.

Задание: 1) покажите, что высказывания, данные на стр. 68 (учебника) являются тавтологиями.

2) привести примеры других тавтологий.

Законы операций над высказываниями.

1) закон двойного отрицания (доказан ранее);

2) 2.1 коммутативность конъюнкции,

2.2 дизъюнкции;

3) 3.1 ассоциативность конъюнкции и

3.2 дизъюнкции;

4.1 закон дистрибутивности конъюнкции

относительно дизъюнкции;

4.2 дизъюнкции относительно конъюнкции;

5.1 законы идемпотентности;

5.2

6) (абсолютно истинно) закон исключённого третьего

7) (абсолютно ложно) закон противоречия

8.1 законы де Моргана;

8.2

9) законы поглощения;

10) законы исключения импликации;

11)

12) закон исключения эквиваленции.

Все законы можно доказать с помощью таблицы истинности.

Второй способ доказательства путём преобразования выражений с помощью уже известных формул.

Докажем 8.2. : с помощью таблицы истинности.

А	В
и и л л	и л и л	и и и л	л л л и	л и л и	л л и и	л л л и

Сделаем некоторые замечания:

1. Если высказывание составное, то его структура выражается конечной последованию букв А_1, А₂, А₃, … А_к, обозначающих элементарные высказывания, знаков операций, выполненных над элементарными высказываниями и скобок, определяющих порядок операций.

2. Условились считать, что сильнее всех связывает знак отрицания, за ним конъюнкция, дизъюнкция и импликация. Слабее всех связывает знак эквиваленции. Название высказывания определяется по последней операции. Например, – это импликация.

3. Конечная последовательность букв, знаков логических операций и скобок, выражающая логическую структуру высказывания, называется формулой логики высказывания.

4. Для выявления логической структуры высказывания надо:

а) выделить в нём все элементарные высказывания и обозначить их буквами;

б) логические связки заменить соответствующими им символами;

в) записать с помощью букв, знаков операций и скобок логическую структуру исходного высказывания.

Высказывательные формы (предикаты).

Определение: Предложение с одной или несколькими переменными, которое обращается в высказывание при подстановке вместо переменных их значений, называется высказывательной формой или предикатом.

В зависимости от числа переменных предикаты бывают одноместными, двухместными и т.д. n –местные.

Обозначаются: А(х) – одноместный

В(х,y) – двухместный и т.д.

…

D(x_1, x_2, x_3, … х_n)

С каждым предикатом связывают три множества:

1) область определения предиката: D_{A(x) –} это множество значений переменной, при которых предикат обращается в высказывание.

2) множество истинности предиката Т_А(х) – это множество тех значений переменных из области определения предиката, при котором предикат обращается в истинное высказывание.

3) множество ложности предиката: - это множество тех значений переменной, при котором предикат обращается в ложное высказывание.

Между этими множествами существует вполне определённая связь:

Множества истинности и множества ложности предиката дополняют друг друга до области определения предиката.

Пример 1. На множестве R задано предложение Х² – 1 = 0. Является ли оно предикатом? Какова область определения? Множество истинности?

1. Х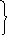² – 1 = 0 – это предложение с переменной.

1. при Х = 1, 1² – 1 = 0 – это предложение обращается в

высказывание.

это одноместный предикат: А(х): Х² – 1 = 0

D_A =R.

Т_А =

Видим, что все отношения выполняются: .

Пример 2: Дано предложение: при x = -1 выполняется равенство x + 1 = 0.

1. – это предложение с переменной, но оно является истинным высказыванием, а не предикатом.

Пример 3: С(х,у): x + y = 7,

1. предложение с двумя переменными х и y

1. обращается в высказывание, например, при x = 3 y = 5

С(3,5): 3 + 5 = 7 – высказывание (не важно сейчас какое).

D_c – это множество пар действительных чисел:

D_с =

, т.е. множество таких пар действительных чисел, для которых верно: x + y = 7.

Если подставлять значение только одной переменной, то предикат станет одноместным предикатом.

Пусть x = 10 тогда - это одноместный предикат.