
- •Математика
- •Пересечение множеств
- •Вычитание множеств
- •Свойства операций над множествами
- •Число элементов в объединении конечных множеств и в дополнении к подмножеству
- •Контрольные вопросы:
- •Способы задания декартова произведения двух множеств
- •Основные свойства декартова произведения.
- •Раздел II. Элементы комбинаторики
- •Контрольные вопросы:
- •Контрольные вопросы:
- •Перестановки без повторений
- •Бином Ньютона
- •Свойства сочетаний. Треугольник Паскаля.
- •1. Правило симметрии:
- •Раздел III. Математические утверждения и их структура
- •Контрольные вопросы:
- •Отношения между понятиями
- •Способы определения понятий
- •Требования к определению понятий
- •Контрольные вопросы:
- •Высказывания и операции над ними
- •Операции над высказываниями
- •Отрицание высказываний
- •Законы отрицания:
- •Конъюнкция двух высказываний
- •Импликация высказываний
- •Закон контрапозиции
- •Эквиваленция двух высказываний
- •Обращение предиката в высказывание
- •Операции над предикатами
- •Отрицание высказываний, содержащих кванторы
- •Отношение логического следования и равносильности на множестве предложений
- •Строение теоремы. Виды теорем
- •Закон контрапозиции. Теоремы
- •Умозаключения. Анализ рассуждений. Простейшие правила вывода
- •Простейшие схемы дедуктивных умозаключений
- •Способы установления истинности умозаключения
- •Индуктивные умозаключения
- •Раздел IV. Соответствия
- •Контрольные вопросы:
- •Полный образ и полный прообраз
- •Способы задания соответствий
- •Типы соответствий
- •Отображения
- •Виды отображений
- •Отношения
- •Свойства отношений на множестве
Операции над высказываниями
Основой для выполнения операций над высказываниями являются логические связки.
Логические связки – это союзы: «и»; «или»; «если…, то»; частица «не»; слова «неверно, что»; «тогда и только тогда,…когда»; «если и только если,…если»; «либо, либо».
С помощью этих слов из высказываний строятся другие высказывания, а процедура эта называется операцией над высказыванием.
Отрицание высказываний
Определение: Отрицанием высказывания А называется высказывание «не А» (неверно, что А), которое истинно, если А - ложно и ложно, если А – истинно.
Операцию построения отрицания высказывания также называют отрицанием высказывания. Определение можно оформить с помощью таблицы истинности:
|
|
|
|
|
и |
л |
|
|
л |
и |
|

При построении отрицания А с помощью словосочетания «неверно, что» это словосочетание ставится перед всем предложением, частица «не» ставится перед сказуемым.
Например, А: 5 – 12 = 10 – ложное высказывание;
![]() :
Неверно, что 5 – 12 = 10 или 5 - 12 не
равно
10: (5-12 ≠ 10).
:
Неверно, что 5 – 12 = 10 или 5 - 12 не
равно
10: (5-12 ≠ 10).
В: Дети нашли три жёлудя – истинное высказывание;
![]() :
Дети не нашли три жёлудя (отрицание
высказывания В)
– ложное высказывание
:
Дети не нашли три жёлудя (отрицание
высказывания В)
– ложное высказывание
![]() -
Неверно,
что дети нашли три жёлудя. – ложное
высказывание.
-
Неверно,
что дети нашли три жёлудя. – ложное
высказывание.
Законы отрицания:
Пусть
дано высказывание
![]() – отрицание высказывания А,
– отрицание высказывания А,
![]() – отрицание отрицания А
или двойное отрицание.
– отрицание отрицания А
или двойное отрицание.
Закон
двойного отрицания:
![]() .
.
Докажем его:
-



и
л
и
л
и
л
Очевидно,
что А
и
![]() одновременно истинны или ложны.
одновременно истинны или ложны.![]() А
и
А
и
![]() равносильны:
равносильны:
![]() Например, пусть
А:
5 – 12 = 10. Тогда
Например, пусть
А:
5 – 12 = 10. Тогда
![]() :
5 – 12 ≠ 10.
:
5 – 12 ≠ 10.
![]() :
5 – 12 = 10. или
:
5 – 12 = 10. или
![]() :
неверно, что 5 – 12 ≠ 10. Откуда
:
неверно, что 5 – 12 ≠ 10. Откуда
![]() .
.
Конъюнкция двух высказываний
Определение: Конъюнкцией двух высказываний А,В, называется высказывание
А
и
В
![]() ,
которое истинно
в том и только в том случае,
когда оба
высказывания одновременно истинны.
,
которое истинно
в том и только в том случае,
когда оба
высказывания одновременно истинны.
Операцию построения конъюнкции двух высказываний также называют конъюнкцией.
Строится
конъюнкция с помощью логической связки
«и», обозначается:
![]() .
И тогда высказывание «А и В» имеет вид:
.
И тогда высказывание «А и В» имеет вид:
![]() .
.
Таблица истинности конъюнкции
высказываний
|
А |
В |
|
|
и и л л |
и л и л |
и л л л |
Пусть даны высказывания: А: 5 – 12 = 10 – ложное высказывание:
В: Киев – столица Украины - истинное высказывание;
![]() :
(5 – 12 = 10) и
Киев – столица Украины - ложное
высказывание, т.к. одно из высказываний
ложно, а второе истинно.
:
(5 – 12 = 10) и
Киев – столица Украины - ложное
высказывание, т.к. одно из высказываний
ложно, а второе истинно.
Замечание: В математической логике смысл предложения не является важным, главным является структура предложения.
А: 5 – 12 = - 7 – истинное высказывание;
В: Киев – столица Украины – истинное высказывание.
![]() :
( 5-12 = -7) и
Киев – столица Украины – истинное
высказывание, т.к. оба высказывания
истинны.
:
( 5-12 = -7) и
Киев – столица Украины – истинное
высказывание, т.к. оба высказывания
истинны.
Определение: Дизъюнкцией двух высказываний А, В называется высказывание
А
или
В
(![]() ),
которое ложно
тогда и только тогда,
когда одновременно
ложны
оба высказывания А
и В.
),
которое ложно
тогда и только тогда,
когда одновременно
ложны
оба высказывания А
и В.
Операция построения дизъюнкции высказываний также называется дизъюнкцией.
Пример:
![]() :
(5 - 12 = 10) или Киев – столица
Украины. – истинное высказывание, т.к.
только одно из высказываний ложно.
:
(5 - 12 = 10) или Киев – столица
Украины. – истинное высказывание, т.к.
только одно из высказываний ложно.
Таблица истинности дизъюнкции
высказываний
-
А
В

и
и
л
л
и
л
и
л
и
и
и
л
Определение: Высказывание, которое ложно при любых значениях истинности, входящих в него элементарных высказываний называется абсолютно ложным и такое высказывание будем обозначать большой буквой Л.
Например:
![]() = Л
–
абсолютно ложное высказывание.
= Л
–
абсолютно ложное высказывание.
Определение: Высказывание, которое истинно при любых значениях входящих в него элементарных высказываний, называется абсолютно истинным. (И)
Пример:
![]() = И
– абсолютно истинное высказывание.
= И
– абсолютно истинное высказывание.
Наши рассуждения можно представить в виде таблицы истинности:
-



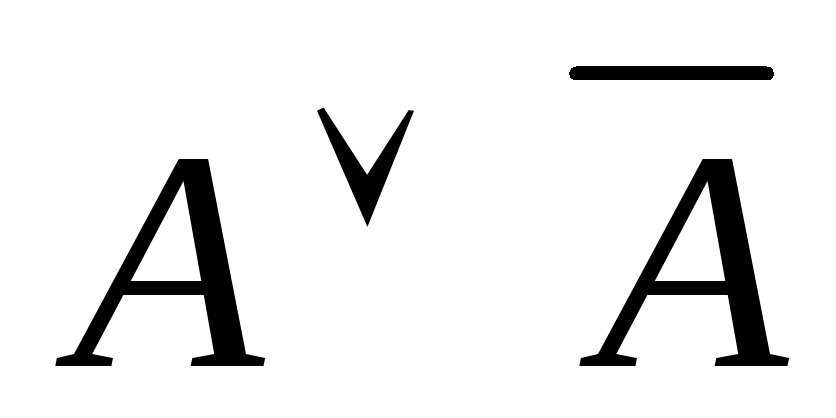
и
л
Л
И
л
и
Л
И
Задание
на дом: Выяснить, является ли высказывание
абсолютно истинным:
![]()
![]() .
.
