2. Интегральное представление классов

Важную роль в изучении классов играет интегральное представление функций из этих классов.

Сначала докажем следующее утверждение:

Теорема 3. Пусть где– класс Соболева в. Если при этом существует такое число, чтоипри, то при всехсправедливо представление

(2.5)

где, как обычно,

Доказательство. Пусть фиксировано, положим

Тогда, записав формулу Коши-Грина для функции , имеем:

Используя условие теоремы, получаем:

Упростим подынтегральное выражение:

Следовательно, из равенства (5) имеем:

Положив , получаем:

□

Из теоремы 3 непосредственно следует:

Теорема 4. Пусть . Тогда еслиилито справедливо представление

(6)

Доказательство непосредственно следует из теоремы 2.3, если учесть, что , при этом в условиях теоремы 2.4при.

□

Из интегрального представления классов вытекает:

Теорема 5. Пространство приотносительно нормы

является банаховым, а при – квазибанаховым пространством.

Доказательство. Пусть . Обозначим черезпространство измеримых в функций , для которых соответствующий интеграл конечен.

Хорошо известно, что пространство прибанахово, а приквазибанахово. Поэтому достаточно установить, чтоявляется замкнутым подпространством пространствапри всех.

Предположим, что – последовательность из, а функциятакая, чтопри .

Докажем, что . Используя оценку (2.1), имеем:

.

Отсюда следует, что последовательность равномерно сходится внутрик некоторой функции. Учитывая теорему Ф. Рисса (см. [17]), нетрудно подобрать подпоследовательностьтакую, чтопочти всюду в. Поэтомупочти всюду в, и следовательно,. □

3. Интегральное представление гармонических функций

Пусть – множество всех гармонических вфункций;, то есть

.

В этом параграфе мы построим аналог представления (2.6) для функций из класса . Сначала заметим, что из (2.6) непосредственно следует представление

.

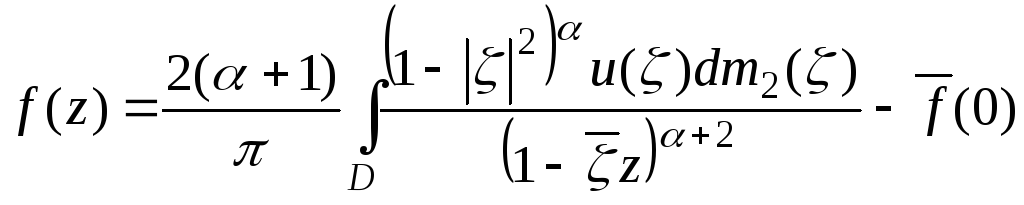Действительно, если , то по формуле (2.6)

. (7)

Но нетрудно увидеть, что

. (8)

Поэтому, суммируя равенства (7) и (8), окончательно получим:

.

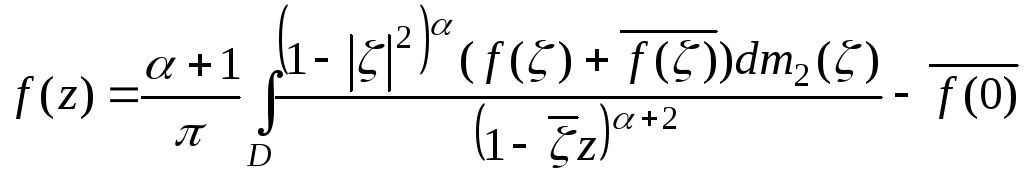Следовательно,

. (9)

Формула (9) является аналогом формулы Шварца для классов Харди Из (9) непосредственно вытекает:

. (10)

Суммируя формулы (9) и (10), получим:

(11)

Положим

,;

тогда из (11) имеем:

или

.

Но учитывая, что , окончательно получаем следующее утверждение:

Теорема 6. Пусть . Тогда справедливы следующие представления

а) ,

где .

б)

4. Ограниченные проекторы в пространствах ипри

Рассмотрим интегральный оператор в с ядром

:

.

Очевидно, что – аналитическая функция вдля произвольной функции, при условии, что, где

В этом параграфе мы дадим полную характеризацию тех , для которых справедливо представление (2.7) при некотором. С этой целью сначала докажем следующее элементарное утверждение.

Пусть, как и прежде, , где, при этом, также.

Лемма 1. Пусть , при этом, тогда справедливы оценки:

а) 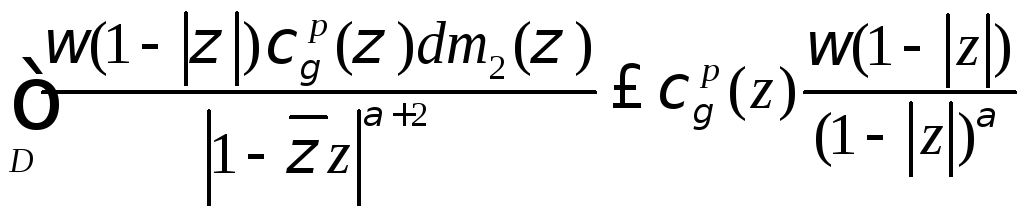при всех.

б) .

Напомним, что .

Доказательство. Положим

,

где . Учитывая тождество

и равенство

легко установить оценку

при .

Поэтому

.

Положим

.

Очевидно,

.

Нетрудно заметить, что

.

Интегрируя по частям в последнем интеграле, получаем:

.

Отсюда, учитывая что , выводим:

или

,

то есть

. (2.12)

Перейдём к оценке . Проводя аналогичные рассуждения, получаем:

Интегрируя в последнем интеграле по частям, приходим к равенству

,

то есть

.

Отсюда, учитывая, что , окончательно получаем:

(13)

Объединяя оценки (12) и (13), приходим к первому утверждению леммы. Теперь докажем неравенство б). В силу леммы 1 имеем:

.

Повторяя рассуждения части а) доказательства, приходим к оценке

. □

Следующее утверждение известно как тест Шура

Теорема 7. Пусть –-измеримое множество с неотрицательной меройна,– неотрицательная функция на, операторопределён на множестве-измеримых функцийследующим образом

,

причём функция такая, что интеграл сходится кпочти всюду.

Тогда если и существуют строго положительная-измеримая функциянаи числотакие, что

(14)

и

, (15)

где , то операторявляется ограниченным оператором на, причём

Доказательство. Фиксируем функцию . Используя неравенство Гёльдера, имеем:

.

С помощью неравенства (14) получаем

.

Откуда

.

Теперь, применяя теорему Фубини и меняя порядок интегрирования, получаем:

.

Далее, учитывая неравенство (15), окончательно выводим:

то есть . □

Теорема 8. Пусть , тогда оператор

(16)

отображает пространство на пространство.

Доказательство. Утверждение о том, что каждая функция из класса допускает представление (16), непосредственно следует из теоремы 4.

Остаётся установить, что при каждой функцияпринадлежит классу. Докажем указанное утверждение сначала при. Из равенства (16) имеем:

Изменив порядок интегрирования, получили:

Теперь, учитывая лемму 1, имеем:

.

Теорема доказана при .

Теперь предположим . В этом случае применим теорему 7 и лемму 1. Докажем, что если

,

, то все условия теоремы выполнены.

Действительно, условия (14), (15) непосредственно следуют из неравенств а), б) леммы 1. Следовательно, все условия теоремы 7 выполнены. □

Точно таким же образом устанавливается

Теорема 9. Пусть и, тогда оператор

отображает пространство на пространство.

Следующая теорема играет существенную роль при описании линейных непрерывных функционалы на пространствах .

Теорема 10. Пусть ,,. Тогда оператор

, ,

отображает пространство в пространствогде,.

Доказательство. Как и прежде, положим ,,. Тогда, применяя неравенство Гёльдера, получим:

. (2.17)

По лемме 2.1 отсюда имеем:

, .

Умножая последнее неравенство на , интегрируя пои учитывая последнюю оценку, выводим:

.

Преобразуя подынтегральное выражение первого интеграла, получим:

, .

Поэтому из оценки (2.17) имеем:

.

Снова используя лемму 2.1, окончательно получаем:

. □