Формула Коши

Теорема. Пусть D — область на комплексной плоскости с кусочно-гладкой границей , функция f(z) — голоморфна в и  — точка внутри области D. Тогда справедлива следующая формула Коши:

Док-во

. Г

Рассмотрим окружность S_ρ достаточно малого радиуса ρ с центром в точке z₀. В области, ограниченной контурами Γ и S_ρ подынтегральная функция не имеет особенностей и по интегральной теореме Коши интеграл от неё по границе этой области равен нулю. Это означает, что не зависимо от ρ имеем равенство:

Для расчёта интегралов по S_ρ применим параметризацию., φ Є Сначала докажем формулу Коши отдельно для случая f(z) = 1:

Воспользуемся ею для доказательства общего случая:

=

Так как функция f(z) комплексно дифференцируема в точке z₀, то:

Интеграл от равен нулю:

Интеграл от члена o(1) может быть сделан сколь угодно мал при . Но поскольку он от ρ вообще не зависит, значит он равен нулю. В итоге получаем, что

Формула Коши-Грина

f(z)=

ς=ξ+iμ z Є inf Г

Доказательство

окружность

G =

.z D ψ(ς)=, ςЄ

Г

=2i

==

=0

+

(2)

+=2i

ς-z=ε

ς=ε

dς=εi

==i

W= ε

ε

=i=2πif(z)

В равенстве (2) перейдем к пределу

-2πif(z)= 2i

f(z)=

Лекция № 4,5,7 -весовое пространство аналитических в круге функций

Пусть обозначим через– класс всех аналитических вфункций, для которых

.

Если , мы отождествимс классом ограниченных аналитических в круге функций.

Нетрудно заметить, что условие является необходимым условием для нетривиальности класса.

Если , тоопределяет норму на пространстве, а если, то – квазинорму на пространстве.

Непосредственно из неравенства Гёльдера следует, что , еслииесли

В дальнейшем, если не оговорено противное, будем предполагать, что , причем

Следующее утверждение позволяет определить рост модуля функции из класса .

Теорема 1. Пусть , тогда справедлива оценка

(1)

Доказательство. Пусть

.

Очевидно, что В силу субгармоничности функцииимеем:

(2)

или

Теперь заметим, что :

. (3)

И

Напомним, что

.

Положив , из последнего неравенства выводим:

Учитывая неравенство (2.2), получаем:

то есть

□

Следствие 1. Пусть , тогда справедлива оценка

(4)

Доказательство непосредственно выводится из теоремы 1. □

При ,, для краткости обозначим

Следствие 2. Пусть Тогда если, то

Доказательство. Действительно, если , то, используя оценку (4), непосредственно получаем:

□

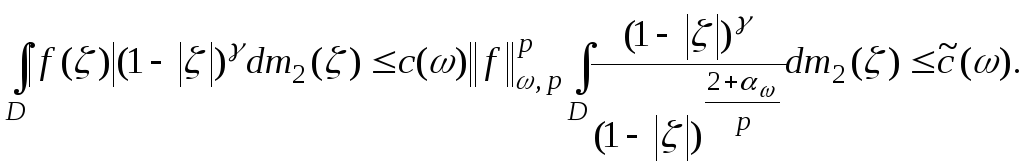Теорема 2. Пусть Тогда справедливо равенство

.

Доказательство очевидно, так как при всех

при этом

.

Докажем данную оценку. Имеем:

В последнем неравенстве мы использовали монотонность функции приУчитывая полученную оценку, имеем:

Поэтому из теоремы 1.7 непосредственно следует утверждение теоремы 2.2. □