Лекция № 1, 2

Представление в виде степенного ряда

Пусть U(z) – вещественная функция, гармоническая в круге . Тогда можно построить другую вещественную функциюV(z) , гармоническую в , такую что функция

F(z)=U(z)+iV(z)

Является аналитической в этом круге. Такая функция V называется гармонически спряженной с U, а функции U(z) и V(z) – сопряженными гармоническими функциями

U(z)=ReF(z)

F(z) разлагается в степенной ряд , который равномерно сходиться компактных множествах круга

Пусть , тогда

,

где

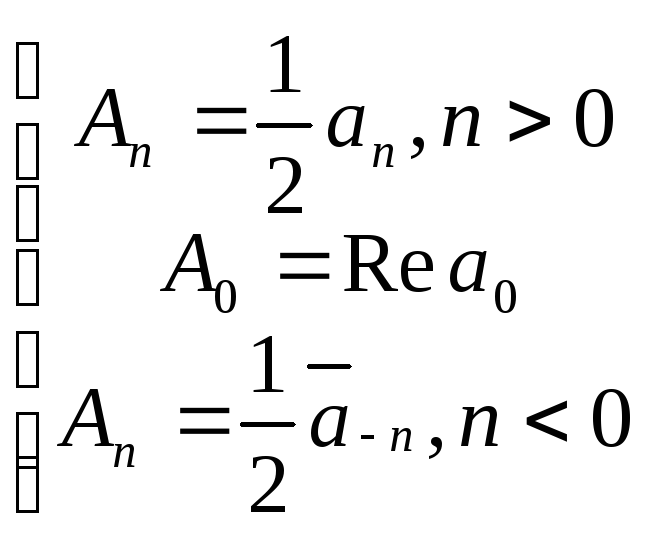
Таким образом, любая функция U(z), гармоническая в круге , допускает представление в виде ряда

Равномерно сходящегося на компактных подмножествах круга .

Формула Пуассона

Формулу, которую мы вывели в предыдущем пункте, можно записать в замкнутом виде.

Если R > 1, то мы легко находим, что при r < 1

Суммируя две геометрические прогрессии, получаем

при

Таким образом, мы приходим к представлению Пуассона: если U(z) — гармоническая функция в {|z| <.R}, где R>1, то при имеет место формула

Эта формула является фундаментальной для всей теории. Мы сейчас увидим, что она справедлива при намного более общих условиях, чем указанное выше. Функция

Называется ядром Пуассона для круга {|z|<1}.

Представление Пуассона для гармонических функций Представление Пуассона для гармонических функций, принадлежащих некоторым классам

Пусть известно лишь, что функция U(z) гармонична в круге {|z| < 1}. Замечательно, что часто её всё же можно представить в этом круге по формуле Пуассона.

Теорема. Пусть р > 1, и пусть V (г) — гармоническая функция в {\z\ < 1}. Предположим, что средние

ограничены при r<.1. Тогда существует такая функция , что

для г < 1,

Доказательство.

При р > 1 пространство является cопряжённым с , где. Для функций(вместоподходит любая последова­тельность, стремящаяся к 1 снизу) имеем (здесь, конечно, берётся по отрезку (—π,π)), так что канторовским диагональным процессом мы можем выделить из них подпоследовательность Un_h такую что для всех функций G, пробегающих некоторое счётное всюду плотное подмножество пространства , существует предел

Так как , то этот предел LG на самом деле существует для всех иLG является ограниченным линейным функционалом на L^q. Следовательно, поскольку пространство L^p сопряжено с L^q, то существует такая функция , что

всех .

Теперь, для каждого п функция гармонична в, так что еслиr < 1, то

Зафиксируем произвольное r <. 1 и любое θ и возьмём G (t) = . Тогда

В этом равенстве слева стоит

Таким образом,

,

где

Замечание Тот же результат справедлив с тем же доказательством и при р =∞, если мы немного изменим формулировку теоремы:

Теорема. Если U(z) — ограниченная гармоническая функция в {|z| < 1}, то существует функция , такая что

А что же в случае р=1? Пространство , к сожалению, не является сопряжённым ни с каким другим. Но М — пространство конечных вещественных мер μ на [-π, π] с нормой ||μ||, равной полной вариации меры μ,— сопряжено с С [-π, π] —пространством непрерывных функций на [-π, π]. Если , то мы можем связать сg меру μ, положив

при этом .

Теперь рассуждение, проведенное при доказательстве первой теоремы этого пункта, показывает, что справедлива такая

Теорема. Если U(z)—гармоническая функция в круге {|z|< 1} и средние

ограничены при r< 1, то существует конечная вещественная мера μ на [-π, π], такая что

для 0≤r< 1.

Следствие (Званс). Пусть U(z)-функция, гармоническая и положительная (здесь и далее «положительный» означает «неотрицательный») в круге {|z|<1}. Тогда существует конечная положительная мера μ на [-π, π],, такая что

Доказательство.

Для r<1 (используя, например, разложение , имеющее место в {|z| < 1}) получаем

,

гак как . А теперь применяем теорему. Мера μ положительна, потому что в этом случае (см. опять доказательство первой теоремы этого пункта) оказывается, что интеграл положителен для любой положительной функции как предел положительных чисел!

Граничное поведение

Если мы имеем одно из представлений

выведенных в предыдущем пункте, то возникает задача нахождения связи между U(z) и функцией F(t) или мерой dμ(t).