учебники / Менеджмент_Абчук В.А_Учебник_2002 -463с

После преобразований получим х2 + 25х - 150 = 0.

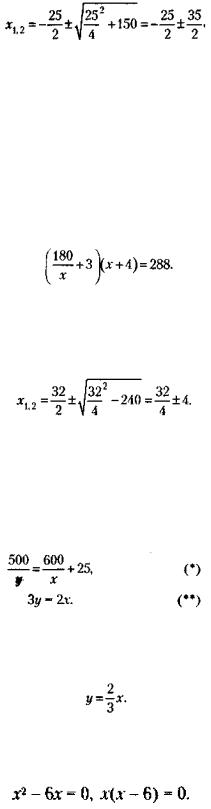
Решая квадратное уравнение по стандартной формуле, получим:

х1 = 5 участков (х2 не подходит, так как отрицательно).

Следовательно, 1) количество участков, нарезанных в первой части земли, равно 5, а во второй – 5 + 15 = 20; 2) площадь участка в первой части земли равна 2 га, а во второй – 1 га.

101. Обозначая первоначальное количество линий через х, можно представить условие задачи в следующем виде:

После преобразований получим х2 - 32х + 240 - 0.

Решая квадратное уравнение по стандартной формуле, получим:

Задача имеет два решения: х1 = 20, х2 = 12.

102. Обозначая через х старый, а через у новый расход сырья на один комплект мебели, можно записать условия задачи следующим образом:

Решая систему из двух уравнений с двумя неизвестными, из (**) получим

Подставляя значение у в (*), после преобразований получим:

Откуда х1 = 0 (не подходит, так как отрицательно), х2 = 6.

Следовательно, раньше расходовалось на один комплект мебели 6 м2 древесины, а теперь

551

.

103.Обозначая через х количество калийного удобрения в 100 кг смеси, а через

уколичество калийного удобрения, которое нужно добавить к ней, можно записать условие задачи следующим образом:

Решая систему уравнений, получим у = 50 кг.

104. Обозначая через х среднюю скорость первого автомобиля, а через у среднюю скорость

второго автомобиля, можно записать условие задачи следующим образом:

Решая систему из двух уравнений с двумя неизвестными, получим:

Решая квадратное уравнение по стандартной формуле, получим:

х1 = 240 (х2 не подходит, так как отрицательно). Итак, средняя скорость первого автомобиля равна 240 км/ч, а второго 240 - 60 = 180 км/ч.

105. Вопрос: «Соответствует ли ваша правдивость честности компании?» Правдивый представитель при честной сделке на этот вопрос ответит «да», а при нечестной – «нет»; лживый же будет отвечать противоположно истине: если честность сделки и правдивость представителя не совпадают, он вместо «нет» ответит «да», и наоборот.

Возможные ситуации и соответствующие ответы сведены в следующую таблицу:

552

Из таблицы видно, что каким бы ни был представитель компании, положительный ответ всегда говорит о честности сделки, а отрицательный – о ее нечестности.

106. Обозначим через х уменьшение годового дохода предприятия в результате повышения цены на товар с у на z у. д. ед. и соответствующего падения объема продаж. Тогда условие задачи будет математически выглядеть так:

Учитывая, что до повышения цены имело место равенство

найдем у = 8 у. д. ед. Тогда из (2) следует, что

откуда

Из (1) следует, что

Следовательно, увеличение цены на товар и соответствующее уменьшение объема продаж (спроса) не привело к изменению годового дохода предприятия.

107. Обозначая через х объем продаж до его падения, а через у –

553

соответствующую цену товара, запишем условие задачи следующим образом:

или, что то же самое,

1)Из (2) следует 6 х 2 = (6 + у) 2, откуда у = 6.

2)Из (1) следует, что х может быть любым, так как на него можно сократить обе части уравнения:

108. Обозначим величину уценки через х раз, тогда условие задачи будет выглядеть так:

Откуда

Следовательно, в результате первой уценки цена домика будет установлена:

а в результате второй:

109. Обозначая через х стоимость грузовой автомашины, а через у стоимость станка, купленного компаньоном А, нетрудно установить, что стоимость легковой автомашины равна у, а стоимость станка, приобретенного компаньоном Б, составляет х – 2.

Из условия задачи также следует, что х + у = 24 и суммарная стоимость автомашины тоже равна 24 тыс. у. д. ед.

554

Следовательно, если бы легковая автомашина была в три раза дороже грузовой, то они должны были бы стоить соответственно 18 и 6 тыс. у. д. ед. и равенство затрат компаньонов можно было бы записать так:

Откуда

Итак:

1)Стоимость покупок: станок, купленный компаньоном А, – 17 тыс. у. д. ед., купленный компаньоном Б, – 5 тыс. у. д. ед.; стоимость грузовой автомашины – 7 тыс. у. д. ед., легковой – 17 тыс. у. д. ед.

2)Всего было потрачено: компаньоном А 17 + 7 = 24 тыс. у. д. ед., компаньоном

Б5 + 17 = 22 тыс. у. д. ед.

110. Обозначим через х торговую наценку (в долях от 1), через у – стоимость товара без наценки и через z – сумму комиссионных агенту по продаже. Тогда условие задачи можно записать так:

1)Величину торговой наценки найдем из (1):

2)Из (2) следует, что стоимость оставшегося товара без торговой наценки (товар не продан) равна:

а стоимость проданного товара без учета торговой наценки –

Отсюда прибыль равна:

555

3) Из условий задачи:

Откуда z = 18 тыс. у. д. ед., а в процентах

111. Обозначим через х стоимость всех кроватей, через у – всех туалетных столиков, а через z – стоимость одной кровати. Тогда условия покупки первой партии товара можно записать так:

Если бы в первой партии было решено приобрести только туалетные столики, то выражение (*) приобрело бы следующий вид:

а умножение на 32 – увеличение количества столиков, пропорциональное уменьшению цены каждого.

Следовательно,

откуда у = 30.

Подставляя это значение в (*), получим х = 30.

Обозначим через т стоимость одной кровати. Тогда один столик будет стоить

23 z.

При этом исходя из условия задачи будет иметь место соотношение

556

Подставляя значения х и у и решая относительно z, получим:

Следовательно:

1) Общая стоимость закупленных кроватей и столиков в первой партии равна соответственно – из (*):

а во второй партии:

2)Стоимость кровати равна 3 тыс. у. д. ед., а стоимость туалетного столика

3)Количество кроватей и столиков, закупленных в первой и второй партиях, соответственно равно:

в первой партии – кроватей 63 = 2 единицы, столиков 102 = 5 единиц; во второй

партии – кроватей 243 = 8 единиц, столиков 202 =10 единиц. Всего 10 кроватей и 15 столиков.

112. Обозначим через х общий объем выпивки в литрах или равный ему вес закуски в килограммах. Тогда суммарная стоимость выпивки будет 20х у. д. ед., а закуски – 10х у. д. ед. и общие затраты составят:

Если бы эти затраты были равными для выпивки и закуски, то и на одно, и на другое пришлось бы по 302х 15ху. д. ед. Исходя из этого, условие задачи можно записать так:

557

откуда

х= 12 л выпивки или 12 кг закуски. Следовательно:

1)Было закуплено 12 л выпивки и 12 кг закуски.

2)Стоимость выпивки равна 12 х 20 = 240 у. д. ед., стоимость закуски – 12 х 10 = 120 у.д.ед.

3)Всего потрачено 240 + 120 = 360 у. д. ед.

113. Обозначим через х фактическую цену продажи партии товара. При этом цена его покупки будет 1,х4 . Если бы товар был куплен на 30 % дешевле, цена

покупки составила 1,х4 0,7 . Продажа этого товара по цене на 60 % дороже цены покупки была бы равна в этом случае

Итак, условие задачи можно записать следующим образом:

откуда

Следовательно:

1)Партия товара была продана за 200 тыс. у. д. ед., а единица товара стоила

2)Цена покупки партии товара равна

114. Обозначим через х сумму, выделенную фирмой для закупки компьютеров,

558

через у – равные количества компьютеров обоих видов (при первом варианте закупки); через z – количество компьютеров вида «МА» и w – вида «МБ» (при втором варианте закупки).

При этом условие задачи можно записать так: первый вариант закупки:

второй вариант закупки:

Из уравнения (1) следует, что общее количество закупленных компьютеров по первому варианту равно:

Из уравнения (2) следует, что общее количество закупленных компьютеров по второму варианту равно:

По второму, более выгодному, варианту может быть закуплено компьютеров больше, чем по первому, на

Иными словами, при закупке по второму варианту фирма дополнительно (по сравнению с первым вариантом) бесплатно получает на каждые 120 компьютеров еще один.

115. Обозначим через х, у, z количество купленных компьютеров, телефонов и столов соответственно.

Тогда условие задачи можно записать так:

или после умножения левой и правой частей на 4:

559

Вычитая (2) из (1), получим:

откуда

Из (3) следует, что, во-первых, х может быть равен только 2, так как z и x должны быть целыми положительными числами, во-вторых, х не может быть равен 1, так как при этом z становится равным 53, что противоречит условию (всего куплено 30 предметов), и, в-третьих, х не может быть больше 2, так как при этом z становится отрицательным.

Итак, х = 2 единицам.

Из (3) следует, что z = 90 – 37 x 2=16 единиц, из (2) следует, что у = 30 – 2 – 16 =12 единиц.

116. Обозначим через х и у стоимость единиц товара А и Б соответственно. Тогда условие задачи можно записать так:

Решим систему из двух уравнений с двумя неизвестными, для чего умножим правую и левую часть уравнения (1) на 7, а уравнения (2) на 5:

Вычитая второй результат из первого, получим:

Из (1) следует, что

117.Обозначим через х и у соответствующее количество компонентов «Радость»

и«Сладость» в 50 литрах коктейля. Тогда условие задачи можно будет записать

560