учебники / Менеджмент_Абчук В.А_Учебник_2002 -463с

Поскольку для последней пары, где Чn = 0, Нn = 6 - 0 = 6, а для первой пары Н1 может быть минимально равно 0, при этом Ч1 = 6 - 0 = 6.

По условиям задачи от пары к паре количество производственных помещений для нечетных предприятий увеличивается на единицу, в распределении может участвовать всего 7 пар (имеющих Нn от 0 до 6, включая 0), т. е. 7 х 2 = = 14 малых предприятий. При этом в соответствии с (*):

Итак:

1)Ресурсы могут распределяться между 14 малыми предприятиями.

2)Всего распределяется 42 производственных помещения. Торговых точек для уравнивания возможностей МП должно быть столько, чтобы у каждого предприятия было по 6 единиц ресурсов, т. е. каждая пара предприятий должна получить по 6 торговых точек, а всего 6 x 7 пар предприятий = 42 торговые точки.

3)Количество ресурсов обоих видов, полученных каждым предприятием, будет следующим:

30.Оказывается, это довольно просто. Дело в том, что, к счастью аудитора, суммы цифр в обоих слагаемых оказались кратны 9, а значит – слагаемые делятся на 9. Естественно, делились на 9 они и до перестановки в них цифр. При сложении же чисел, делящихся на 9, сумма также делится на 9. Это означает, что сумма цифр результата сложения должна быть кратна 9. Сложив цифры суммы (кроме подделанной), получим 30. Ближайшее большее число, кратное 9, это 36. Нам не хватает 36 - 30 = 6. Следовательно, исправленная цифра – это 6.

31.Обозначим через х площадь арендуемого фирмой помещения, а через у – количество единиц продукции, идущих в уплату аренды. Тогда условие задачи можно записать так:

521

32. Обозначим через т, п, р, q количество контейнеров, поставляемых фирмами первой четверки (не обязательно в порядке последовательности фирм), которые являются партнерами соответствующих (в порядке номеров) фирм второй четверки (т - поставка партнера фирмы № 5, п - фирмы № 6 и т. д.). При этом условие задачи можно записать так:

(44 –это разность общего количества контейнеров и 20 – числа контейнеров, поставляемых первой четверкой: 2 + 4 + 6 + 8 = 20).

Умножая обе части (2) на 2, получим:

Из последнего выражения следует, что q может быть равно только 4, ибо по условиям задачи:

1)q, m,p должны быть целыми положительными числами,

2)эти числа различны и могут быть только 2, 4, 6, 8,

3)2 не подходит, так как при этом т = р,

4)6 и 8 не подходят, так как при этом т - р>8.Итак, q = 4. Тогда из (*) следует, что 2(4-2) = m-р, т- р = 4.

Последняя разность может иметь место лишь при следующих значениях пары т

ир:

522

Первая пара не подходит, так как число 4 уже имеет «хозяина» – ему равно q. Следовательно, т = 6р = 2.

Для п остается лишь значение, равное 8.

Если выстроить значение этих показателей по ранжиру (р, q, т, п), то эта последовательность и будет соответствовать последовательности номеров фирм- партнеров из второй четверки фирмам первой четверки (где была последовательность т,п,р,q):

фирма № 5 является партнером фирмы № 3, фирма № 6 является партнером фирмы № 4, фирма № 7 является партнером фирмы № 1, фирма № 8 является партнером фирмы № 2.

Подставляя соответствующие значения в (1), нетрудно рассчитать количество контейнеров, поставляемых фирмами второй четверки.

Итоговые данные по поставкам всеми фирмами будут следующими:

33. Обозначим начальные фонды, равные у обоих предприятий, через х. Тогда к моменту окончания первой операции предприятие А обладало фондом в размере, равном х + 30, а предприятие Б – х - 30 тыс. у. д. ед. К моменту окончания второй операции фонд предприятия А составлял:

523

34. Взнос предпринимателя В, равный 320 тыс. у. д. ед., составляет 1 прежнего

3

складского капитала. Значит, весь этот капитал был равен 320 х 3 = 960 тыс. у. д. ед. Причем в этом капитале доли А и Б относились как 1,5 : 1, т. е. были соответственно равны 576 и 384 тыс. у. д. ед.

Теперь нужно разделить сумму, равную взносу В, между А и Б так, чтобы у

каждого из них оказалось по 1 от нового складского капитала, который будет так

3

же, как и старый, равен 960 тыс. у. д. ед. (взнос В не войдет в этот капитал, так как будет роздан А и Б). Для этого нужно вернуть предпринимателю А столько денег, чтобы его доля после этого оказалась равной 960 : 3 = 320 у. д. ед. Иными словами, он должен получить 576 - 320 = 256 тыс. у. д. ед. Предприниматель Б должен получить 384 - 320 = 64 тыс. у. д. ед.

35. Обозначим через длину отрезка проволоки, причитающейся владельцу Б. Тогда условие задачи можно будет записать так:

Решая это уравнение, получим:

Владельцу А будет причитаться:

524

36. Обозначим через х стоимость месячного содержания помещений. Тогда условие задачи можно записать так:

Откуда, после преобразований, х = 150 тыс. у. д. ед.

Вычитая полученную стоимость содержания помещений из дохода, получим величину ежемесячных потерь арендатора:

37. Обозначим через х количество участков для субаренды. Тогда выручка за субаренду составит 8х,годовой заработок будет равен

и условие задачи запишется так:

После преобразований получим:

Решая квадратное уравнение по стандартной формуле, получим:

Следовательно:

1)Количество участков равно 12.

2)Прибыль арендатора равна:

38.Обозначим через Ст, Ср и Мл обобщенных представителей старших, средних

имладших владельцев каждой группы. Тогда по условиям задачи:

525

Это равнозначно следующим обозначениям:

так как, подставляя значения из (2) в (1), получаем тождество:

Далее, вводя новые обозначения, можно показать, что имеют место следующие равенства:

(3)

так как, подставляя значения из (3) в (2), получаем тождество:

Обозначим

Тогда с учетом (2) и (3) можно записать:

Подбираем значения m и n исходя из следующих условий:

–т > п (иначе z будет отрицательным или равным 0, что противоречит условиям задачи);

–т и п должны быть целыми положительными числами разной четности (разная четность т и n объясняется так: 1) из Ср2 = х2 + у2 следует разная четность х

иу – сторон прямоугольного треугольника; 2) поскольку у = 2ху в любом случае четен, х должен быть нечетным; 3) чтобы х был нечетным, необходимо, чтобы тип, связанные с х зависимостью х = т2 - п2, были разной четности);

–т и п должны удовлетворять условию х1 + у1 = Ср2 (из х2 + у2 должен без остатка извлекаться квадратный корень):

Наименьшей возможной парой т и п, удовлетворяющей всем этим условиям, является пара 8 и 7. При этом

526

Поскольку по условиям задачи минимальная доля (2 тыс. у. д. ед.) принадлежит младшему афганцу, ему причитается и наименьшая премия, равная 2'2 = 4 тыс. у. д. ед. Откуда премия среднего афганца равна:

а старшего афганца –

Соответственно их доли составляют:

Доля средней сестры равна:

а ее премия –

Премия младшей сестры равна:

а старшей–

Соответственно их доли составляют:

Доля старшего брата равна:

127 - 33 = 94 тыс. у. д. ед.,

а его премия – 942 = 8836 тыс. у. д. ед. Премия среднего брата равна:

527

8836 - 3360 = 5476 тыс. у. д. ед,

а младшего брата –

5476 - 3360 = 2116 тыс. у. д. ед.

Соответственно их доли составляют:

39. Обозначим общее количество отечественных и иностранных фирм через х (при этом х должен быть целым, положительным и четным числом). Тогда каждая фирма должна израсходовать

При этом х может быть 2, 4, 6...

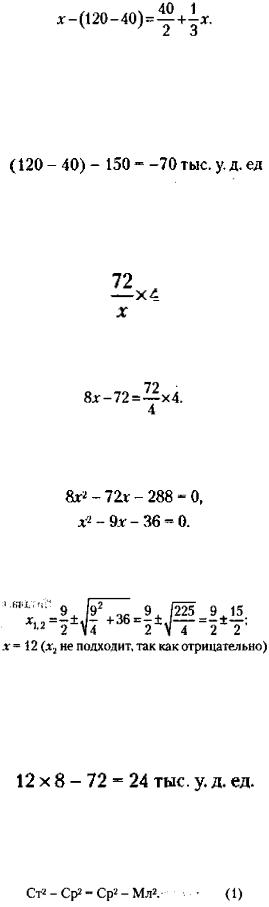
С учетом того, что конструкция А стоит 1 тыс. у. д. ед., конструкция Б – а конструкция В –будем рассуждать так:

х = 2 отпадает, так как речь идет о ряде как отечественных, так и иностранных фирм;

х = 4 также не проходит, так как при этом каждая фирма способна тратить 9 4

тыс. у. д. ед. и не может на эти деньги купить целое число конструкций всех видов;

при х = 6 расходы каждой фирмы составили На эти деньги

можно купить по одной конструкции вида А, по одной конструкции вида Б и по одной – вида В:

Это и будет ответом на первый вопрос.

Общее количество фирм, участвующих в покупке, равно 6 (3 отечественные и 3 иностранные).

40. Обозначая момент проверки постов охраны через х1 можно математически записать условие задачи так:

528

Решая это уравнение, получим:

41. Вероятность получения счастливого билета (Р) может быть определена по следующей формуле из теории вероятностей:

Этот расчет можно проверить, собрав достаточное количество (порядка тысячи) любых билетов с шестизначными номерами и сосчитав, сколько счастливых приходится в среднем на сотню. Должно получиться 5–6 билетов.

42. 1) Обозначим через О, М и Д возраст отца, матери и дочери в момент заключения страхового договора. При этом условие задачи математически запишется так:

вмомент заключения договора,

вмомент заключения договора,

вмомент выплаты страховой премии (через М лет). Из (2) следует, что О = 12Д.

Подставляя значение О в (3), получим:

Подставляя значение О и М в (1), получим: 12Д + 10Д + Д = 46, откуда Д - 2 года, О = 12Д = 24 года, М = 10Д = 20 лет.

2) Страховая премия должна быть выплачена через М = 20 лет после заключения договора.

529

43. Обозначим через х первоначальное количество работников в каждом малом предприятии, а через у – первоначальное количество этих предприятий. Тогда количество предприятий после первой реорганизации будет у -10, а количество работников в каждом из них х + 1. После второй реорганизации получим соответственно у – 10 - 15 = у - 25 предприятий и х+ 1 + 2 = х + 3 работника в каждом.

При данном условии задачи можно записать так:

Из (1) следует:

Совместно решая (1) и (2), получим:

Подставляя (*) в (**), получим:

Общая численность работников объединения равна:

44. Обозначим время от полудня до противостояния стрелок через х, а число делений, проходимых часовой стрелкой от цифры 12 до момента противостояния,

– через у.Тогда условие задачи можно записать следующим образом:

530