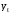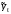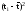Контрольная Эконометрика

;

;

;

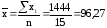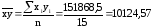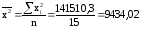
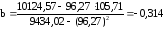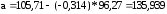
Рассчитываем для каждого значения х значения у_х. Заносим в таблицу.

Критерий Дарбина-Уотсона:

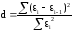
yi	yx	ei = y-yx	(ei – ei-1)2	ei 2
101,7	113,71	-12,01	-	144,24
101,1	104,95	-3,85	66,59	14,82
100,4	105,20	-4,80	0,90	23,04
100,1	104,66	-4,56	0,06	20,79
100	105,76	-5,76	1,44	33,18
100,1	103,47	-3,37	5,71	11,36
100	105,95	-5,95	6,66	35,40
105,8	103,63	2,17	65,93	4,71
145	111,57	33,43	977,19	1117,56
99,8	103,82	-4,02	1402,50	16,16
102,7	103,63	-0,93	9,55	0,86
109,4	97,29	12,11	170,04	146,65
110	112,61	-2,61	216,68	6,81
106,4	106,77	-0,37	5,02	0,14
103,2	102,66	0,54	0,83	0,29
Сумма			2929,09		1576,03

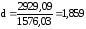
Так как значение критерия Дарбина-Уотсаона близко к 2,0, то можно считать что автокорреляция почти отсутствует.

Задача 5

В таблице приводятся данные о динамике выпуска продукции Финляндии (млн. долл.).

Задание:

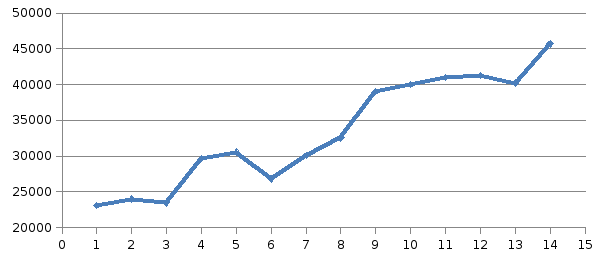
1. Постройте график временного ряда

2. Найдите коэффициенты автокорреляции (для лагов r = 1; 2) данного ВР.

3. Найдите уравнение тренда ВР y_t, предполагая, что он линейный, и проверьте его значимость на уровне α=0,05

4. Дайте точечный и интервальный (с надежностью 0,95) прогнозы выпуска продукции на момент n+1

Год	yt, млн. долл.
1991	23085
1992	23980
1993	23444
1994	29657
1995	30570
1996	26800
1997	30100
1998	32560
1999	39020
2000	40012
2001	41010
2002	41250
2003	40200
2004	45680

Решение.

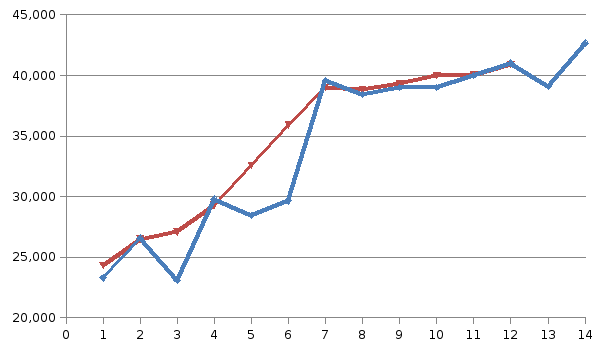
Построим график временного ряда

Год	t	yt, млн. долл.
1991	1	23085
1992	2	23980
1993	3	23444
1994	4	29657
1995	5	30570
1996	6	26800
1997	7	30100
1998	8	32560
1999	9	39020
2000	10	40012
2001	11	41010
2002	12	41250
2003	13	40200
2004	14	45680

Для обнаружения тенденции в данном ВР воспользуемся критерием «восходящих и нисходящих» серий.

1) Для исследуемого ВР определяется последовательность знаков, исходя из условий: (+) при y_t+1–y_t > 0, (-) при y_t+1–y_t < 0. При этом, если последующее наблюдение равно предыдущему, то учитывается только одно наблюдение.

2) Подсчитывается число серий ν(n). Под серией понимается последовательность подряд расположенных плюсов или минусов, причем один плюс или один минус считается серией.

3) Определяется протяженность самой длинной серии l_max(n).

4) Значение l(n) находят из следующей таблицы:

Длина ряда, n	n≤26	26<n≤153	153<n≤170
Значение l(n)	5	6	7

5) Если нарушается хотя бы одно из следующих неравенств, то гипотеза об отсутствии тренда отвергается с доверительной вероятностью 0,95

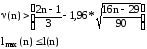
Определим последовательность знаков:

t	Выпуск продукции, yt млн.долл.	δ
1	23 298
2	26 570	+
3	23 080	-
4	29 800	+
5	28 440	-
6	29 658	+
7	39 573	+
8	38 435	-
9	39 002	+
10	39 020	+
11	40 012	+
12	41 005	+
13	39 080	-
14	42 680	+

Определим число серий ν(n) = 9. Определим протяженность самой длинной серии l_max(n) = 4, l(n) = 5, так как n=14<26. Проверим выполнение неравенств:

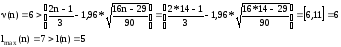
Второе неравенство не выполняются, следовательно, тренд (тенденция) в динамике выпуска продукции имеется на уровне значимости 0,05.

Среднее значение 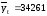млн.долл.

 Среднее значение 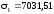 млн.долл.

Вычислим коэффициенты автокорреляции первого и второго порядков, то есть для лагов τ =1;2. Подготовим данные для вычисления коэффициентов автокорреляции первого и второго порядков. Дополним таблицу данных двумя столбцами Y_t-1 и Y_t-2 .

t	Yt	Yt-1	Yt-2
1	23 298	-	-
2	26 570	23 298	-
3	23 080	26 570	23 298
4	29 800	23 080	26 570
5	28 440	29 800	23 080
6	29 658	28 440	29 800
7	39 573	29 658	28 440
8	38 435	39 573	29 658
9	39 002	38 435	39 573
10	39 020	39 002	38 435
11	40 012	39 020	39 002
12	41 005	40 012	39 020
13	39 080	41 005	40 012
14	42 680	39 080	41 005

r₁ = 0,85188.

R₂ = 0,8343.

Высокое значение коэффициента автокорреляции первого порядка r₁=0,85 свидетельствует об очень тесной зависимости между выпуском продукции текущего и непосредственно предшествующего годов, и, следовательно, о наличии в исследуемом временном ряде сильной линейной тенденции.

Исследуемый ряд содержит только тенденцию, так как наиболее высоким оказался коэффициент автокорреляции первого порядка (0,85>0,83).

Скользящие средние найдем по формуле: 

,

здесь m=2p-1.

При m=3, p=1

Вычисляем: 

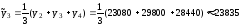
и так далее.

Результаты вычислений занесем в таблицу и построим графики исходного 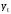и сглаженного 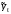 рядов в одной координатной плоскости.

t
1	23 298
2	26 570	24 315,76
3	23 080	26 483,07
4	29 800	27 106,40
5	28 440	29 299,04
6	29 658	32 556,67
7	39 573	35 888,31
8	38 435	39 002,94
9	39 002	38 818,61
10	39 020	39 344,27
11	40 012	40 011,93
12	41 005	40 031,93
13	39 080	40 921,26
14	42 680

Параметры (коэффициенты) уравнения тренда.

	Коэффициенты
Y-пересечение	22686,54945
t	1543,250549

Анализ данных таблицы дисперсионного анализа показывает, что получено статистически значимое уравнение, так как наблюдаемое значение F=52,785, превышает его табличное значение F_таб(0,05;1;12)=4,75, t_таб(05;12)=2,1788.

Таким образом, параметры уравнения тренда статистически значимы на уровне α=0,05: уравнение тренда можно использовать для прогноза.

Сделаем точечный и интервальный (с надежностью 0,95) прогнозы среднего и индивидуального значений прогнозов на 2003 год.

Определим точечный прогноз:

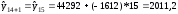млн.долл

Вычислим интервальный прогноз.

Так как тренд является прямой, то доверительный интервал можно представить в виде: 

Здесь стандартная ошибка предсказания по линии тренда 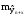вычисляется по формуле:

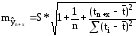
Здесь величина S является стандартной ошибкой регрессии, и ее значение находится в таблице Регрессионная статистика

Стандартная ошибка

1637,180026

t(0,05;12)=2,1788.

Итак, по условию задачи: t_n+x=15, n=14

Для вычисления стандартной ошибки предсказания по линии тренда 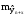необходимо вычислить 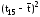 и сумму .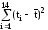

t	yt
1	23 298	42,25
2	26 570	30,25
3	23 080	20,25
4	29 800	12,25
5	28 440	6,25
6	29 658	2,25
7	39 573	0,25
8	38 435	0,25
9	39 002	2,25
10	39 020	6,25
11	40 012	12,25
12	41 005	20,25
13	39 080	30,25
14	42 680	42,25
7,5	Сумма	227,5

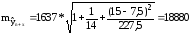(млн. долл.)

Максимальная ошибка прогноза будет равна:

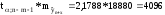 (млн. долл.).

Нижняя граница прогноза имеет значение:

20111,2 – 4096 = 16014 (млн. долл.)

Верхняя граница прогноза имеет значение:

20111,2 + 4096 =24707 (млн. долл.)

Вывод:

1) значение выпуска продукции Финляндии в 2003 составит 20111,2 млн. долл.

2) с надежностью 0,95 данное значение будет находиться в интервале (16014; 24207) млн. долл.

Список используемой литературы

1. Доугерти К. Введение в эконометрику / К. Доугерти М., Финансы и статистика, 1999 2. Эконометрика. Учебник. Под ред. Елисеевой И.И. М., Финансы и статистика, 2002 3. Пахнутов И.А. Введение в эконометрику. Учебное пособие - Калининград. Издательство КГТУ, 2005