Контрольная Эконометрика

Задача 1

Имеются данные об уровне механизации работ Х (%) и производительности труда У (т/ч) для 12 предприятий:

Xi	30	32	36	40	41	46	52	54	61	55	61	67
Yi	23	20	27	32	30	33	34	36	38	40	41	43

По данным, приведенным в таблице:

1. построить линейное уравнение парной регрессии у на х;

2. рассчитать линейный коэффициент парной корреляции и оценить тесноту связи;

3. оценить статистическую значимость параметров регрессии и корреляции, используя F-статистику, t-статистику Стьюдента и путем расчета доверительных интервалов для каждого из показателей;

4. вычислить прогнозное значение у при прогнозном значении х, составляющем 108% от среднего уровня;

5. оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал;

6. полученные результаты изобразить графически и привести экономическое обоснование.

Решение.

1. Линейная модель регрессии

Уравнение парной регрессии:

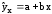
где а и b – параметры уравнения

;

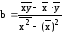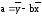
Составим вспомогательную таблицу.

i	x	y	xy	x2	(xi-x)2	(yi-y)2	yx	yi-yx	(yi-yx)2
1	30	23	690	900	321,13	101,61	19,08	3,92	15,37
2	32	20	640	1024	253,45	171,09	17,39	2,61	6,81
3	36	27	972	1296	142,09	36,97	21,32	5,68	32,26
4	40	32	1280	1600	62,73	1,17	24,13	7,87	61,94
5	41	30	1230	1681	47,89	9,49	23,01	6,99	48,86
6	46	33	1518	2116	3,69	0,01	24,70	8,30	68,89
7	52	34	1768	2704	16,65	0,85	25,26	8,74	76,39
8	54	36	1944	2916	36,97	8,53	26,38	9,62	92,54
9	61	38	2318	3721	171,09	24,21	27,51	10,49	110,04
10	55	40	2200	3025	50,13	47,89	28,63	11,37	129,28
11	61	41	2501	3721	171,09	62,73	29,19	11,81	139,48
12	67	43	2881	4489	364,05	98,41	30,32	12,68	160,78
S	575,0	397,0	19942	29193	1640,96	562,96	-	-	942,64

;

;

;

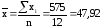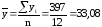
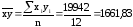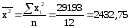
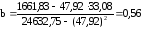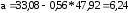
Рассчитываем для каждого значения х значения у_х. Заносим в таблицу.

2.Линейный коэффициент парной корреляции.

Если: 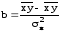умножить на 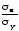, то получим:

,

Значит, коэффициент корреляции можно находить по формуле

;

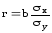
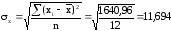r² = 0,914

Так как значение коэффициента корреляции близко к 1, то связь признается очень тесной, почти функциональной.

Найденное значение индекса детерминации говорит, что 91,4% вариации производительности труда (Y) объясняется вариацией фактора x – уровнем механизации работ.

3. Оценка статистической значимости параметров регрессии

Оценку статистической значимости параметров регрессии проведём с помощью t-статистики Стьюдента и путём расчёта доверительных интервалов для каждого из показателей. Выдвинем гипотезу Н_о: о статистически незначимом отличии показателей от нуля, то есть Н_о : a = b = r_xy = 0. По таблицам t-критерия Стьюдента при 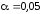и числу степени свободы в данном случае равном : n – 2 = 12 – 2 = 10 находим t_табл = 2,23.

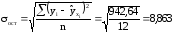
Фактические значения t-критерия определяются по формулам:

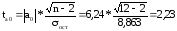≈2.23

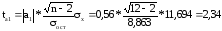>2.23

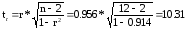>>2.23

Из выше найденных фактических значений t_a, t_b, t_r, видим что кроме параметра а они больше ранее найденного табличного (критического) значения критерия Стьюдента (t = 2,23) следовательно гипотеза Н_о – отклоняется, то есть a, b и r_xy не случайно отличны от нуля.

Найдем F-статистику для оценки значимости уравнения регрессии (n=12, m=1).

Табличное значение критерия со степенями свободы k₁=1 и k₂=10, F_табл = 4,96. Так как F > Fтабл, то уравнение парной регрессии признается статистически значимым и модель адекватной.

Доверительные интервалы для параметров уравнения регрессии:

Несмещенной оценкой дисперсии возмущений является величина:

S²_y = 4.81 - необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).

S_y = 2.19 - стандартная ошибка оценки (стандартная ошибка регрессии).

S_a - стандартное отклонение случайной величины a.

S_b - стандартное отклонение случайной величины b.

Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:

(b - t_крит S_b; b + t_крит S_b)

(0.56 - 2.228 • 0.0542; 0.56 + 2.228 • 0.0542)

(0.44;0.68)

С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.

(a - t_крит S_a; a + t_крит S_a)

(6.25 - 2.228 • 2.67; 6.25 + 2.228 • 2.67)

(0.29;12.2)

С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.

4. Прогнозное значение у при прогнозном значении х, составляющем 108% от среднего уровня

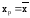× 1,08= 47,92 × 1,08 = 51,75

Прогнозное значение производительности труда при увеличенном на 8% уровне механизации труда равно:

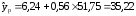усл.ед.

5. Оценка точности прогноза, расчет ошибки прогноза и его доверительного интервала.

Предельная ошибка прогноза, которая в 95% случаев не будет превышена, составит:

.

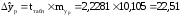Доверительный интервал прогноза.

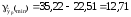
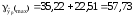
(12,71; 57,73)

6. Графическое изображение результатов и экономическое обоснование.

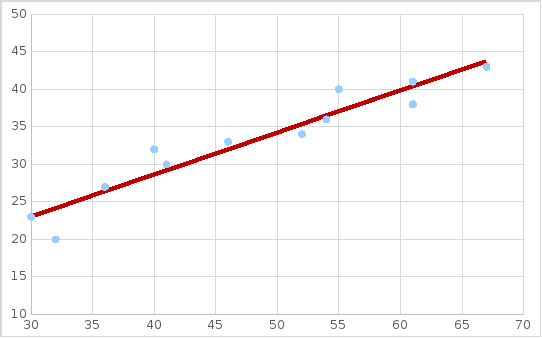
Получим уравнение парной регрессии:

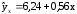
Коэффициентам уравнения линейной регрессии можно придать экономический смысл.

Коэффициент регрессии b = 0.56 показывает среднее изменение результативного показателя (в единицах измерения у) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y повышается в среднем на 0.56.

Коэффициент a = 6.24 формально показывает прогнозируемый уровень у, но только в том случае, если х=0 находится близко с выборочными значениями.

Но если х=0 находится далеко от выборочных значений х, то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо.

Подставив в уравнение регрессии соответствующие значения х, можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения.

Связь между у и х определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе - обратная). В нашем примере связь прямая.

Задача 2

Используя данные приведенные в таблице:

1. построить линейное уравнение множественной регрессии;

2. оценить значимость параметров данного уравнения и построить доверительные интервалы для каждого из параметров, оценить значимость уравнения в целом, пояснить экономический смысл полученных результатов;

3. рассчитать линейные коэффициенты частной корреляции и коэффициент множественной детерминации, сравнить их с линейными коэффициентами парной корреляции, пояснить различия между ними;

4. вычислить прогнозное значение у при уменьшении вектора х на 6% от максимального уровня, оценить ошибку прогноза и построить доверительный интервал прогноза

Номер предприятия	Прибыль, У (млн. руб.)	Выработка продукции на 1 работника Х1 (единицы)	Доля продукции производимой на экспорт Х2 (%)
1	3	13	4
2	1	9	2
3	3	12	4
4	2	11	2
5	8	18	11
6	7	15	11
7	5	13	6
8	4	12	5
9	6	15	7
10	7	16	10
11	3	9	4
12	8	18	10

Решение.

1.Уравнение множественной регрессии:

y = a₀ + a₁x₁ + a₂x₂

Матрица Х значений объясняющих переменных (матрица плана) имеет вид:

Транспонированная матрица имеет вид:

Найдем произведение матриц Х^ТХ: 

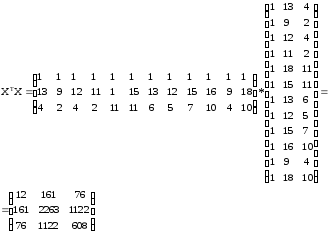
Найдем обратную матрицу:

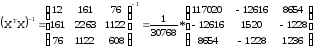
Найдем произведение матриц:

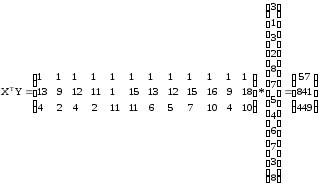
Найдем уравнение регрессии Y по Х₁, Х₂ в форме y = a₀ + a₁x₁ + a₂x₂  методом наименьших квадратов путем умножения матрицы 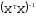 на матрицу :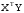

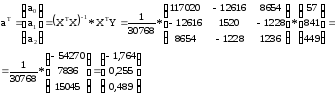
Итак: a₀ = - 1,764; a₁ = 0,255; a₂ = 0,489. 

Уравнение множественной регрессии имеет вид: 

у = - 1,764 + 0,255 x₁ + 0,489 x₂.

2.Значимость параметров уравнения множественной регрессии

Составим расчетную таблицу:

i	у	у2	у(х)	у-у(х)	(у-у(х))2
1	3	9	3,503	-0,503	0,2529
2	1	1	1,506	-0,506	0,2563
3	3	9	3,248	-0,248	0,0616
4	2	4	2,016	-0,016	0,0002
5	8	64	8,199	-0,199	0,0397
6	7	49	7,435	-0,435	0,1894
7	5	25	4,481	0,519	0,2695
8	4	16	3,737	0,263	0,0690
9	6	36	5,479	0,521	0,2712
10	7	49	7,201	-0,201	0,0403
11	3	9	2,484	0,516	0,2660
12	8	64	7,710	0,290	0,0840
Сумма	57	335	-	-	1,8002

Стандартная ошибка рассчитывается по формуле:

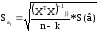
 где 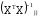 - диагональный элемент матрицы ,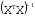  

Отсюда:

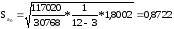
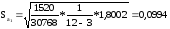
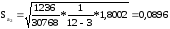
Доверительные интервалы коэффициентов регрессии рассчитываются по формуле:  a_j – t_,n-k * s_aj  а_j  a_j + t_,n-k * s_aj t_{0,95; 9} = 2,2622. Для коэффициента а₀ имеем t_{0,95; 9} * S_a0 = 2,2622 * 0.8722 = 1.973  тогда a₀ – t_{0,95; 9} * S_a0 = - 1,764 – 1,973 = - 3,737;

А₀ – t_{0,95; 9} * S_a0 = - 1,764 + 1,973 = 0,209 и доверительный интервал имеет вид (- 3,737; 0,209). Для коэффициента а₁ имеем t_{0,95; 9} * S_a1 = 2,2622 * 0,0994 = 0,225  тогда a₁ – t_{0,95; 9} * S_a1 = 0,255 – 0,225 = 0,030;

а₁ – t_{0,95; 9} * S_a1 = 0,255 + 0,225 = 0,480 и доверительный интервал имеет вид (0,030; 0,480). Для коэффициента а₂ имеем t_{0,95; 9} * S_a2 = 2,2622 * 0,0896 = 0,203  тогда a₂ – t_{0,95; 9} * S_a2 = 0,489 – 0,203 = 0,286;

а₂ – t_{0,95; 9} * S_a2 = 0,489 + 0,203 = 0,692 и доверительный интервал имеет вид (0,286; 0,692).

3.Коэффициенты корреляции и детерминации

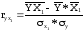
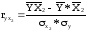
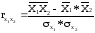
Составим расчетную таблицу:

№	х1	(х1-х1ср)2	х2	(х2-х2ср)2	у	(у-уср)2	х1у	х2у	х1х2
1	13	0,1764	4	5,4289	3	3,0625	39	12	52
2	9	19,5364	2	18,7489	1	14,0625	9	2	18
3	12	2,0164	4	5,4289	3	3,0625	36	12	48
4	11	5,8564	2	18,7489	2	7,5625	22	4	22
5	18	20,9764	11	21,8089	8	10,5625	144	88	198
6	15	2,4964	11	21,8089	7	5,0625	105	77	165
7	13	0,1764	6	0,1089	5	0,0625	65	30	78
8	12	2,0164	5	1,7689	4	0,5625	48	20	60
9	15	2,4964	7	0,4489	6	1,5625	90	42	105
10	16	6,6564	10	13,4689	7	5,0625	112	70	160
11	9	19,5364	4	5,4289	3	3,0625	27	12	36
12	18	20,9764	10	13,4689	8	10,5625	144	80	180
Сумма	161	102,9168	76	126,6668	57	64,25	841	449	1122