16. Спин: спиновые функции, спиновые операторы, разложения по спиновым функциям, сложение спинов
1.
Спин частицы равен 3/4. Какие значения
может принимать проекция ее спина на
ось 
?
а. +3/4 и –3/4 б. +3/4, 3/2, -3/2 и –3/4 в. 3/2 и –3/2 г. спин таким быть не может
2.
В результате многократных измерений,
выполненных над ансамблем тождественных
квантовых систем, были обнаружены
следующие вероятности различных проекций
спина частицы на ось 
:
,
,
.
Чему равен спин частицы?
А. 1 б. 2 в. 3 г. информации для ответа недостаточно
3. Спиновая волновая функция частицы равна
.
Чему равен спин такой частицы? а. 1 б. 3/2 в. 2 г. 5/2
4.
В каком из перечисленных состояний
частица имеет определенную проекцию
спина на ось
?
а.
б.
в.
г.
ни в одном
5.
Чему равно среднее значение проекции
спина на ось 
в состоянии 
?
а.
б.
в.
г.
6.
Какая из четырех функций ортогональна
функции 
?
а.
б.
в.
г.
7.
Частица находится в состоянии с волновой
функцией 
.
Будет ли квадрат проекции спина на ось
иметь определенное значение в этом
состоянии?
а. да б. нет в. зависит от способа измерений г. недостаточно информации
8.
Спин частицы равен ½. Чему равны
собственные значения оператора проекции
спина на ось 
?
а.
и 
б.
и 
в.
,
0 и 
г.
,
,
и 
9. Какая матрица (матрицы) отвечает эрмитовому оператору?
А.
б.
в.
г.
10. Две частицы находятся в состоянии с волновой функцией
Какие значения может принимать суммарный спин в этом состоянии?
А.
определенное значение 
б.
определенное значение 
в.
и 
с определенными вероятностями г. от 
до 
с определенными вероятностями
17. Квазиклассическое приближение
1. Квазиклассическое приближение это
а. метод перехода от квантовой механики к механике классической б. приближение, в котором оператор импульса заменяется на импульс в. метод приближенного решения стационарного уравнения Шредингера, основанный на «плавности» потенциала как функции координаты
г. метод приближенного решения временного уравнения Шредингера, основанный на «плавности» волновой функции системы как функции времени
2.
Какова размерность параметра
квазиклассичности
а.
б.
в.
г.
безразмерный
3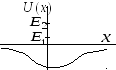
.
График потенциальной энергии частицы
имеет вид, показанный на рисунке.
Уравнение Шредингера решается при двух
энергиях -
и
(показаны на рисунке) При какой энергии
лучше работает квазиклассическое
приближение?
А.
лучше при энергии
б.
лучше при энергии
в. безразлично г. от энергии точность
квазиклассического приближения не
зависит
4
.
Решают уравнение Шредингера при энергии
в потенциалах, изображенных на рисунках
(энергия отложена черточкой на оси
потенциалов). Для какого случая можно
ожидать лучшей работы квазиклассического
приближения?
а. для левого б. для правого в. одинаково г. мало информации чтобы ответить
5.
Рассматриваем решение стационарного
уравнения Шредингера для частицы массой
в потенциале
при энергии
.
Квазиклассическое приближение
несправедливо при таких значениях
координат, которые находятся из
нижеследующего уравнения
а.
б.
в.
г.
6.
Квазиклассическое приближение работает,
если действие
,
которое имела бы частица, если бы она
двигалась по законам классической
механики, было
а.
б.
в.
г.
где
- масса частицы,
- ее энергия
7.
Из квазиклассических решений уравнения
Шредингера следует, что решение при
является:
а. растущей или затухающей функцией б. осциллирующей функцией в. постоянной
г.
зависит от
8. Для каких уровней энергии выше точность квазиклассического правила квантования
а. с маленькими квантовыми числами б. с большими квантовыми числами в. для уровней, энергия которых много больше постоянной Планка г. для уровней, энергия которых много меньше постоянной Планка
9.
Квазиклассическое правило квантования
(где
,
и
- классические точки поворота) является
уравнением, из которого можно найти
собственные значения оператора энергии.
В какие из нижеследующих величин входят
искомые собственные значения? (считать,
что график зависимости потенциальной
энергии не имеет «вертикальных» стенок)
А.
в
б.
в
и
в.
в
,
и
г.
ни в одну из перечисленных величин
10.
Чему равно значение параметра
квазиклассичности при таких значениях
координаты, где
(
- энергия, при которой решается уравнение
Шредингера в потенциале
)?
А.
0 б. 1 в.
г.
-1