Параметры некоторых эксимерных молекул

Эксимерная молекула		Длина волны в центре линии перехода, нм	Ширина полосы усиления, нм
Тип молекулы	Химическая формула
Димеры	Ar2 Kr2 Xe2	126,1 146,7 172	8 13,8 20
Галоиды	ArF KrCl KrF XeCl XeF	193,3 222 248,4 308 352,1	1,5 5 4 2,5 1,5

Используя в качестве активного элемента жидкость, можно сочетать высокую концентрацию активных частиц (как в твердом теле) с хорошей однородностью (как в газе) и возможностью непрерывной замены отработанного вещества. Это позволяет получить высокую выходную мощность при относительно небольших размерах кюветы с активным веществом.

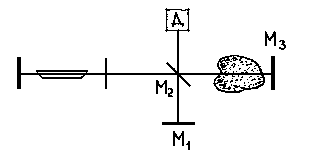
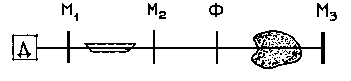
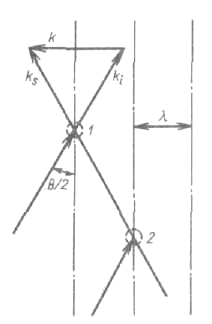
Наиболее распространены жидкостные лазеры на красителях. Красители – сложные органические соединения с полосой поглощения шириной 100-200 нм в видимой области спектра. Полосы поглощения и люминесценции определяются электронными переходами между уровнями 1 и 2 (см. рисунок). Накачка красителя осуществляется светом с частотой, попадающей в область полосы поглощения. Время жизни возбужденной молекулы красителя порядка 10^-8–10^-9 с. Для обеспечения генерации необходимо чтобы инверсия была создана за более короткое время.

В молекулах красителей имеются метастабильные состояния 3, заселение которых приводит к конкурирующему поглощению генерируемого излучения с переходом молекулы в более высокое состояние 4. Для того чтобы метастабильные уровни не успевали заселиться, время, за которое происходит накачка, должно быть меньше

τ₂₃ = 10^-3–10^-7 с.

Для создания инверсии необходима фокусировка излучения лазерной накачки, поскольку требуется высокая плотность мощности порядка 1 МВт/см². При этом необходимое охлаждение облучаемого объема красителя происходит за счет быстрой его прокачки. В максимуме полосы усиления красителя родамина-6G мощность генерации достигает 3 Вт, для других красителей она не превышает 100  200 мВт. Мощность лазеров накачки обычно 5  7 Вт. При использовании Аr и Кr лазеров диапазон длин волн лазера на красителях составляет 400  1000 нм.

Плавная перестройка длины волны излучения для одного типа красителя в пределах нескольких десятков нанометров осуществляется с помощью дисперсионных элементов внутри резонатора. Заменой красителей и источников накачки можно осуществить перестройку длины волны во всем спектральном диапазоне от УФ до ближнего ИК. Лазеры на красителях являются уникальными перестраиваемыми источниками когерентного излучения.

Плавная перестройка длины волны излучения с помощью дисперсионных элементов внутри резонатора (3) и (6)
Спектры излучения некоторых красителей:
2. – кумарин 120 5. – кумарин 102 6. – кумарин 7 9. – родамин 110	10. - родамин 6G 12. – родамин В 13. – перхлорат крезила фиолетового 14. – перхлорат нильского голубого

Лекция 6

Перейдем к рассмотрению эффектов, которые сопровождают распространение электромагнитной волны через плазму, и того, каким образом их можно использовать для определения параметров зондируемой плазмы.

Среди эффектов взаимодействия электромагнитного излучения с плазмой, которые нашли применение в диагностике, мы уже выделили: поглощение; отражение; отклонение, на градиентах концентрации; рефракция – изменение фазовой скорости распространения волны в плазме v_ф = с/n по сравнению с вакуумом или воздухом, где n = 1; изменение поляризационного состояния при наличии в плазме магнитного поля; различного характера процессы рассеяния фотонов в плазме.

Распространение зондирующей электромагнитной волны в плазме обычно описывают на основе уравнений электродинамики сплошных сред. Для поперечной волны с напряженностью , где  - частота, k=2/ - волновое число электромагнитной волны, волновое уравнение принимает вид (при divE=0):

, (6.1)

где с – скорость света, комплексная диэлектрическая проницаемость ( – диэлектрическая проницаемость,  - проводимость).

Физический смысл имеют показатель преломления n и показатель поглощения . Эти величины связаны с комплексной диэлектрической проницаемостью соотношением: . После соответствующих подстановок из (6.1) получают дисперсионное уравнение, связывающее параметры плоской поперечной волны и плазмы:

(6.2)

Длина электромагнитной волны  отличается от длины волны в вакууме ₀ и равна =₀/n, а фазовая скорость - v_ф=с/n. Таким образом, при распространении зондирующей электромагнитной волны плазма вносит в нее амплитудные, определяемые коэффициентом поглощения , и фазовые, величина которых определяется показателем преломления n, изменения.

Подставив (6.2) в выражение для волны, распространяющейся в направлении x, получим: , откуда видно, что первый сомножитель (вещественная часть выражения) определяет скорость распространения света v = с/n в среде с показателем преломления n, а мнимая часть (второй экспоненциальный сомножитель) – затухание волны в пространстве. Коэффициент поглощения α, характеризующий скорость затухания интенсивности света в среде и фигурирующий в законе Ламберта-Бера I(x) = I₀·exp(-αx), связан с показателем поглощения χ (поскольку I ~ E²) соотношением: .

При распространении электромагнитной волны в сильноионизованной, столкновительной равновесной плазме вдоль магнитного поля

, (6.3)

где - электронная плазменная частота (e и m_е - заряд и масса электрона), - эффективная частота электронных кулоновских столкновений (Z – заряд иона, Λ- кулоновский логарифм), - электронно- циклотронная частота (Н - напряженность магнитного поля). В случае слабоионизованной плазмы _эф в основном определяется частотой столкновений электронов с нейтральными частицами , где N_a – плотность нейтральных частиц сорта «а», а – размеры частиц.

В отсутствии магнитного поля и при условии пренебрежения соударениями >>_эф, выражение (3.3) упрощается и совпадает с классической формулой для электронного газа:

. (6.4)

Для интересующего нас случая оптических частот (>>_p) выполняется неравенство ()>>0 и с учетом того, что  = n², получим (после разложения в ряд и ограничившись первым членом) известную формулу:

(6.5)

При прохождении излучения через плазменный объект размером оптическая длина пути n изменится на величину:

Δ(n) = n · – = – 4,49·10^-14·λ²· (6.6)

Таким образом, измерение этого изменения, проведенное, например, методами интерферометрии, даст значение , называемой линейной плотностью (в [см^-2]).

В условиях экспериментального зала, фазовый сдвиг Δφ, измеряемый интерферометрическими методами, определяется, как изменением показателя преломления n самой плазмы размером вдоль зондирующего луча, так и изменением геометрической длины L плечей интерферометра, вызванной вибрациями оптических элементов, и может быть записан в виде:

(6.7)

Для газов при температурах менее 10⁴ К вклад в n вносят и нейтральные атомы в основном состоянии. В видимом диапазоне для большинства газов изменение показателя преломления за счет взаимодействия волны с ними можно записать в виде, известном как формула Коши :

. (6.8)

Рис. 6.1 Относительный вклад электронов и атомов в показатель преломления в зависимости от состава плазмы и длины волны зондирующего излучени

Здесь _1k и f_1,k – длина волны и сила осциллятора, соответствующие переходу между 1^ым и k–м уровнями, N_Л – число Лошмидта, N_a – концентрация атомов в нормальном состоянии. Для видимой области спектра В/²<<А, и рефракция атомов и молекул практически не зависит от длины волны. Величины А и В для различных атомов приведены в книге В.Аллена «Астрофизические величины».

Выражение (6.8) можно записать в следующем виде:

, (6.9)

где æ_а – поляризуемость и С_а  = А/N_Л – рефракция в расчете на один атом в [см³].

На рис. 6.1 представлена расчетная зависимость соотношения вкладов электронов и атомов для ряда газов (водорода, аргона, ксенона и воздуха) в показатель преломления в зависимости от длины волны зондирующего излучения в пренебрежении различием в поляризуемости атомов, ионов и возбужденных частиц. При расчете использованы параметры А и В газов находящихся в нормальных условиях (0⁰С, 760 мм. рт. ст.). В области расположенной выше линий (n − 1)_e / (n − 1)_a = 1 преобладающий вклад в величину показателя преломления плазмы вносят электроны, ниже – область, в которой показатель преломления определяется, в основном, атомами соответствующих газов.

Большéй наглядностью обладает таблица, в которой для двух газов (водорода и ксенона) и для двух длин волн излучения He-Ne лазера приведена степень ионизации плазмы (в %), при которой вклады электронов и нейтралов в показатель преломления равны.

Газ\ λ мкм	0,63	3,39
Н	3 %	0,1 %
Хе	15 %	0,5 %

Нейтральные атомы благородных газов по сравнению другими элементами таблицы Менделеева дают max относительный вклад в показатель преломления. Второй вывод: чтобы не учитывать вклад нейтралов необходимо для зондирования использовать излучение ИК-диапазона.

В общем случае, сдвиг фазы электромагнитной волны в плазме определяется как:

, (6.10)

где z₁ и z₂ – координаты границ плазмы вдоль распространения зондирующей волны.

Рассмотрим электрические свойства плазмы в зависимости от частоты. Ограничимся наиболее интересным для ТЯС случаем высокоионизованной и высокотемпературной плазмы, когда ν << ω_p. В этом случае можно выделить три области соотношений между характерными частотами (плазменной частотой ω_p, частотой кулоновских столкновений ν и частотой зондирующей волны ω):

1.	ω << ν << ωp	(6.11а)
2.	ν < ω <ωp	(6.11б)
3.	ν << ωp < ω	(6.11в)

Магнитное поле в нашем рассмотрении пока отсутствует и величиной ω_Не в (6.3) мы пренебрегаем.

Тогда в первом случае (6.11а) проводимость в основном действительная величина и описывается обычным для элементарной кинетической теории проводников выражением. Длина затухания волны, как и в металлических проводниках, напоминает скин-слой с той разницей, что в плазме с увеличением температуры проводимость увеличивается, а значит и уменьшается длина проникновения волны в плазму. Выражение для глубины проникновения δ выглядит следующим образом:

(6.11а1)

т.е. δ ~ ω^-1/2 и зависит от температуры, т.к. ν = f_(T) .

Во втором случае (средних частот зондирования) получаем, что глубина проникновения такой волны практически постоянна и соизмерима с длиной волны плазменных колебаний в свободном пространстве – δ ≈ с/ ω_p .

И, наконец, когда справедливо соотношение (6.11в), диэлектрическая проницаемость плазмы (6.3) становится положительной действительной величиной и волна распространяется в плазме почти без затухания. Для этого случая выражение для δ выглядит следующим образом:

(6.11в1)

T2 = 10 T1

Все три рассмотренных случая хорошо иллюстрируются графиком зависимости δ = f (ω/ ω_p) для двух значений температур Те, где δ выражена в единицах (с/ ω_p).

Необходимость учета влияния магнитного поля в плазме, а значит вклада электронно-циклотронной частоты в диэлектрическую проницаемость (6.3), может появиться при распространении электромагнитной волны вдоль магнитного поля. Знаки (±) перед ω_Не в выражении (6.3) для ε(ω) относятся к различным направлениям вращения круговых поляризаций, а это приводит к различию в фазовых скоростях распространения для них. Формально линейно поляризованную волну можно разложить на две волны, поляризованные по кругу. Такая волна рассматривается как суперпозиция двух волн равной амплитуды, вращающихся в противоположные стороны. Тогда, после распространения обеих волн через магнитоактивную плазму (вдоль H), на выходе из нее, из-за разных скоростей между ними появляется разность фаз. Сложение двух волн с круговой поляризацией снова даст линейно поляризованную волну, но из-за появившейся разности фаз Δφ между ними, плоскость поляризации (в которой колеблется вектор Е электромагнитной волны) повернется на угол θ = Δφ/2. Явление вращения плоскости поляризации получило название - эффект Фарадея.

Из рисунка можно понять принятые знаки, обозначения и названия для различных направлений вращения вектора поляризации:

Правополяризованной волне соответствует знак (–), направление вращения ее вектора поляризации совпадает с направлением вращения электрона в магнитном поле. Направление вращения вектора поляризации левополяризованной волны (+) совпадает с направлением вращения иона в магнитном поле.

Таким образом, измерение угла поворота плоскости поляризации может дать информацию о величине и направлении магнитного поля в плазме.

Лекция 7

Весь спектр электромагнитного излучения условно разделен на ряд частично перекрывающихся областей:

- Радиоволны. Электромагнитное излучение с длинами волн примерно от 10^-1 до 310⁴ м. Действие прибора, явившегося первым в мире приемником радиоволн, А.С.Попов продемонстрировал 7 мая 1895г на заседании Русского физико-химического общества в Петербурге.

- Микроволновое излучение. Излучение с длинами волн примерно от 0,5 мм до 30 см (частотный интервал от 0,6 до 10³ МГц). Микроволновая техника получила развитие во время Второй мировой войны в связи с необходимостью создания средств радиолокации.

- Инфракрасное излучение. ИК - излучение было открыто английским астрономом В.Гершелем в 1800 г. Инфракрасная область спектра простирается примерно от 0,8 мкм до ~ 1 мм. В ИК-диапазоне работают приборы ночного видения.

- Видимая область. Составляет ничтожно малую часть полного электромагнитного спектра, от 380 нм (фиолетовая граница) до 780 нм (красная граница), но по своему значению в жизни человека является, по понятным причинам, самой важной.

- Ультрафиолетовое излучение. УФ - спектральная область была обнаружена в 1801 г. И.Риттером и У.Волластоном, которые при исследовании солнечного спектра, наблюдали почернение хлорида серебра излучением, более коротковолновым, чем видимое фиолетовое. К УФ-диапазону относится излучение с длинами волн 185  400 нм.

- ВУФ - излучение. «Вакуумный ультрафиолет» получил свое название для длин волн короче 185 нм, т.к. поглощается воздухом и большинством прозрачных для видимого света материалов. Нижнюю его границу, которую ряд исследователей относят к мягкому рентгеновскому излучению, можно установить при 10 нм.

- Рентгеновское излучение. В 1895 г. В.Рентген обнаружил, что бумажный экран начинает светиться, если его поднести к работающей газоразрядной трубке, и сделал вывод, что свечение возникает под действием проникающего излучения, названного им X-лучами. Длинноволновая граница рентгеновского излучения перекрывается с вакуумным ультрафиолетом, а коротковолновая составляет долю нанометра. Количественно, в физике плазмы РИ принято характеризовать в энергетических единицах – кэВ. Для их перевода в длины волн используется простое соотношение 1 Å соответствует 12,4 кэВ.

- Гамма-излучение. Гамма-излучение отличается от рентгеновского еще меньшей длиной волны (большей энергией) и своим ядерным происхождением. Возбужденное ядро, возвращаясь в состояние с более низкой энергией, отдает избыточную энергию, испуская гамма-квант.

Прежде чем перейти к описанию экспериментального определения параметров плазмы напомним о физических величинах, характеризующих электромагнитное излучение, и единицах их измерения.

Радиометрия - раздел прикладной физики, занимающийся измерениями электромагнитного излучения. Принятые в радиометрии единицы измерения – система СИ. Энергия излучения измеряется в [Дж], а мощность (или поток излучения) в [Вт].

Раздел радиометрии, ограниченный измерениями в видимой области спектра, носит название – фотометрия. Световые единицы измерения связаны с реакцией человеческого глаза на излучение. В основе всего лежит мера физиологического ощущения, возникающего при попадании в глаз определенного потока излучения, или светового потока. В системе СИ основной единицей является единица силы света, отношение светового потока к телесному углу, в котором он распространяется. Единица измерения – канделла [кд] — сила света в данном направлении от источника монохроматического излучения с частотой 540∙10¹² Гц, имеющего интенсивность излучения в этом направлении равную 1 / 683 Вт в телесном угле равном одному стерадиану.

В 1931 Международная комиссия по освещению (МКО) ввела понятие «стандартного наблюдателя» как некоего среднего для людей с нормальным восприятием. Этот эталон МКО – не что иное, как таблица значений относительной световой эффективности излучения с длинами волн в диапазоне от 380 до 780 нм через каждый 1 нм. На рис. 7.1 представлен график, построенный по данным этой таблицы. Часто эту зависимость называют КРИВОЙ ВИДНОСТИ :

Рис.7.1 Кривая видности (спектральная чувствительность глаза «стандартного наблюдателя»)

Ниже приведена, взятая из учебного пособия по оптике, таблица с радиометрическими и фотометрическими единицами измерения:

Энергетические единицы измерения света				Световые единицы
	Величина	Обозначение	Единицы	Величина	Обозначение	Единицы
1	Энергия излучения	E, W	Дж	Сила света	I	кд (канделла)
2	Поток излучения	Фэ	Вт	Световой поток	Ф	лм (люмен)
3	Сила света	Iэ	Вт/ср	Световая энергия	Q, Qv	лм⋅с
4	Интенсивность излучения	S	Вт⋅м-2	Светимость	M	лм⋅м-2
5	Поверхностная плотность мощности	dФ/dS	—″—	Освещенность	E	лм⋅м-2
6	Освещенность	Eэ	—″—	Яркость	B	кд⋅м-2
7	Светимость	R	—″—	Световая экспозиция	H=ET	лк⋅с
8	Яркость	Bэ	Вт/(ср·м2)	Световая	эффективность:
9	Объемная плотность энергии	u, w	Дж/м3	Абсолютная	V=Ф/Фэ	лм/Вт
10	Экспозиция	Hэ	Дж/м2	Относительная	Kλ=Vλ/Vmax	—

На длине волны 555 нм (частота 5,4⋅10¹⁴ Гц) 1 Вт мощности излучения равен 683 лм.

Наиболее часто в научной и учебной литературе в качестве меры энергии для излучения используется термин интенсивность. Под интенсивностью различные авторы понимают такие величины как освещенность, яркость, величина светового потока и др.

Величину ν̃ = 1/ λ называют волновым числом и в лазерной физике часто используют как меру частоты или энергии фотонов. Волновое число ν̃ = 1 см^-1 соответствует излучению с длиной волны λ = 1 см, частотой 3⋅10¹⁰ Гц и энергией кванта света 1,24∙10^–4 эВ. Все эти величины — длина волны, волновое число, частота, энергия фотона однозначно между собой связаны. В разных областях физики предпочтение отдается той или иной величине. Некоторые спектральные приборы проградуированы в шкале волновых чисел, и в научной литературе эта шкала используется достаточно часто.

Зондирование плазменного объекта можно осуществлять:

- широким лазерным пучком, превышающим размеры плазмы. Тогда при регистрации прошедшего через плазму излучения необходимо визуализировать и зафиксировать все поле изображения на бумажном носителе информации, либо виртуально.

- узким лучом диаметром 1÷2 мм, мéньшим поперечных размеров плазмы. В этом случае, регистрация интенсивности прошедшего излучения (в какой-то точке с определенными координатами) выполняется с помощью фотоприемника, преобразующего его энергию в электрический сигнал. Основные типы электрических фотоприемников: фотодиоды, фотосопротивления, фотоэлектронные умножители, пироприемники, болометры и др.

Наиболее распространенным типом фотоприемников с внутренним фотоэффектом являются фотосопротивления (фоторезисторы).

Рис.7.2 Устройство фоторезистора (а) и схема его включения (б). 1 – диэлектрик, 2 – полупроводник, 3 – металлические контакты.

Фотодиод, обладающий существенно более высоким временным разрешением, представляет собой пластинку из металла, на которую нанесен тонкий слой полупроводникового материала с напыленной поверх него тонкой пленкой золота. Толщина антиокислительной пленки подобрана так, что она проводит электричество, но при этом пропускает свет. Излучение, попавшее на полупроводник, вызывает дрейф свободных электронов, которые заряжают металлическую пленку относительно него отрицательно. Режим фотодиода в отсутствие внешнего источника питания, когда полезным сигналом является фото-ЭДС, носит название фотовольтаического.

Рис. 7.3 Схемы включения фотодиода: а – фотодиодный режим; б – фотовольтаический режим.

Наибольшее применение находят германиевые и кремниевые фотодиоды. Кремниевые фотодиоды чувствительны в диапазоне 0,4÷1,2 мкм с максимумом на λ=0,8 мкм, а германиевые – в диапазоне 0,4÷2 мкм с максимумом на λ=1,5÷1,6 мкм. В области больших длин волн можно выделить фотодиоды из арсенида индия (InAs), работающие при охлаждении до 233°К и чувствительные в диапазоне 1,5÷3,6 мкм с максимумом на λ=3,3 мкм, и фотодиоды из сурьмянистого индия (InSb), работающие при температуре 77°К в диапазоне 3,0 ÷ 5,7 мкм с максимумом чувствительности на λ=5 мкм.

Приемники, чувствительные к излучению 10 мкм, расширяют возможности диагностики за счет применения газовых СО₂ – лазеров. Фотодиоды на основе тройных соединений теллуридов кадмия–ртути Hg_1-х Cd_х Te обладают высокими значениями обнаружительной способности и временного разрешения.

Лучшими характеристиками по сравнению с обычными фотодиодами обладают лавинные фотодиоды. В этих приборах при высоких обратных напряжениях, близких к пробивному, наблюдается эффект лавинного умножения фототока, вызванный тем, что неосновные носители в сильном поле p–n-перехода приобретают дополнительную энергию, достаточную для образования новых электронно-дырочных пар.

Фотодиоды, обладая весьма высокой квантовой эффективностью, достигающей 70 ÷ 80%, уступают фотоприемникам с внешним фотоэффектом ― фотоэлектронным умножителям (ФЭУ) по порогу чувствительности, поскольку в последних используется внутреннее усиление фототока, достигающее 10⁶ ÷ 10⁷ раз.

В ФЭУ для многокаскадного усиления фототока используется явление вторичной электронной эмиссии, благодаря чему эти приборы обладают высокой чувствительностью (теоретически коэффициент усиления тока может достигать значения ~ 10⁸) и служат для регистрации малых световых потоков. Принцип работы ФЭУ ясен из рис. 7.4.

Рис.7.4

Световой поток Ф вызывает фотоэмиссию с фотокатода ФК. Фотоэлектроны ускоряются к электроду Д₁ называемому динодом и выбивают с его поверхности вторичные электроны, т.к. он имеет положительный потенциал относительно катода и является вторично-электронным эмиттером. Далее вторичные электроны с динода Д₁ направляется на второй динод Д₂ и т. д. С последнего Д_n – динода электронный ток попадает на анод А.

К достоинствам ФЭУ следует отнести очень высокое быстродействие. Недостаток – необходимость источника высокого (1÷2 кВ) стабилизированного напряжения. Малые размеры таких источников достигаются за счет применения преобразования напряжения на высокой частоте ~ 10÷50 кГц.

При визуализации прошедшего через плазму излучения (регистрации изображения) с пространственной структурой (теневые изображения, интерференционные картины и т.д.) до сих пор применяются фотоматериалы, т.к. они обладают высоким пространственным разрешением, что связано с самим процессом получения изображения. Фотоэмульсия представляет собой желатин с вкрапленными в него микроскопическими (~ 1 мкм) кристалликами галогенида серебра AgBr. Когда на этот кристалл падает свет, происходит физико-химическая реакция разложения молекулы (в реакции участвует очень малая часть молекул, составляющих зерно). При этом бром сорбируется желатином, а фотолитическое серебро выпадает в виде особых образований по 1÷3 атома – центры скрытого изображения. При проявлении фотопленки реагируют все молекулы засвеченного кристаллика и образуются микронные зерна металлического Ag, а Br выводится в раствор. Таким образом, пространственное разрешение при регистрации с помощью фотоэмульсии может достигать величины ~ 1 мкм.

Фотоэлектронная регистрация позволяет управлять самим процессом. К фотоэлектронным приемникам относятся электронно-оптические преобразователи (ЭОП) и некоторые передающие телевизионные трубки (диссектор, видикон и др.). ЭОП используются как для преобразования инфракрасного, ультрафиолетового и рентгеновского изображения в видимое, так и для усиления яркости изображения, т.е. для регистрации быстропротекающих процессов (длительностью ~ 10^-13 с). Последнее возможно благодаря тому, что зафиксированное на экране ЭОП изображение сохраняется в течение некоторого времени (до нескольких секунд) из-за достаточно большого времени послесвечения. Принцип действия ЭОП можно понять из рис.7.5.

Исследуемое изображение передается на поверхность фотокатода, или, иными словами, создается определенное распределение освещенности. При этом возникающая фотоэлектронная эмиссия имеет аналогичное пространственное распределение плотности электронного тока. Под действием разности потенциалов между фотокатодом и экраном электроны фотоэмиссии ускоряются и ударяют в люминофор экрана. За счет люминесценции на поверхности экрана возникает светящееся изображение перевернутое относительно исходного. Уже более 40 лет в большинстве ЭОП’ов применяется мультищелочной фотокатод, состоящий из арсенида натрия и калия, активированных цезием. Более высокой квантовой эффективностью ~ 30% обладает арсенид-галиевый фотокатод. Но из-за высокой окислительной способности AsGa сборка ЭОП’а на его основе возможна лишь в сверхвысоковакуумных условиях.

Уменьшение габаритов и улучшение характеристик ЭОП’ов стало возможным за счет применения волоконно-оптических шайб на входе (вместо стекла) и микроканальных пластин ― для умножения и транспортировки фотоэлектронов до экрана.

Обычно, чтобы описать характеристики ЭОП используются следующие параметры:

• отношение сигнал-шум S/N;

• предельное разрешение, пар линий на 1 мм, лин/мм ;

• чувствительность фотокатода, мкА/лм ;

• коэффициент усиления, кд/м²/лк ;

• максимальная выходная яркость, кд/м² ;

• эквивалент освещения фона (EBI), лк).

Для ЭОП хорошим разрешением можно считать величину 35÷50 лин/мм.

Считывание изображения с экрана производится в большинстве случаев с помощью ПЗС-матрицы (прибор с зарядовой связью, английский эквивалент - CCD). Это устройство ─ аналоговое: электрический сигнал с каждого пикселя изображения прямо пропорционален интенсивности попадающего на него света. Матрица создается на основе светочувствительных элементов из кремния Si (секция накопления). Каждый светочувствительный элемент имеет свойство накапливать заряды, пропорционально числу попавших на него фотонов. Таким образом, за время экспозиции из секции накопления образуется двумерная матрица зарядов, пропорциональных яркости исходного изображения. Накопленные заряды первоначально переносятся в секцию хранения, а далее строка за строкой ( пиксел за пикселом ) на выход матрицы. Чем выше плотность пикселей в ПЗС-матрице, тем более высокое разрешение будет получено. В диагностике плазмы ПЗС-матрица может быть использована и для прямой регистрации изображения, когда «хватает света».

Основными параметрами, ПЗС матриц являются:

• размер в пикселях;

• физический размер в дюймах (2/3, 1/2, 1/3 и т.д.). При этом сами цифры не определяют точный размер чувствительной области, а, скорее, определяют класс прибора;

• чувствительность.

Рис. 7.6 Спектральные характеристики:

1 - чувствительности глаза человека;

2 - чувствительности AsGa фотокатода ЭОП;

3 - излучения свода ночного неба;

4 - чувствительности ПЗС матрицы фирмы SONY.

Лекция 8

Среди эффектов взаимодействия электромагнитного излучения с плазмой, которые нашли применение в диагностике, мы уже выделили: поглощение; отражение; отклонение, на градиентах концентрации; рефракция – изменение фазовой скорости распространения волны в плазме v_ф = с/n по сравнению с вакуумом или воздухом, где n = 1; изменение поляризационного состояния при наличии в плазме магнитного поля; различного характера процессы рассеяния фотонов в плазме.

Плазма при частоте зондирующего излучения ω бóльшей плазменной частоты ω_р ведет себя как диэлектрик и электромагнитная волна распространяется в плазме. Глубина проникновения в плазму, когда электронная частота ν_ei столкновений в плазме не превышает ω, составляет небольшую величину δ ≈ с/ ω_p.

На 4-ой лекции в таблице были приведены длины волн лазеров, которые нашли наиболее широкое применение при исследовании плазмы, и соответствующие им значения электронных концентраций N_e^крит, при которых электромагнитная волна не проникает в плазму. Условие ω = ω_p, при котором электронная концентрация достигает этого значения, следует из выражения 6.4 (при ω < ω_p показатель преломления n становится мнимым числом).

Значение , где [λ] = см, а [n] = см^-3 . (8.1)

Как видно из рис. 8.1, спектр поглощения одиночного осциллятора имеет форму лоренцевского контура с центром при ω_р, полушириной 2Г и амплитудой, обратно пропорциональной Г.

Рис.8.1 Спектральная зависимость вещественной и мнимой частей диэлектрической проницаемости ансамбля одиночных осцилляторов на оптических частотах.

На использовании эффекта поглощения основывается один из методов диагностики плазмы. Плазму просвечивают направленным лучом электромагнитного излучения. Если волна проходит через плазму и обнаруживается приемником, помещенным с другой стороны, то концентрация плазмы ниже критической для данного значения λ. «Запирание» сигнала означает, что концентрация плазмы выше N_e^крит.

Для большинства методов на основе активного лазерного зондирования поглощение является «мешающим» фактором. На практике, для того чтобы поглощение в плазме не влияло на интенсивность прошедшего света, максимальное значение N_e^max исследуемой плазмы должно быть в 2÷3 раза меньше N_e^крит.

На рис.8.2 для характерного для импульсной плазмы временнóго хода изменения плотности (быстрое нарастание концентрации и более медленное убывание) приведен характер интерференционных сигналов при различных абсолютных значениях N_e. Кривая (в) соответствует близкому, но не равному, значению N_e^max к N_e^крит, что приводит к уменьшению амплитуды интерференционного сигнала, и полному его исчезновению (г) во временном интервале t₁ – t₂ , когда N_e ≥ N_e^крит.

Рис.8.2 Изменение во времени - плотности (а); - сигнала интерференции: без поглощения (б); с небольшим поглощеним (в); при отсечке волны в интервале времени t1–t2 (г).

Если для длины волны зондирующего излучения концентрация плазмы достигает значения N_e^крит , то положение слоя внутри плазмы с такой плотностью можно определить по отраженному от него сигналу, измерив время между моментом генерации импульса излучения и прихода на детектор отраженного. Но для этого необходимо, чтобы, как временное разрешение регистрирующей аппаратуры, так и длительность зондирующего импульса, были существенно меньше времени распространения волны от источника до плазменного объекта и обратно.

Обе методики (по поглощению и отражению) применялись на заре термоядерных исследований, когда величины N_e в плазме были невысоки, а зондирующее излучение находилось в микроволновом диапазоне. В настоящее время они находят применение при исследовании околоземной плазмы в радио- и микроволновом диапазонах.

Явление отклонения на градиентах плотности имеет те же физические основы, что и преломление света на границе двух диэлектрических сред с разными коэффициентами преломления.

Рис.8.3.а Преломление света на границе двух диэлектрических сред с разными коэффициентами преломления m > n	Рис.8.3.б Отклонение зондирующего излучения в неоднородной плазме

Угол отклонения зондирующего луча на градиентах плотности плазмы может принимать такие значения, что ограничение на величину  сверху для данного N_e из-за этого явления будет более жестким, чем может возникнуть из-за поглощения (8.1). Так, в случае параболического профиля плотности, max угол отклонения описывается формулой Θ_max = arcsin (N_e0 /N_e^крит), где N_e0 – плотность плазмы в центре шнура. Для N_e0 = N_e^крит/3 получим значимую величину Θ_max=19,4, что сделает невозможными интерферометрические измерения еще до того, как амплитуда прошедшего сигнала начнет уменьшаться из-за эффекта поглощения.

Для визуализации оптических неоднородностей в плазме (локальных изменений показателя преломления n) применяют методы теневого и шлирен-фотографирования. При этом предполагается, что поглощением зондирующего излучения можно пренебречь, а распространение лучей в исследуемой плазме и оптических системах теневого и шлирен-фотографирования подчиняется законам геометрической оптики. Анализ получаемых оптических изображений плазмы дает качественную информацию о распределении показателя преломления n. В первую очередь, определяются координаты областей плазмы с резким изменением величины n (ударные волны, границы турбулентностей и др.) и зоны непрозрачности. Кроме того, в некоторых частных случаях возможен переход к абсолютным значениям n.

Общая схема визуализации оптической неоднородности в плазме представлена на рис.8.4. Оптическое изображение плазмы регистрируют в плоскости перпендикулярной к направлению зондирования на фотослой или двухкоординатный ПЗСдетектор. Для зондирования используется лазерный пучок с поперечным диаметром близким к размеру исследуемой области.

Рис.8.4. Схема визуализации оптической неоднородности. 1-лазерный пучок; 2-плазма; 3-оптическое изображение; 4-плоскость регистрации

Прохождение лазерного пучка через оптически неоднородную среду приводит к изменению в распространении световых лучей. Их траектории определяются принципом Ферма,  световой луч распространяется по такому пути, для прохождения которого ему требуется минимальное время. Отклонение луча от своего первоначального направления приводит к перераспределению интенсивности в зондирующем пучке, прошедшем через плазму, и изменению освещенности фотодетектора.

Теневое изображение получают при отсутствии каких-либо оптических приборов между оптической неоднородностью, освещаемой пучком света, и плоскостью регистрации. В этом случае относительные изменения освещенности экрана описываются соотношением:

(8.2)

т. е. определяются второй производной от показателя преломления, проинтегрированной по линии наблюдения.

Рис. 8.5. Оптическая схема визуализации объекта методом “светящейся точки”. О  исследуемый объект, Л1     линза, ИФ  интерференционный фильтр, Ф  фотодетектор

Оптическая схема для визуализации плазменного объекта методом “светящейся точки” представлена на рис.8.5. Излучение лазера с помощью короткофокусной линзы формируется в расходящийся пучок, проходит через плазму и регистрируется фотодетектором. Для защиты теневых фотографий от собственного излучения плазмы применяется интерференционный фильтр с максимумом пропускания на рабочей длине волны  лазерного источника.

Оценку пространственного разрешения можно получить из соотношения

, (8.3)

где   размер точечного источника света, l и h   расстояния от плоскости регистрации изображения до объекта и точечного источника, соответственно.

Длина волны лазерного излучения должна быть много меньше характерного размера оптических неоднородностей в плазме. В этом случае применимы законы геометрической оптики.

Примером практического применения теневого метода могут служить исследования процессов в канале азотного лазера проведенные с помощью этой методики. Фотографии для различных моментов времени от начала инициирования разряда приведены на рис 8.6. Хорошо видно распространение ударных фронтов, как основного разряда, так и поверхностного инициирующего и распад плазмы в центре канала.

0,4 мкс	5,6 мкс
12 мкс	56 мкс

Рис.8.6 Визуализация послепробойных процессов

в электроразрядном канале ТЕА азотного лазера

Наибольшее применение для исследования плазмы нашло явление рефракции электромагнитной волны – изменения фазовой скорости распространения волны в плазме v_ф = с/n по сравнению с вакуумом или воздухом, где n = 1. Получить информацию о величине набега фазы при распространении в плазме можно с помощью интерференции.

Явление интерференции света состоит в том, что при наложении двух световых волн происходит перераспределение световой энергии в пространстве, в результате чего в одних местах пространства возникают максимумы, а в других – минимумы интенсивности. Сложение двух плоских волновых фронтов, распространяющихся под углом друг к другу, на плоском экране даст систему чередующихся темных и светлых полос. Рассмотрим как это происходит. Пусть в какую-либо точку плоскости экрана с координатой x приходят две плоские волны, описываемые уравнениями (при совпадении направления колебаний электрического вектора):

(8.4)

При распространении волн в вакууме .

Результирующее электрическое поле равно сумме этих полей и является гармоническим колебанием в той же плоскости, с той же частотой и с амплитудой, определяемой следующим выражением:

(8.5)

Учитывая, что I = E², получаем для суммарной интенсивности:

(8.6)

где I - результирующая интенсивность света в данной точке; I₁ и I₂ - интенсивности, создаваемые каждой волной в отдельности; Δφ – разность фаз складываемых колебаний.

При этом:

(8.7)

Очевидно, что при Δφ=0 , а при I₁ = I₂ = I₀ , I_МАКС = 4I₀.

Если же разность фаз Δφ=±π, то cos Δφ = -1 , и при I₁ = I₂ = I₀ , I_МИН = 0.

Если волны до точки встречи распространяются в разных средах с показателями преломления n₁ и п₂, то оптическая разность хода Δ(nl) связана с Δφ следующим соотношением . В случае сложения некогерентных волн начальная разность фаз (φ₂ = φ₁) меняется хаотически и среднее значение cos(Δφ) равно нулю, а суммарная интенсивность равна сумме интенсивностей каждой из волн I = I₁ + I₂ .

Лекция 9

Несмотря на все разнообразие схем, собственно интерферометры, созданные за более чем вековую историю их развития, можно разделить:

– по количеству лучей, участвующих в формировании интерференционной картины, на двухлучевые и многолучевые;

– по способу регистрации фазовых сдвигов интерференционных полос на приборы с визуализацией интерференционного поля и с фотоэлектрическим смешением сигналов.

Наибольшее распространение в диагностике плазмы из двухлучевых интерферометров (рис.9.1 а) и б)) получили однопроходный интерферометр Маха—Цендера (Mach—Zehnder) и двухпроходный – Майкельсона (Michelson). В интерферометре Майкельсона один из интерферирующих пучков дважды проходит через плазму, что приводит к двукратному увеличению фазового сдвига. Его основным недостатком является связь с резонатором лазера из-за обратного отражения половины мощности генерации, что требует применения оптической развязки. Обычно для этой цели применяются поляризатор совместно с ромбом Френеля или четвертьволновой фазовой пластинкой, оптическая ось которой ориентирована под углом 45⁰ к плоскости поляризации лазерного излучения.

В двухлучевых интерферометрах осуществляется амплитудное деление исходного светового пучка на два, распространяющихся в двух пространственно разнесенных плечах: измерительном, в которое помещается исследуемая плазма, и опорном. После совмещения эти пучки формируют интерференционную картину в плоскости детектора, распределение интенсивности в которой определяется выражением:

I_Σ = I₁+I₂+2√I₁I₂^ﺍ ∙₁₂ ∙cos(Δφ). (9.1)

Здесь I₁ и I₂ – интенсивности интерферирующих пучков, _1,2 - функция их взаимной когерентности, величина которой определяется свойствами источника излучения и геометрией интерференционной схемы. При равенстве интенсивностей I₁ = I₂ = I₀ и _1,2 =1, выражение (9.1) имеет более простой вид I_Σ = 4 I₀ cos² (Δφ/2).

	Тип интерферометра	Оптическая схема
а)	Маха - Цендера
б)	Майкельсона

Рис.9.1 Двухлучевые интерферометры в диагностике плазмы.

Количество полос интерференции на единицу интерференционного поля _пр (пространственная частота) определяется углом  между интерферирующими лучами и длиной волны :

, (9.2)

где d – расстояние между максимумами двух соседних полос. Результирующая интерференционная картина будет наблюдаться на фоне регулярной системы равноотстоящих друг от друга параллельных полос (полосы конечной ширины). В этом случае, если размеры интерференционного поля превышают размеры фазового объекта, то неоднородности в объекте проявляются в виде искривления опорной системы полос.

В случае, когда =0 (режим бесконечно широкой полосы), результирующая интерференционная картина представляет собой единственную полосу, уровень равномерной засветки которой зависит от Δφ интерферирующих волн. При таком способе настройки изменения в объекте проявятся в появлении замкнутых интерференционных полос, как оконтуривающих неоднородность, так и находящихся внутри нее. Однако расшифровать такую интерференционную картину можно только зная a priori знак изменения набега фазы при переходе от одной полосы к другой.

Если теперь в измерительном плече поместить плазменный объект, показатель преломления n которого отличается от первоначального показателя преломления среды n₀ (для воздуха и вакуума n₀  1), то оптическая длина пути nL, проходимого светом в измерительном плече, изменится на величину

. (9.3)

В результате между интерферирующими лучами появится дополнительная разность фаз , которая приведет к смещению интерференционных полос. Интерферометрические измерения сдвигов полос относительно их положения в отсутствие плазмы дают информацию только о среднем значении показателя преломления вдоль направления зондирования плазмы.

При работе с плазмой низкой плотности требуется измерять изменение интенсивности при смещении интерференционной полосы в пределах одного максимума аппаратной функции интерферометра от I_min до I_max (рис.9.2).

Такие измерения требуют предварительной градуировки интерферометра (измерения диапазона изменения интенсивности между минимумом и максимумом, что соответствует изменению фазового сдвига на ) и определения положения рабочей точки (начальной разности фаз относительно максимума аппаратной функции интерферометра).

Рис. 9.2 Аппаратная функция двух- лучевого интерферометра и принцип измерения малых фазовых сдвигов

Минимальная измеряемая концентрация плазмы соответствует такому смещению интерференционной полосы, которое еще может быть зарегистрировано. Чувстви-тельность двухлучевых интерферометров, т. е. отношение относительного изменения интен-сивности в полосе dI/(I_max – I_min) (dI – абсолютное изменение интен-сивности), к изменению (сдвигу, набегу) фазы за счет плазмы, вызвавшей это изменение, находится из (9.1).

Дифференциальная чувствительность интерферометра имеет максимум при =/2, что соответствует значению интенсивности, равной (I_max + I_min)/2. Соответственно, максимальная чувствительность измерения величины изменения оптической толщины двухлучевыми интерферометрами при работе в максимуме крутизны аппаратной функции в окрестности =/2 (рис.9.2) на ее линейном участке определяется минимально регистрируемой относительной величиной изменения интенсивности:

. (9.4)

Обычно для настройки на максимум крутизны аппаратной функции одно из зеркал интерферометра устанавливают на пьезоэлектрическом сдвигателе, что позволяет управлять положением рабочей точки интерферометра.

Одно- и двухпроходные интерферометры обладают нелинейной характеристикой. Было предложено проводить во время измерения непрерывную калибровку периодическим изменением длины опорного плеча интерферометра Маха-Цендера. В качестве модулятора, чтобы не потерять во временном разрешении, был применен электрооптический кристалл.

В интерферометре Маха-Цендера существенно повысить точность измерений малых фазовых сдвигов можно при фотоэлектрической регистрации интерференционного сигнала двумя фотодетекторами, включенными в дифференциальную схему. Эти сигналы сдвинуты по фазе на . Если в первом канале сигнал с детектора имеет вид U₁(t)=U_Scos(Δφ(t))+ U_N(t), во втором канале U₂(t) = – U_S·cos(Δφ(t))+U_N(t), (здесь U_S – полезный фотоэлектрический сигнал, U_N – аддитивные шумы различной природы), то после дифференциального усилителя полезный сигнал оказывается вдвое больше, чем у одиночного фотоприемника: U_(t) = U₁(t) –U₂(t) = 2U_S·cos(Δφ(t)),. В то же время одинаковое для обоих детекторов изменение интенсивности, вызванное излучением плазмы, флуктуациями мощности лазера, ослаблением лазерного излучения или изменением ширины интерференционной полосы из-за отклонения световых лучей, а также возможные электромагнитные помехи, вычитаются. Применение подобной схемы и системы активной стабилизации вибраций позволило обеспечить чувствительность на уровне 10^-4 интерференционной полосы. Для He – Ne лазера (=0.633 мкм) минимально регистрируемая N_e в экспериментах с импульсной аргоновой струей составила ~210¹³см^-3.

Из (6.6 и 9.4) следует, что верхний предел измерений возрастает с уменьшением длины волны зондирующего излучения, в то же время, чувствительность измерений растет при переходе в более длинноволновый спектральный диапазон. Однако на практике часто оказывается, что низкая эффективность технических средств регистрации излучения в дальнем ИК – диапазоне: малая спектральная чувствительность, высокий уровень тепловых шумов и т. д., приводит к необходимости перехода в видимый и ближний ИК – диапазон спектра. Вследствие более высокого отношения сигнала к шуму систем регистрации при измерениях малых изменений интенсивности интерференционного поля в видимой области, такой переход может дать выигрыш в минимально регистрируемой величине электронной плотности плазмы.

Возможности лазерной диагностической аппаратуры значительно расширяются при объединении лазера с оптическим интерферометром. Выбор же сдвигового интерферометра обеспечивает регулирование чувствительности измерений, компактность конструкции и позволяет размещать оптический прибор за пределами исследовательской камеры с плазмой.

Принцип действия интерферометра сдвига заключается в следующем. Пусть зондирующее излучение с длиной волны  направлено вдоль оси z и проходит через плазму с показателем преломления n (x, y, z), помещенную в одно из плеч интерферометра МахаЦендера. Дополнительный набег фазы

 (x, y) = 2 k (x, y)

(9.5)

приводит к смещению полос на интерферограмме. Если же зондирующее излучение проходит через изучаемую плазму до входа в интерферометр МахаЦендера, то полосы не искажаются, поскольку фазовые соотношения интерферирующих лучей не меняются по всему полю интерференции. Предположим, что с помощью интерферометра осуществлен параллельный сдвиг одного из интерферирующих пучков на величину s перпендикулярно оси z (рис.9.3). Направление сдвига может быть произвольным, но как будет показано ниже, для упрощения обработки интерферограмм удобно сдвиг осуществлять в направлении полос (пусть это будет направление вдоль оси x). В этом случае смещение интерференционных полос оказывается связанным с показателем преломления n (x, y, z) и величиной сдвига s соотношением

(9.6)

Подобная схема интерферометра была впервые предложена Бейтсом и предназначалась для измерения асферичности сходящихся пучков. Сущность этого метода состоит в том, что искаженный фронт сравнивается не с опорным (неискаженным) фронтом, а с аналогичным искаженным фронтом, но смещенным в поперечном направлении на величину s. Это означает, что в данном случае происходит интерференция пучков света, прошедших через соседние слои исследуемого объекта.

Рис.9.3. Зондирование плазмы, обладающей цилиндрической симметрией (направление зондирования совпадает с осью z, сдвиг по оси x)

Интерферометр бокового сдвига удобен при исследовании плазмы, обладающей цилиндрической симметрией (например, разряды типа Z  пинч). Просвечивание объекта осуществляется в направлении, перпендикулярном оси симметрии, а интерференционные полосы ориентируют в направлении изменения показателя преломления плазмы. Произвольные искажения волнового фронта приводят как к положительным, так и к отрицательным разностям фаз  (x, y). Соответственно и смещение интерференционных полос также изменяется как по величине m (x, y)  =   (x, y)  2, так и по направлению вдоль оси y. Вид получаемых интерферограмм и алгоритм их обработки в значительной степени зависит и от настройки интерферометра, т.е. выбора направления и величины s сдвига. Это связано с тем, что экспериментально регистрируемое смещение полос определяется разностью фазовых набегов  (x, y)  =   (x, y)   (x  s_x, y s_y),

из которой впоследствии восстанавливается функции  (x, y). Вопрос интерпретации смещения полос в сдвиговом интерферометре сложен, но достаточно проработан. Численная обработка интерферограмм упрощается при введении сдвига вдоль интерференционных полос ( направление вдоль оси x на рис 9.3 ), т.е. при s = s_x.

В зависимости от величины s возможны следующие предельные случаи:

1.Большой сдвиг (s L), где L  размер плазменной неоднородности. В этом случае интерферометр бокового сдвига вырождается в обычный интерферометр Маха-Цандера, но с двойным фазовым изображением объекта. Чувствительность измерений в этом случае максимальна.

2.Малый сдвиг (s L), где L = x₂ x₁, x₁ и x₂  границы плазменной неоднородности. Очевидно, что функция  (x) в этом случае равна

 (x) = 0          при  x   x₁    и    x  x₂

 (x) =  (x)    при  x₁   x   x₁ + s.

В интервале   x₁ + s  x    x₂ функция  (x) строится по рекуррентной формуле с шагом, меньшим или равным s

 (xi) =  (xi) +   (xi  s)

(9.7)

3. Сдвиг много меньше размера плазменной неоднородности (s L).

 (x) =  (x)   (x s) =  = x(x)s .

(9.8)

Несмотря на более сложную процедуру обработки интерферограмм, следует отметить возможность регулирования чувствительности измерений с помощью изменения величины s, что является несомненным достоинством сдвиговых интерферометров и обеспечивает исследование плазменных объектов с большими градиентами электронной плотности. Конструктивная развязка от исследуемого объекта позволяет значительно уменьшить размеры интерферометра и увеличить его устойчивость к вибрациям.

Для практического применения удобен случай, соответствующий малой величине сдвига s  R.

Лекция 10

Как следует из (9.4), для повышения чувствительности измерений малых сдвигов интерференционных полос необходимо повысить крутизну аппаратной функции интерферометра. Это может быть достигнуто использованием пассивных многолучевых интерферометров типа Фабри – Перо (ИФП) или кольцевого резонатора (рис. 10.1 в) ÷ е)). В многолучевых интерферометрах ширина максимумов интерференции  существенно меньше расстояния между ними, что позволяет измерять фазовый сдвиг с более высокой точностью по сравнению с двухлучевыми схемами (рис. 9.1).

в)	Четырехзеркальный с пассивным резонатором Фабри - Перо
г)	Эшби - Джефкотта
д)	Жерардо - Вердейена
е)	Кольцевой резонатор
Рис. 10.1 Оптические схемы классических многолучевых ( в, г, д, е ) интерферометров

Многолучевой интерферометр Фабри — Перо состоит из двух стеклянных или кварцевых пластинок М₃ и М₄ (рис.10.1в), на обращённые друг к другу и параллельные поверхности которых нанесены зеркальные покрытия с высоким (85—98%) коэффициентом отражения. Параллельный пучок когерентного света, падающий на ИФП под небольшим углом, в результате многократных отражений от зеркал образует большое число параллельных, когерентных лучей с постоянной разностью хода, зависящей от величины угла падения. Интерференционная картина представляет собой равномерно освещенное поле, интенсивность которого зависит от расстояния между зеркалами. Чтобы получить «полосы равного наклона» надо использовать расходящийся пучок света. При освещении параллельным пучком света для получения интерференционных полос «равной толщины» необходимо слегка разъюстировать зеркала.

В интерферометрах типа Фабри – Перо, использующихся в диагностике плазмы, обычно размеры зеркал малы по сравнению с расстоянием между ними, поэтому на поперечное распределение поля существенное влияние оказывают дифракционные потери электромагнитных волн на краях зеркал. По этой причине однородность волн в интерферометре нарушается, и возникают условия для возбуждения колебаний со сложной поперечной структурой. Поэтому при работе с такими интерференционными системами необходимо согласование волнового фронта лазерного излучения с интерферометром. В случае одной основной (аксиальной) моды согласование эквивалентно тому, что резонатор лазера и пассивный интерферометр имеют общую оптическую ось, а изображение перетяжки гауссова пучка лазера совмещено с перетяжкой основной моды резонатора интерферометра.

Интерференционная картина в многолучевом интерферометре формируется за счет когерентного сложения большого числа лучей при многократном отражении от зеркал интерферометра, имеющих высокий коэффициент отражения. Распределение интенсивности в проходящем свете в зависимости от разности фаз интерферирующих лучей  имеет вид (функция Эйри):

, (10.1)

где I₀ – интенсивность падающего на интерферометр света,  - приведенный амплитудный коэффициент отражения зеркал интерферометра ( ₁₂^.

Рис.10.2 Кривая пропускания интерферометра Фабри-Перо R – коэффициент отражения.

Отношение интенсивности в максимумах и минимумах, характеризующее контрастность интерференционных полос, как видно из формулы для интенсивности прошедшей волны, определяется коэффициентом отражения: Imax/Imin=(1+R)2/(1-R)2.

Многолучевая интерференционная картина в прошедшем свете при значениях R, близких к единице, имеет вид узких светлых полос на почти совершенно темном фоне.

Крутизна аппаратной функции (функции пропускания), определяется эффективным числом лучей участвующих в интерференции, т.е. числом проходов волны внутри интерферометра . Ширина интерференционной полосы, выраженная в долях разности фаз, определяется коэффициентами отражения зеркал   {1)  ^}.

Чувствительность многолучевого интерферометра определяется дифференцированием (10.1) по . В точке с максимальной крутизной аппаратной функции I  0.5 (I_max+I_min) :

. (10.2а)

Соответственно чувствительность по отношению к изменению оптической длины в плазме имеет вид:

Δφ. (10.2б)

Из сравнения (9.4) и (10.2б) видно, что многолучевые интерферометры позволяют зарегистрировать изменение оптической толщины плазмы в раз мéньшее, чем двухлучевые (рис. 9.2).

Рис. 10.3 Сравнение аппаратных функций многолучевого интерферометра (а) при =0.9 и двухлучевого Маха-Цендера (b) ( - приведенный амплитудный коэффициент отражения зеркал интерферометра ( ₁₂^) Рисунок представлен в 2-ух масштабах.

Временнóе разрешение интерферометров определяется временем формирования интерференционной картины. Если в двухлучевых интерферометрах быстродействие по существу ограничено линейными размерами установки и равно времени одного (в интерферометре Маха-Цендера) прохода излучения в измерительном плече, то в многолучевых интерферометрах временное разрешение в N_эф раз хуже.

Использование многолучевых интерферометров в диагностике плазмы в некоторых случаях может быть ограничено тем, что за счет поглощения зондирующего излучения плазмой или деградации поверхности зеркал эффективное число проходов волны внутри резонатора N_эф оказывается небольшим. Это приводит к существенному уменьшению крутизны аппаратной функции, по сути, приближая ее к двухлучевым схемам.

Представленные на рис.10.1 схемы многолучевых интерферометров на основе эталона Фабри-Перо можно считать классическими. В 1963 г. появилось в печати сразу три работы с описанием диагностических устройств, основой которых служили лазер и интерферометр, чьим прообразом являлся эталон Фабри-Перо.

В четырехзеркальном интерферометре (рис.10.1 в) резонатор лазера М₁М₂ и пассивного интерферометра Фабри-Перо М₃М₄ оптически развязаны, аналогично тому, как это описано для интерферометра Майкельсона. Плазма помещается между плоскими зеркалами М₃М₄ и изменяет оптическую длину интерферометра Фабри-Перо, фотоприемник Д регистрирует изменение интенсивности прошедшего лазерного излучения.

В 3^х зеркальных интерферометрах Эшби и Джефкотта и Жерардо и Вердейена, изображенных на рис.10.1 г), д) , соответственно, лазер используется как осветитель и как часть детектора. В этих интерферометрах резонатор М₃М₂ с помещенной в него плазмой выполняет роль зеркала лазера с переменным коэффициентом отражения, зависящим от плотности плазмы и расстояния между М₂ и М₃, что приводит к амплитудной модуляции излучения лазера, выходящего через зеркало М₁. Расстояние между модуляционными максимумами соответствует набегу фазы  = 2.

В интерферометре Эшби-Джефкотта использовался He-Ne лазер, генерировавший сразу две длины волны ₁ = 3,39 мкм и ₂ = 0,633 мкм c общим верхним уровнем для этих переходов. Это дало возможность проводить измерения на большей длине волны: в интерферометр М₂М₃ фильтр Ф (рис. 10.1 г) пропускал только ₁, модуляция же наблюдалась на более удобной для регистрации длине волны ₂ (в этом случае в качестве фотодетектора Д можно использовать ФЭУ).

Добавление к основному резонатору лазера, состоящему из сферического М₁ и плоского М₂ зеркал, еще одного глухого плоского зеркала М₃ приводит к образованию добавочного резонатора на зеркалах М₂-М₃ типа ИФП, связанного с основным. Коэффициент отражения добавочного резонатора сильно зависит от его оптической длины и влияет на интенсивность генерации лазерного излучения. С изменением оптической длины дополнительного резонатора (например, при введении в него плазмы) происходит изменение фазы отраженного этим резонатором М₃-М₂ в основной резонатор М₂-М₁ лазерного сигнала. В результате лазерное излучение, выходящее через сферическое зеркало М₁, модулируется по амплитуде. Одному периоду модуляции соответствует изменение оптической разности хода на половину длины волны лазерного излучения.

По сути, чувствительность такого интерферометра определяется теми же факторами, что и 4^х зеркального интерферометра, но временное разрешение будет связано уже с временем установления стационарного уровня излучения для ₂, которое, из-за необходимости применения высокодобротных резонаторов для ₂, достаточно велико ( 10^-6 сек).

Если же зеркало М₃ сделать сферическим (рис. 10.1 д), (при использовании сильного лазерного перехода), то в резонаторе М₂М₃ будут возникать не только аксиальные моды, но и поперечные, а это в свою очередь приведет к уменьшению расстояния между модуляционными пиками в k раз по сравнению с резонатором с плоским зеркалом М₃. Минимально измеряемая с помощью интерферометра Жерардо-Вердейена N_el будет в k раз ниже , где d₂₃ – расстояние между М₂ и М₃, а R₃ – радиус кривизны зеркала М₃.

Таким образом, лазерные интерферометры, основой которых является интерферометр типа Фабри-Перо, обладают более высокой чувствительностью, чем рассмотренные ранее одно- и двухпроходные. Тем не менее, число оптических элементов в них, так или иначе влияющих на интерференционную картину, не менее трех, что затрудняет обеспечение виброзащищенности. Кроме того, возникающая в процессе проведения эксперимента необходимость в улучшении (пусть даже ценой другого) одного из основных параметров: чувствительности, пространственного или временного разрешения, может быть реализована только переходом на другую оптическую схему, изменением количества и качества зеркал, способа регистрации и т.д.

Лекция 11

По способу регистрации фазовых сдвигов интерференционных полос интерферометры делятся на приборы с визуализацией интерференционного поля и с фотоэлектрическим смешением сигналов.

При визуализации интерференционного поля проводится измерение смещения (или искривления) интерференционных полос, вызванного появлением в рабочем поле интерферометра исследуемой плазмы. Для этого на экран проецируется некоторая плоскость разрядной камеры, обеспечивая однозначное соответствие между точками исследуемой плазмы и интерференционного поля. Достоинством этого метода является возможность получения пространственного распределения профиля показателя преломления плазмы за один импульс лазерного излучения; недостатком  необходимость (из-за больших размеров светового поля) программированного отступления от "плоскостности" при изготовлении окон вакуумной камеры для компенсации деформаций, вызванных перепадом давлений. Кроме того, при большой апертуре рабочего поля возникает необходимость в подавлении собственного излучения плазмы. При использовании ахроматической линзы диаметром 260 мм и установленной в ее фокальной плоскости диафрагмы диаметром 0.4 мм, по утверждению авторов этой работы, удалось ослабить излучение плазмы в 410⁵ раз. Использование фоторегистраторов на основе приборов с зарядовой связью (ПЗС), сопряженных с компьютерами, позволяет привлечь для обработки двухмерных интерференционных картин цифровые алгоритмы обработки и анализа изображений и существенно повысить точность измерений.

При регистрации на фотоэмульсию точность измерения малых плотностей плазмы (когда   0,5) ограничивается погрешностью микрофотометрирования интерферограмм. При использовании двухлучевого интерферометра минимально регистрируемый фазовый сдвиг составит величину  _min  210^-2  рад, что для зондирующего излучения   0,63 мкм, дает предельно измеримую электронную плотность (N_e)_min  10¹⁵ см^-3.

Фотоэлектрическое смешение световых полей на фотоприемнике с квадратичной характеристикой обладает более высокими метрологическими характеристиками по сравнению с визуализацией интерференционного поля. Фотоэлектрическое смешение может применяться с интерферометрами любых типов и практически не имеет ограничений на спектральный диапазон зондирующего излучения. Так, ряд технических решений в интерферометрии оптического диапазона с фотоэлектрическим смешением были напрямую перенесены из СВЧ интерферометрии.

Точность измерения малых фазовых сдвигов ( / 2 << 1) при фотоэлектрическом смешении по существу ограничивается флуктуациями амплитуды и частоты зондирующего излучения и шумами фотоприемного устройства. При отношении сигнал/шум равным единице поток излучения [Вт], приходящийся на единицу полосы пропускания фотоприемного устройства [Гц] (обусловленной его амплитудно-частотной характеристикой) и падающий на поверхность приемника площадью S_d [см²], называется эквивалентной мощностью шума приемника Q_ [ВтГц^-1/2]. Величина Q_ для приемников света, работающих в УФ  и видимом диапазонах спектра порядка (10^-15–10^-17) ВтГц^-1/2, в инфракрасной области (10^-12–10^-15) ВтГц^-1/2.

В области нескольких кГц и ниже избыточный, по отношению к уровню естественных, шум известен как фликкер-шум, или шум ~1/f, поскольку его спектральная плотность примерно обратно пропорциональна частоте. Природа фликкер-шума сложна и в основном определяется типом используемого фотодетектора и особенностями его конструкции.

В большинстве случаев основное ограничение на чувствительность фотоэлектрического измерения фазового сдвига вносят флуктуации в генерации лазера. Флуктуации в лазерах принято разделять на технические и естественные. Технические флуктуации обусловлены нестабильностью параметров резонатора и накачки активной среды лазера. Спектральная ширина технических шумов не более ~10⁴ Гц. В газовых лазерах дополнительным источником технических флуктуаций излучения являются возмущения плазмы разряда с шириной спектра до 10⁶ Гц. Принципиально неустранимый квантовый предел шумов  это спонтанный шум активной среды, который приводит к флуктуациям частоты и мощности генерации лазера [129]. Для одночастотных лазеров ширина спектра естественных шумов мощности ограничена шириной полосы пропускания резонатора =_л/Q, где _л – частота генерации лазера, Q – добротность резонатора. Так для He-Ne лазера на переходе, соответствующем длине волны 0.63 мкм, генерация возможна только при использовании высокодобротного резонатора с полосой ~1 МГц, в то же время для  = 3.39 мкм полоса резонатора может превышать 100 МГц.

Если при визуализации интерференционного поля обработка интерферограммы позволяет восстановить пространственное распределение электронной плотности для определенного момента времени, то при фотоэлектрической регистрации восстановить профиль электронной концентрации возможно только при многоканальном просвечивании плазмы.

Практика использования лазерных интерферометров показывает, что всегда присутствующие в условиях экспериментального зала шумы и вибрации могут серьезно затруднить проведение измерений. Необходимо искать пути защиты от «паразитных» флуктуаций самого диагностического прибора. Простая оценка для λ = 3,39 мкм показывает, что при необходимости исследовать плазму с N_e ≈ 10¹² см^-3 изменение длины резонатора за время измерения (~100 мксек), равное по амплитуде полезному сигналу, может быть вызвано внешними возмущениями оптической длины резонатора лазера с частотой 50 Гц и амплитудой всего 0,2 мкм. Неудобство в работе, особенно при настройке и калибровке, вызывает медленное изменение длины резонатора (тепловой дрейф), вызванное колебаниями температуры окружающего воздуха.

Без создания автономного прибора, элементы которого механически не связаны с вакуумной камерой, воспринимающей вибрации здания в целом и от находящегося неподалеку вспомогательного оборудования, проводить диагностику в условиях экспериментального зала крайне трудно.

Наиболее приемлемым вариантом виброизоляции интерферометра, по-крайней мере для диагностики плазмы на научных экспериментальных установках, является применение амортизирующей подвески станины с закрепленными на ней элементами интерферометра.

Разработанная в МИФИ подвеска станины состояла из амортизирующих резиновых жгутов, которые крепились к потолку через «слоеную» амортизирующую прокладку, состоящую из микропористой резины и свинца. Основной виброизолирующий эффект был получен с помощью жгутов, но заметный вклад, примерно в 2–3 раза, дала тщательно подобранная многослойная система прокладок.

Наилучшие результаты были получены с помощью жгутов с площадью сечения s=1см², применяемых для запуска планеров с земли. Они выполнены из пучка резиновых «нитей», помещенных под нагрузкой в оплетку из плотной ткани, так что они постоянно находятся при относительном удлинении Δl/l₀ ≈ 0,4. Относительное удлинение ≈ 0,7, когда наиболее полно проявляются амортизирующие свойства жгутов, достигается под действием массы m ≈ 15 кг (F ≈ 150 Н). Поэтому при выборе количества жгутов необходимо исходить из того, что нагрузка на каждый из них должна находиться в пределах (150 – 250) H.

Но даже грамотно сконструированной, пассивной системы защиты от внешних возмущений оказывается недостаточно. Создание системы, позволяющей поддерживать геометрическую длину резонатора неизменной во время измерений и в предпусковой период, является одним из самых важных моментов в успешном использовании лазерных диагностических интерферометров видимого и ближнего инфракрасного диапазона.

Положительный результат был получен при анализе работы системы стабилизации в терминах и методами теории автоматического регулирования.

Рис.11.1 Электрическая принципиальная схема активной стабилизации интерферометра, его калибровки и получения полезного сигнала

На рис. 11.1 приведена электрическая схема включения системы стабилизации и калибровки интерферометра типа КРИОП. Система стабилизации включала минимальный набор элементов (что позволяло более четко выявить влияние параметров каждого из них на работу в целом): фотодетектор ФП₂ с коэффициентом преобразования К_Д излучения лазера в электрический сигнал в (Вт/В); усилитель У, в качестве которого мог использоваться осциллограф С1-19, с коэффициентом усиления К_ус; корректирующее звено КЗ, коэффициент передачи которого К_кз – комплексное число; регулирующий элемент ПК₂, в качестве которого испытывались различные типы пьезокорректоров с коэффициентом преобразования электрического сигнала в линейное перемещение К_пк в (В/м) и сам лазерный излучатель, преобразующий изменение длины резонатора в изменение интенсивности излучения с коэффициентом К_ЛАЗ (м/Вт). В нашем случае правомерно и целесообразно ввести новый коэффициент преобразования линейного перемещения в электрический сигнал К_фп = К_ЛАЗ  К_ФД. Сигнал на экране осциллографа после калибровки легко перевести в перемещение.

В теории автоматического управления каждое звено характеризуется своей передаточной функцией равной отношению сигнала на выходе звена к сигналу на входе. Передаточные функции могут быть размерными К_ФП, К_ПК и безразмерными К_УС, К_КЗ, действительными числами К_УС, К_ФП и имеющими мнимую часть К_КЗ, К_ПК.

Появление мнимой части связано с инерционностью звена, то есть наличием сдвига фаз между выходными и входными сигналами. Вся система характеризуется передаточной функцией разомкнутой системы W_P(j), которая равна произведению передаточных функций отдельных звеньев:

(11.1)

Пусть колебания резонатора под действием внешних возмущений описываются зависимостью , а после включения системы стабилизации их амплитуда уменшится до , тогда .

Отношение сигналов при включенной и отключенной системе обратной связи есть передаточная функция по динамической ошибке F, которая имеет вид:

(11.2)

Представляя в общем виде и сделав несложные преобразования получаем:

(11.3)

здесь и – амплитудная и фазовая, соответственно, частотные функции. Изображенные графически в зависимости от частоты, они будут называться амплитудночастотная характеристика (АЧХ) и фазочастотная характеристика (ФЧХ).

Из выражения (11.3) следует: 1) Эффект стабилизации будет проявляться, в той или иной мере (то есть система будет устойчива) всегда при , так как в этом случае. Система становится неустойчивой (наступает раскачка колебаний) вблизи резонанса колебательной системы. Поэтому рабочий диапазон системы стабилизации находится вдали от резонансов. 2) Эффективно система стабилизации будет работать только если. Это условие также накладывает ограничение на рабочий диапазон системы.

Изображенная на рис.11.1 система активной стабилизации, основанная на разработанных нами и изложенных выше принципах функционирования, хорошо отрабатывает такие внешние возмущения длины интерферометра, когда характерные частоты изменения параметров импульсной плазмы лежат за пределами динамического диапазона этой системы. В случае нарушения этих условий система не различает причины вызвавшие изменения оптической длины резонатора. В этом случае при построении активной системы защиты от внешних возмущений необходимо использовать дисперсионные свойства плазмы.

Использование двухволновых интерферометров с сильно различающимися длинами волн является наиболее универсальным методом, позволяющим выделить малое изменение электронной плотности плазмы на фоне сильных вибраций и применимый для широкого класса плазменных установок и параметров плазмы.

При проведении интерферометрических измерений на двух длинах волн фазовые сдвиги Δφ, за счет вклада показателя преломления плазмы и изменения геометрической длины L плечей интерферометра на величину L из-за вибраций оптических элементов, имеют вид:

(11.4)

Решая эту систему уравнений можно из суммарного фазового сдвига выделить составляющую, вносимую электронной компонентой плазмы

. (11.5)

Другим вариантом двухволновой интерферометрии является использование меньшей длины волны ₁ в системе стабилизации интерферометра работающего на длине волны ₂ (₁<₂). Действительно в этом случае левая часть первого уравнения системы (11.4) с определенной точностью будет равна нулю и 2-е уравнение можно представить в виде:

(11.6)

Такой подход был применен при создании прибора для диагностики на установке Т - 9 в ИАЭ им.И.В.Курчатова.

На рис.11.2 приведены осциллограммы иллюстрирующие эффективность работы системы стабилизации (момент ее включения отмечен стрелкой).

Лекция 12

Электрооптические кристаллы (ЭОК) нашли широкое применение в лазерной технике. В диагностической аппаратуре на основе лазеров они используются для модуляции частоты, для сдвига частоты и даже в системе стабилизации величины выходной мощности лазерного осветителя.

Для модуляции оптической длины фазоанизотропного резонатора лазерного интерферометра, помещенный внутрь резонатора ЭОК при приложении к нему электрического поля должен изменять длину оптического пути (для каждой из взаимноортогоналъных мод на одну и ту же величину), не внося при этом в резонатор дополнительной анизотропии. В главной системе координат эллипсоид показателей преломления имеет вид:

(12.1)

где a_ij - поляризационные константы, ось Z совпадает с направлением оптической оси.

Кристалл ниобата лития (LiNbO₃) обладает линейным злектрооптическим эффектом, а это значит, что приращение поляризационных констант при приложении электрического поля выражается следующим образом:

(12.2)

где r_i - коэффициент линейного злектрооптического эффекта (индекс i принимает значения от 1 до 6).

Для LiNbO₃ значения отличные от нуля имеют следующие коэффициенты:

; ; ;

(12.3)

При приложении электрического поля {Е_X, Е_Y, Е_Z} эллипсоид показателей преломления, вообще говоря, примет вид:

(12.4)

Если поле совпадает с оптической осью кристалла () и направлением излучения лазера, то уравнение (12.4) примет простой вид:

(12.5)

Отсюда, по определению, показатели преломления для каждой из поляризаций (для обыкновенного n_o’ и необыкновенного n_e’ лучей) равны по величине:

(12.6)

При размещении таким образом ориентированного кристалла внутрь резонатора двухмодового лазерного интерферометра при изменении величины Е изменится его оптическая длина на величину:

(12.7)

где l - длина кристалла вдоль оптической оси, U - прикладываемое напряжение.

В гетеродинном интерферометре (рис.3.5) для повышения чувствительности измерений применяется перенос информации на промежуточную частоту и его можно отнести к широкому классу диагностических приборов - интерферометрам с преобразованием частоты. В основе большинства из них лежит гомодинное преобразование частоты.

Если излучение в измерительном плече интерферометра (при наличии только одного лазерного излучателя) сдвинуть на частоту f ~ 1100 МГц относительно электромагнитной волны в опорном плече, то вследствие интерференции между опорной и измерительной волнами, в регистрируемом квадратичным фотоприемником сигнале возникают биения на разностной частоте f. При прохождении через плазму этот сигнал дополнительно смещается по частоте (модулируется по фазе) на величину d()/dt. После фотоэлектрического преобразования интерференционный сигнал на частоте f + d()/dt подается вместе с опорным сигналом частоты f на аналоговое или цифровое устройство – фазовый компаратор. Одним из вариантов цифрового компаратора, использующегося в интерферометрах, является устройство в состав, которого входят два счетчика. Результаты счета обрабатываются цифровым сумматором, и полученная сумма подается на цифро-аналоговый преобразователь, который вырабатывает сигнал, пропорциональный , а не cos().

Частотный сдвиг f =  2 между интерферирующими лучами может быть создан различными способами: доплеровским сдвигом за счет отражения излучения от движущегося отражателя, вращающейся дифракционной решеткой, смешением излучений двух частотно стабилизированных лазеров, при использовании двухчастотных лазеров, или с помощью акустооптических ячеек. Одна из многочисленных разработок из Лос-Аламоса гетеродинного интерферометра с квадратурной регистрацией сигнала приведена на рис.12.1. Акустооптическая ячейка Брэгга на основе молибдата свинца (PbMoO₃) в этой схеме выполняет две функции: расщепляет лазерный пучок и обеспечивает сдвиг частоты.

Рис.12.1 Квадратурный интерферометр с акустооптической ячейкой в качестве преобразователя частоты: Г-генератор частоты 80 МГц, ДЧ- делитель частоты пополам, Д-фотодетектор, КФК- фазовый компаратор

Перенос интерференционного сигнала на промежуточную частоту f при условии, что ширина спектра сигнала f<<f, позволяет повысить точность измерений фазовых сдвигов и обеспечить помехозащищенность за счет привлечения радиотехнических методов узкополосного выделения информативного сигнала из шумов различной природы. Перенос информативного сигнала на частоту, существенно превышающую полосу фликкер-шума, и последующее узкополосное гетеродинирование на ВЧ-смесителе с опорным сигналом модуляции позволяет на несколько порядков повысить отношение сигнал/шум. По существу гетеродинное преобразование интерференционных сигналов позволяет приблизиться к квантовому пределу чувствительности, задаваемому спонтанным шумом в генерации лазера.

Е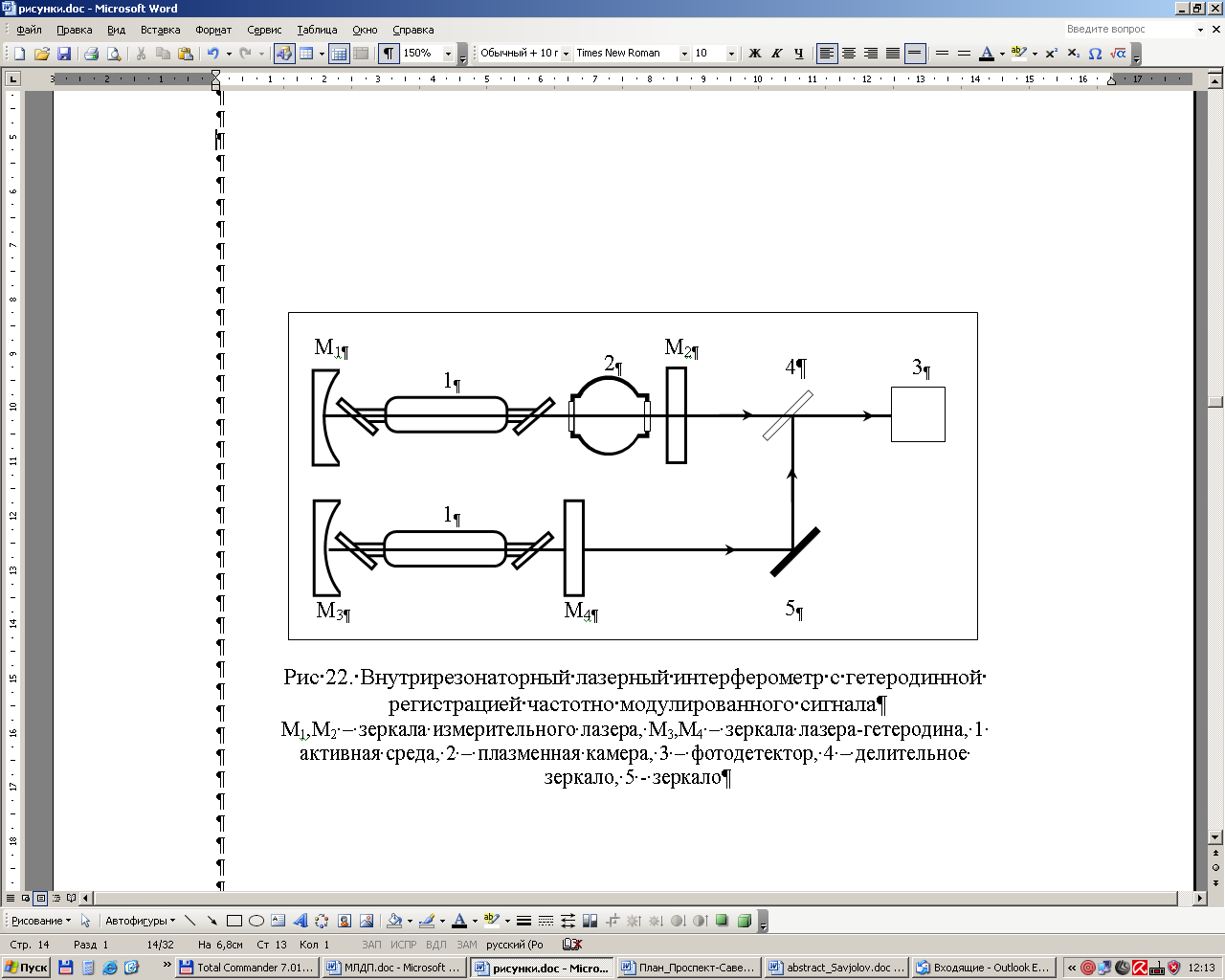 сли в резонатор лазера поместить исследуемый плазменный объект, то изменение показателя преломления n плазмы с линейным размером , будет приводить к изменению оптической длины резонатора L и, соответственно, сдвигу частоты генерации лазера =(n/L). Для измерения величины этого сдвига может быть использована гетеродинная методика с использованием другого однотипного частотно стабилизированного лазера (рис. 12.2). С помощью делительного зеркала 4 амплитуды полей обоих лазеров когерентно смешиваются на квадратичном фотодетекторе 3 на выходе которого выделяется сигнал биений с частотой равной разности частот лазеров. Относительная стабильность разностной частоты двух независимых He-Ne лазеров за временной интервал равный времени существования плазмы была не хуже 10³ Гц, а минимально регистрируемая величина электронной плотности составила =610¹¹см^-2. При использовании He-Ne и СО₂ лазеров чувствительность оценивалась значением 210¹¹ cм^-2.

Максимальная электронная плотность которая может быть измерена таким гетеродинным активным интерферометром определяется разностью частот генерации лазеров. Обычно максимальная величина относительной частотной отстройки генерации непрерывных лазеров ограничивается диапазоном свободной дисперсии их резонаторов. Например, для одномодового He-Ne лазера с длиной резонатора 50 см диапазон свободной дисперсии составляет 300 МГц, соответственно при использовании в качестве гетеродина такого же лазера максимально измеримая электронная плотность составит 210¹⁷ cм^-3.

Использование нелинейного преобразования излучения во вторую гармонику послужило основой схемы двухволнового нелинейного дисперсионного интерферометра предложенного независимо несколькими группами ученых. В этом интерферометре, в отличие от традиционных, отсутствуют зеркала, а используются два нелинейных электрооптических кристалла. Такая оптическая схема обеспечивает высокую виброизоляцию и позволяет размещать оптические элементы интерферометра непосредственно на фланцах диагностических каналов рабочей камеры плазменной установки. Оптическая схема одного из вариантов дисперсионного интерферометра приведена на рис. 12.3. Зондирующее излучение Nd:YAG лазера (₁=1.064 мкм) частично преобразуется в излучение второй гармоники (₂=0.532 мкм) в нелинейном кристалле НК₁, в следствие чего плазменный объем 3 зондируется двумя волнами с частотами  и 2. Для компенсации несоосности зондирующих волн с частотами  и 2 используется перемещаемый в поперечном направлении оптический клин 2. В качестве оптических удвоителей частоты используются кристаллы КТР (KTiOPО₄). За счет синхронизма II-типа оптимальный угол между направлением поляризации излучения основной частоты е_ и направление поляризации быстрой волны P_f⁽¹⁾ в нелинейном кристалле НК₁ составляет 45⁰. Направление поляризации второй гармоники е_2⁽¹⁾, генерируемой НК₁, совпадает с P_f⁽¹⁾. Во втором нелинейном кристалле НК₂ часть излучения на основной частоте снова преобразуется во вторую гармонику е_2⁽²⁾. Вследствие того, что ориентация НК₂ ортогональна НК₁ направление поляризации быстрой волны P_f⁽²⁾ второго нелинейного кристалла ортогональна первому, соответственно, поляризации излучений на удвоенной частоте сформированные до и после прохождения через плазму взаимно ортогональны. Каждая из волн раскладывается поляризационной призмой Глана 5 на две ортогональные компоненты, каждая из которых ориентирована под углом 45⁰ к исходным поляризациям. Таким образом, оба фотоприемника регистрируют сигналы интерференции двух волн е_2⁽¹⁾ и е_2⁽²⁾. За счет скачка фазы на  рад. при отражении от рабочей плоскости поляризационной призмы сигналы с фотоприемников противофазны, что позволяет использовать дифференциальную схему фоторегистрации и существенно снизить уровень флуктуаций из-за нестабильности мощности излучения второй гармоники.

При прохождении через плазму амплитуды полей на основной и удвоенной частоте имеют вид Е₁=cos(t+_p+_v) и Е₂=cos(2t+_p/2+2_v), где _p, _v – фазовые сдвиги, определяемые соответственно плазмой и флуктуациями оптической толщины измерительного отсека, образованного выходной гранью НК₁ и входной гранью НК₂. После повторного удвоения частоты, фильтрации и преобразования поляризаций на квадратичном детекторе выделяется сигнал U~(2_p+2_v)₁-(_p/2+2_v)₂=(3/2)_p пропорциональный только фазовому сдвигу в плазме. Стабилизация мощности до уровня 1.5% и применение дифференциальной схемы фоторегистрации позволили обеспечить чувствительность измерений линейной электронной плотности на уровне 10¹³ см^-2.

Использование в качестве удвоителя частоты кристалла ZnGeP₂ позволяет реализовать аналогичную методику на основе СО₂ лазера.

ЛЕКЦИЯ 13

Если резонатор лазера будет охватывать камеру с исследуемым плазменным объектом, то изменение показателя преломления n плазмы с линейным размером , будет приводить к изменению оптической длины резонатора L.

В 1973 г. для измерения электронной плотности плазмы был предложен интерферометр, в основу которого положено явление двухмодовой конкуренции в He-Ne лазере, работающем на переходе =3.39 мкм с уширением близким к однородному. Двухмодовый режим генерации в таком лазере реализуется за счет введения в резонатор двух фазоанизотропных элементов Ф₁, Ф₂, выполненных из кристаллического кварца обладающего двулучепреломлением, в виде клиньев с одинаковой ориентацией осей анизотропии (рис. 13.1а).

Рис.13.1 Двухмодовый лазерный интерферометр.

Соседние по частоте моды ₁ и ₂ такого резонатора линейно поляризованы вдоль главных осей фазовых элементов и, следовательно, ортогональны друг другу. Перемещение клиньев поперек оптической оси лазера (или вращение четвертьволновых пластинок вокруг оси лазера) дает возможность независимого управления частотой межмодового расщепления ₁-₂ и величиной межмодового взаимодействия.

Рис.13.2 Изменение мощности генерации на выделенной поляризации.

Если две соседние продольные моды резонатора занимают симметричное положение относительно центра линии усиления, то возможна одновременная генерация обеих мод в некотором интервале частот отстроек от симметричного положения. Эта величина зависит от межмодового расстояния и степени межмодовой конкуренции. При смещении мод резонатора в пределах интервала  мощность одной моды падает до нуля по линейному закону, а мощность второй растет, при этом общий уровень генерации не меняется. Спектр фазовоанизотропного резонатора удвоен по сравнению со спектром изотропного (той же длины L) из-за снятия вырождения по поляризациям. Каждая мода оказывается расщепленной на две. Следовательно, соседние по частоте моды ₁ и ₂ такого резонатора линейно поляризованы вдоль главных осей фазовых элементов и ортогональны друг другу. В этом случае фотоприемник 3, перед которым расположен поляризатор 4, при непрерывном изменении L зафиксирует периодически повторяющуюся картину, что иллюстрируется осциллограммой на рис. 13.2, т.е. лазер в таком режиме работает как линейный частотно-амплитудный дискриминатор с регулируемой крутизной.

Таким образом, калибровка прибора сводится к измерению τ , Т и V_max на осциллограмме изменения сигнала с фотоприемника при линейном сканировании длины резонатора (рис.13.2) на величину большую λ/2, например, с помощью пьезокорректора 5 с зеркалом М₁ (рис.13.1). Определение временного поведения (N_el)_t сводится к регистрации ΔV_(t) при работе лазера в режиме конкуренции мод.

Если изменение длины резонатора будет вызвано появлением в нем плазмы с линейной плотностью , то мощность генерации лазера изменится также линейно на любой из выделенных мод и будет пропорциональна изменению . Для определения электронной плотности плазмы можно использовать формулу

. (13.1)

За счет большого усиления (~50 дБ/м) активной среды He-Ne лазера на длине волны 3,39 мкм, он способен работать в условиях высокого уровня потерь, связанных с отражением и поглощением в оптических окнах плазменной камеры и рассеянием излучения в плазме. Так, например, с использованием такого интерферометра были проведены исследования динамики электронной плотности плазмы на крупномасштабных установках с линейными размерами более 1,5 м (токамак Т 12).

Достоинством двухмодового интерферометра, кроме линейности аппаратной функции, является возможность плавно управлять её крутизной (чувствительностью измерений) изменением величины межмодовой связи ( отношения τ/Т ). τ/T можно варьировать, изменяя величину диапазона двухмодовой конкуренции. Большая крутизна аппаратной функции интерферометра обеспечивает высокое превышение величины регистрируемого сигнала над шумами фотоприёмника и, следовательно, высокую чувствительность измерений. Максимальная чувствительность интерферометра составила =510¹² cм^-2 и ограничивается естественными шумами лазера. Максимальное временное разрешение такого интерферометра 10^-7 с ограничивается временем установления режима двухмодовой генерации.

Практически одновременно с появлением лазеров было отмечено, что попавшее в лазер внешнее излучение влияет на режим его генерации. Так уже в 1963 году в было впервые показано, что изменение расстояния между лазером и зеркалом, отражающим излучение назад в лазер, приводит к модуляции мощности генерации лазера на доплеровской частоте, соответствующей скорости перемещения зеркала. При этом минимумы интенсивности излучения совпадают с прохождением зеркалом точек, которые соответствуют нечетному числу полуволн. Даже при удалении зеркала на расстояние более 5 м (в лазер возвращалось менее 1% выходной мощности) величина модуляции составляла около 50% от общей мощности генерации лазера.

Принцип работы таких лазерных систем основан на хорошо известном в радиоволновом и СВЧ- диапазонах автодинном эффекте, присущим всем автоколебательным системам. По существу, лазер выполняет функции когерентного гетеродинного приемника и усилителя сигнала, при этом квадратичное детектирование регистрируемого излучения происходит непосредственно в активной среде лазера еще до фотоприемника. Такой режим работы лазера будем называть “внутрилазерным приемом”. По существу для любых отражателей, в том числе и с диффузным характером отражения, справедлива модель лазера с внешним зеркалом. При возвращении в лазер отраженной волны происходит ее интерферометрическое сложение с внутренней волной лазера. Это эквивалентно изменению потерь лазерного резонатора и его длины. Если усиление активного элемента и потери резонатора близки друг к другу, то при слабой отраженной волне происходит существенное изменение мощности генерации лазера, обеспечивая высокую крутизну соответствующей аппаратной функции. Одновременно изменяется частота генерации в такой же гармонической зависимости от оптической длины пути до отражателя, как и для мощности генерации, но квадратурно ей.

На рис.13.3 представлена оптическая схема, в которой возвращенное излучение от каждой моды взаимодействует с внутренней волной другой моды, соответственно со сдвигом частоты, равным заданному в лазере межмодовому частотному расщеплению. Для этого генерируемые моды должны быть поляризованы взаимно ортогонально. На пути излучения к внешнему отражателю установлена четвертьволновая фазовая пластинка (/4). При двукратном прохождении через нее, до отражателя и обратно, излучения мод “обмениваются” своими поляризациями. На рисунке показан поляризатор, выделяющий одну из мод, для регистрации фотоприемником модуляции ее мощности.

Таким образом, возвращенное излучение от каждой моды взаимодействует с внутренней волной другой моды, соответственно со сдвигом частоты, равному заданному в лазере межмодовому частотному расщеплению f=₂ -₁. При таком перекрестном воздействии мод друг на друга через внешний отражатель в лазере возникает модуляция частоты межмодовых биений и интенсивностей обеих мод р_1,2 на частотах f с амплитудами гармонически и квадратурно друг другу зависящими от оптической длины пути nL до отражателя и линейно от его амплитудного коэффициента отражения .

Рис.13.3 Оптическая схема интерферометра с внутрилазерным приемом.

В выражениях и для модуляции мощности мод, и для модуляции их разностной частоты, содержится информация, как об эффективном коэффициенте отражения , так и об оптической длине пути nL до отражателя. Для разделения этой информации, наряду с сигналом модуляции мощности в одной из мод, может быть использован сигнал межмодовых биений.

На рис. 13.4 приведена оптическая схема интерферометра, основой которого служит зеемановский двухчастотный He-Ne лазер на длине волны =3,39 мкм. Продольное магнитное поле в активной среде создается однослойной обмоткой навитой непосредственно на газоразрядной трубке. Излучение одной из частот (мод) выделяется четвертьволновой пластинкой и поляризатором П₁. Сигнал модуляции мощности регистрируется фотоприемником D₁ и поступает через предварительный усилитель на смеситель 3 (рис. 3.31в). Второй фотоприемник D₂ с помощью поляризатора П₂ регистрирует сигнал биений, который после предварительного усилителя делится узкополосными фильтрами 1 и 2 по гармоникам. Часть сигнала первой гармоники используется в качестве опорного сигнала в смесителе 3. На его выходе после устранения несущей частоты f формируется первый информативный сигнал

(13.2)

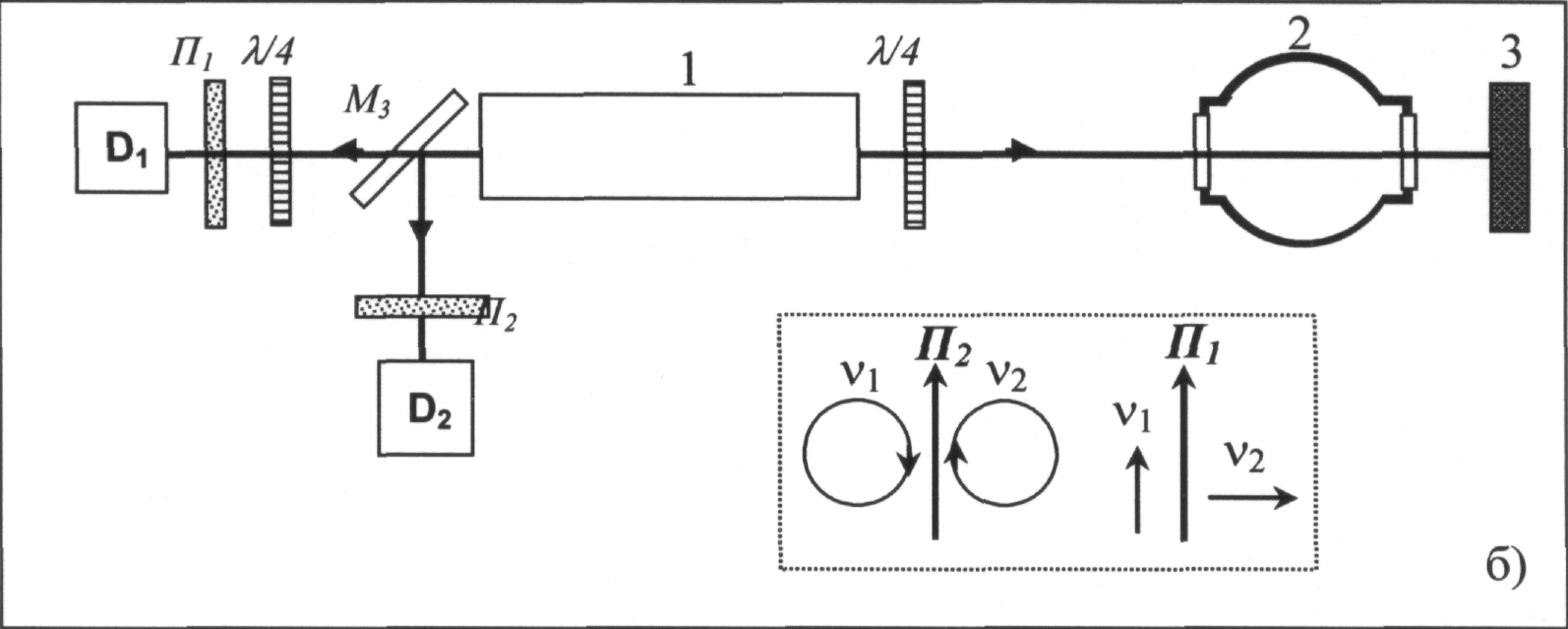
Рис.13.4 Схема измерений

Другая часть сигнала первой гармоники после удвоителя частоты 4 используется как опорный сигнал в смесителе 5, куда поступает сигнал второй гармоники. На выходе формируется второй информативный сигнал

(13.3)

Можно сформулировать основные требования, которым должен удовлетворять интерферометр на основе внутрилазерного приема для решения широкого круга измерительных и диагностических задач:

• Интерферометр должен сохранять работоспособность при использовании удаленных отражателей с низким эффективным коэффициентом отражения и, соответственно, сочетать двухлучевую оптическую схему с высокой крутизной аппаратных функций;

• Для повышения чувствительности измерений регистрация интерференционного сигнала должна проходить на высокой несущей частоте;

• При проведении измерений в диапазоне много больше длины волны интерферометр должен обладать такой же высокой чувствительностью, как и при измерениях в одной полосе интерференции и, соответственно, иметь два квадратурных измерительных канала;

• Интерферометр должен иметь простую и надежную конструкцию, предоставляющую возможность универсального использования прибора.

ЛЕКЦИЯ 14

В случае, когда плазма вносит в электромагнитную волну фазовый сдвиг, существенно превосходящий длину волны, для восстановления динамики электронной плотности во времени обычно достаточно проводить измерения в режиме счета минимумов и максимумов интерференционных полос. При этом, как было показано выше, неоднозначность определения знака изменения фазы может быть устранена введением дополнительной фазовой модуляции с частотой превосходящей максимальную частоту изменения интенсивности при перемещении интерференционных полос через диафрагму детектора. При малых фазовых сдвигах и проведении измерений в окрестности начальной фазы ₀=/2 изменение фототока детектора однозначно воспроизводит изменение показателя преломления плазмы. Однако часто в плазменном эксперименте приходится сталкиваться с ситуацией, когда фаза электромагнитной волны при распространении в плазме изменяется в широком диапазоне от долей периода до единиц или более интерференционных полос (1<</2>>1). В этих условиях из-за нелинейной дифференциальной чувствительности интерференционных измерений, особенно при немонотонном изменении плотности плазмы во времени и при условии, что значительная доля фазовых сдвигов приходится на область с близкой к нулю дифференциальной чувствительностью, восстановление действительного закона изменения фазы представляет серьезную проблему. Кроме того, регистрируемый интерференционный сигнал линейно зависит от произведения амплитуд зондирующего и опорного пучков, поэтому вариации этого произведения во времени могут быть ошибочно приняты за изменения фазового сдвига.

Устранить существующие трудности позволяет квадратурная методика фотоэлектрической регистрации, имеющая однородную дифференциальную чувствительность во всем диапазоне изменений. Впервые в оптической диагностике плазмы квадратурная схема была применена в середине 70-х годов ХХ столетия Бухенауэром и Джекобсоном. Вместе с тем в СВЧ диагностике эта методика стала применяться значительно раньше, и известна под названием «интерферометр с полярной индикацией». В практике прецизионных измерений перемещений приборы на основе квадратурной методики получили название «интерферометры с реверсивным счетом полос».

Основная идея квадратурных интерферометров сводится к использованию двух интерференционных сигналов, сдвинутых друг относительно друга на четверть периода. На выходе такого интерферометра формируются два сигнала вида:

(14.1)

, (14.2)

где U₀(t) – содержит мультипликативную помеху, связанную с флуктуациями интерферирующих полей. Преобразование этих сигналов, подобное преобразованию декартовой системы координат в полярную, позволяет восстановить закон изменения оптической длины

(t)=arctg(U₁(t)/U₂(t)). (14.3)

Заметим, что операция деления сигналов друг на друга позволяет устранить влияние медленно меняющейся по сравнению с функциями sin((t)) и cos((t)) мультипликативной помехи U₀(t) в интерференционном сигнале.

Квадратурный интерферометр позволяет однозначно регистрировать практически любые набеги фазы с высокой однородной дифференциальной чувствительностью. Кроме того, он не только устраняет ошибки, связанные с изменением интенсивности зондирующего излучения I₀ вследствие поглощения в плазме или изменения эффективного коэффициента отражения зеркал в процессе проведения измерений, например, из-за модификации отражающей поверхности, но и дает возможность контроля этих процессов

. (14.4)

На сегодняшний день наиболее эффективная реализация алгоритма обработки квадратурных сигналов возможна с использованием цифровых систем сбора данных с их последующей компьютерной обработкой. Отметим, что преобразование (14.3) позволяет однозначно измерить сдвиг фаз только в области главных значений функции arctg, в пределах одного фазового цикла -< рад., поэтому, если в процессе измерений изменение происходит на величину превышающую /2, то происходит скачок текущего значения аrctg(U₁/U₂) на 2 рад с потерей предыдущей информации о фазе. Обычный алгоритм «развертывания фазы» т.е. преобразование значений приведенной фазы на интервалах [-,] в непрерывно изменяющиеся значения фазы заключается в обнаружении скачков значений фазы между двумя соседними точками, превышающих величину  рад. Добавлением или вычитанием скачков фазы 2 рад можно восстановить непрерывность фазовой функции.

Квадратурные сигналы могут быть сформированы различными способами, например, с использованием двух фотоприемников, размещенных в различных участках интерференционной полосы, расстояние между которыми равно четверти ее ширины. Это достигается перемещением диафрагмированных детекторов поперек направления интерференционной полосы. Текущее значение разности фаз сигналов с фотодетекторов при юстировке можно контролировать на двухкоординатном осциллографе, в режиме развертки у(х) (рис.14.1). Если при предварительной настройке обеспечить модуляцию длины одного из плеч интерферометра порядка длины волны, то на экране осциллографа в общем случае будет наблюдаться эллипс. При равенстве амплитуд сигналов с детекторов квадратурному режиму соответствует окружность.

Однако этот способ формирования квадратурных каналов имеет ряд недостатков. Во первых, используется только малая часть интенсивности, вырезанной диафрагмами из суммарного светового потока, в результате чего снижается отношение сигнал/шум фотоэлектрической регистрации, во вторых – возможное изменение ориентации полос и их ширины в процессе проведения измерений приводит к нарушению взаимной юстировки детекторов.

В интерферометре настроенном в режим бесконечно широкой полосы квадратурные сигналы можно сформировать с помощью четвертьволновой пластинки, установленной под 45⁰ к плоскости поляризации зондирующего излучения и взаимно ортогональных поляризаторов. Четвертьволновая пластинка в этом случае трансформирует поляризацию излучения на выходе из интерферометра из линейной в круговую, которая может быть представлена как суперпозиция двух линейно и ортогонально поляризованных компонент сдвинутых по фазе на /2. Пространственное разделение квадратурных компонент проводится с помощью поляризационной призмы или взаимно ортогональных поляризаторов.

Оптические методы формирования квадратурных измерительных каналов в интерферометрии являются наиболее универсальными и могут быть использованы при измерениях без ограничения на величину фазового сдвига. При этом квадратурные сигналы формируются в пространственно разделенном по каналам излучении и детектируются несколькими детекторами. В случае, когда интерференционный сигнал с шириной спектра f перенесен на промежуточную частоту f (f<<f), то квадратурные каналы могут быть сформированы в схеме с одним детектором на стадии электронного преобразования электрического сигнала в схеме квадратурного фазового компаратора. Фототок с детектора усиливается и делится по двум каналам. Для того чтобы исключить возможную амплитудную модуляцию в сигнале усилитель должен работать в насыщении. Один сигнал поступает непосредственно на ВЧ-смеситель, второй - задерживается на 90⁰ и попадает на другой смеситель. На опорный вход каждого смесителя подается сигнал на частоте модуляции когерентный с сигналом акустооптического модулятора.

Для интерферометра, принцип действия которого был изложен выше, размер внешнего резонатора может достигать десяти и более метров. Поскольку размеры проектируемого Т-15М не превосходят эти значения, как в вертикальном, так и в горизонтальном направлении можно рассматривать возможность использования «Лиры» для диагностики на Т-15М.

Рис.14.2. Распределение электронной плотности вблизи сепаратриссы.

Диагностика центральной области плазмы трудностей принципиального характера не представляет, т.к. значение N_e l при сквозном вертикальном зондировании будет существенно превышать вклад от нейтральной компоненты N_a l и основная трудность в применении интерферометра будет связано с защитой (или учетом вклада в набег фазы интерференционного сигнала) от вибраций. Более трудную задачу представляет исследование плазмы в области диверторных пластин (рис.14.2).

Очевидно, что исследовать плазму вблизи Х-точки и в той области, где плазма активно взаимодействует с диверторными пластинами, возможно только в направлении близком к горизонтальному. В этом случае возникает проблема деградации поверхности зеркала, которое должно быть размещено на внутренней стенке вакуумной камеры. По-сути, предлагаемому в настоящей работе интерферометру альтернативы на сегодняшний день не имеется, поскольку появляется обоснованная надежда использовать в качестве третьего «зеркала» интерферометра-рефлектометра либо непосредственно поверхность диверторных пластин, когда падение луча зондирующего излучения близко к нормальному, либо располагаемой за ними пластины при косом падении. При этом в последнем случае отражающую пластину необходимо соответствующим образом соориентировать и выполнить из материала наиболее стойкого к потоку корпускулярного излучения. Как следует из всего вышесказанного требования к коэффициенту отражения не являются определяющими, более того отражающие свойства поверхности будут контролироваться при проведении измерений на двух длинах волн, что может предоставить в руки экспериментаторов информацию о характере модификации поверхности в динамике.

Исходя из предоставленной авторам «ЛИРЫ» разработчиками Т-15М графической информации о распределении электронной и нейтральной компоненты в области сепаратриссы, были сделаны оценки величин линейных концентраций для трех выделенных направлений вблизи Х-точки, когда падение зондирующего излучения на поверхность дивертора близко к нормальному. Результаты для линейной электронной концентрации представлены на рис.14.2. Значения для нейтральной компоненты по отношению к электронной составляют (от верхней к нижней прямой ), соответственно, 4%, 7% и 60%. Как известно, для водорода вклады в набег фазы интерференционного сигнала для =0,63 мкм от названных компонент сравниваются при степени ионизации плазмы 3%, т.е. когда значение концентрации нейтралов превышает электронную примерно в тридцать раз, что существенно выше полученных величин. Таким образом две длины волны зондирующего излучения могут быть с полным основанием использованы для разделения вкладов в сигнал от электронной концентрации и механических перемещений элементов конструкции установки. Очевидно, что механические вибрации будут существенно превышать вклад от электронов плазмы и значительные усилия разработчиков диагностического прибора будут сосредоточены не только на решении физических проблем по созданию интерферометра на =0,63 мкм, но и на разработке соответствующей электронной аппаратуры для обработки сигнала.

На рис.14.3 приведено предполагаемое расположение элементов диагностической аппаратуры для исследования диверторной плазмы на пректируемой установке Т-15М. Оптический блок расположен в стойке вместе с блоком электроники ( на рис. выделен зеленым цветом). Расстояние от камеры Т-15М и место расположения необходимо необходимо дополнительно согласовывать. Для ввода излучения (красный цвет на рис.) в камеру через нижний диагностический патрубок и изменения направления зондирования создается конструкция из двух 100% зеркал размещаемых в трубе прямоугольного сечения, изображенной синим цветом на рисунке, которая располагается вертикально между двумя катушками. Оба зеркала закрепляются на двух юстировочных головках, которые позволят производить как вертикальное их перемещение, так и вращение вокруг горизонтальных осей. Это позволит произвести зондирование практически во всем обьеме занимаемом плазмой в области вокруг Х-точки. С точки зрения экспериментаторов пути зондирования, а значит и местоположения отверстий на диверторных пластинах для ввода излучения оптимальны.

Рис.14.3 Расположение диагностической аппаратуры

ЛЕКЦИЯ 15

В результате проведения «хордовых» измерений были получены интегральные распределения линейной электронной плотности , где , тогда как наибольший интерес представляют локальные значения параметров, характеризующих состояние плазмы.

В общем виде эта задача не имеет однозначного решения, однако, если мы допустим упрощающее предположение об аксиальной симметрии плотности n(r), то решение возможно. В этом случае это выражение можно переписать в виде

(15.1)

Выражение (15.1) представляет собой интегральное уравнение Абеля. Его общий вид

(15.2)

Таким образом, наша задача фактически сводиться к отысканию функции f(r) по измеренным значениям g(y). Решение уравнения (15.2) хорошо известно:

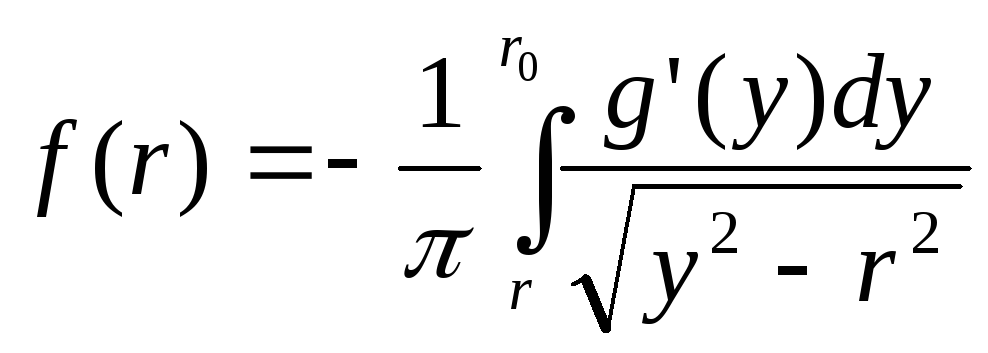(15.3)

Оно является точным, однако применить его непосредственно на практике обычно не удается. Выражениям вида (15.3) чувствительны к погрешностям, содержащимся в экспериментальной кривой g(y), что прямо связано с наличием производной g’(y) в этой формуле. Поэтому для нахождения функции f(r) применяют различные математические приемы.

В МИФИ в среде программирования LabView написана программа абелизации по методу Пирса. Для демонстрации ее работы выбрана функция , по этой функции аналитически найдена функция g(y). Интервал значений у от 0 до 1 разбивался на 10 точек. В каждой точке бралось значение g(y), к нему прибавлялась случайная погрешность с равномерным законом распределения и амплитудой 10% от величины g(y). Далее по этим десяти значениям программа восстанавливает значения f(r). Из рисунка 15.1 видно, то метод Пирса действительно позволяет получать устойчивые значения локальных величин при небольшом числе хорд зондирования.

Рис. 15.1 Проверка метода Пирса. Синяя кривая соответствует точной аналитической зависимости, черные точки соответствуют восстановленным по методом Пирса значениям f(r).

Использование этого алгоритма позволяет проводить восстановление локальных значений линейной электронной плотности из экспериментально измеренных интегральных значений вдоль оси зондирования.

Кратко о сути метода диагностики интерференционной картины. Если предположить применимость геометрической оптики, то для осесимметричных объектов при переходе в цилиндрическую систему координат получим заменой

, (15.4)

где δ(y) – сдвиг интерференционных полос, n(r) – оптическая плотность среды. Соотношение (15.4) представляет собой интегральное уравнение Абеля. Формальное обращение уравнения (15.4) приводит к уравнению

, (15.5)

Уравнение и используется для вычисления оптической плотности среды по известной зависимости смещения от радиальной координаты.

Стандартный ("ручной") метод обработки представляет собой последовательность достаточно трудоемких шагов:

1. Фотографирование изображения интерференционных полос.

2. Вычисление по изображению смещения интерференционных полос от невозмущенного состояния.

3. Вычисление интеграла Абеля по численной зависимости смещения от радиуса.

Уже на первом шаге возникает проблема: при фотографировании из-за постороннего шума, "паразитных" дифракции и интерференции на элементах установки и фотосистемы качество получаемого изображения обычно весьма невысокое. Соответственно с достаточной точностью вычислить смещение интерференционных полос очень сложно. А, как известно, обратная задача Абеля, решение которой дает значение оптической плотности, неустойчива к малым изменениям краевых условий. Соответственно, чаще всего получаются результаты с крайне низкой точностью.

Автоматизация процесса обработки позволяет значительно сократить время анализа экспериментальных данных и увеличить точность получаемых результатов.

Для получения численной зависимости смещения интерференционных полос от радиуса изображение разбивается на области одинаковой ширины (вдоль радиальной координаты). На границе каждой области определяется сдвиг в экранных точках конкретной полосы от невозмущенного положения на краю изображения. Затем данные пересчитываются в единицы длины волны.

Для аппроксимации функции смещения полос кусочно-параболической функцией используется интерполяционный полином Лагранжа степени 2 – выражение для параболы, проходящей через три заданные точки.

Получить трехмерное изображение предмета можно с помощью голографии. При исследовании плазмы применение нашла голографическая интерферометрия методом двух экспозиций.

На одной и той же фотопластинке регистрируют две голограммы одного объекта в разные моменты времени t₁ и t₂. Напомним выражения для освещенностей Е₁ и Е₂ для каждой экспозиции:

Для простоты примем, что прозрачность полученного негатива по амплитуде изменяется пропорционально падающей на него энергии Е, т. е. сумме освещенностей (при этом предполагается, что времена экспонирования равны):

Если объект не перемещается и не деформируется между двумя экспозициями, то освещенности Е₁ и Е₂ совершенно идентичны, а все происходит так, как при регистрации одной голограммы с двойной выдержкой, т. е. получаем «сумму» двух голограмм.

Малейшее изменение положения или формы объекта в промежутке между двумя регистрациями изменяет фазу волны, испускаемой объектом (φ₁ ≠ φ₂). Второй член выражения для полной энергии Е, соответствующий изображению, как раз содержит информацию об амплитуде а и фазах φ₁ и φ₂. Амплитуды волн, испускаемых в направлении изображения, пропорциональны вариациям прозрачности голограммы. Теперь все происходит как при восстановлении суперпозиции двух изображений, когерентных между собой и очень мало отличающихся друг от друга.

Эти изображения интерферируют и наблюдаемые полосы, как и в классическом интерферометре, соответствуют вариациям фазы φ₁ - φ₂, которые возникают в промежуток времени между двумя экспозициями.

Таким образом, практическое применение интерферометрии с двойной экспозицией отличается замечательной простотой. Составные элементы классического интерферометра (зеркала, полупрозрачные пластинки) здесь совершенно бесполезны. Регулировка очень проста и состоит в небольшом смещении источника между двумя экспозициями, что позволяет создать систему интерференционных полос в поле изображения. Наблюдение в полосах бесконечной ширины осуществляется автоматически, если источник и другие элементы установки не претерпевают никаких изменений.

В обычной интерферометрии обе сравниваемые волны формируются одновременно или с очень небольшой временной задержкой, максимальная величина которой определяется временем когерентности используемого источника света и составляет обычно 10^-11—10^-9 сек и никогда не превышает 10^-6-10^-5 сек.

Голография позволяет зафиксировать световую волну и восстановить её в любой нужный момент времени. Поэтому голографическая интерферометрия не связана требованием одновременности формирования волн, и это обстоятельство открывает перед нею ряд интересных возможностей, которые в обычной интерферометрии реализованы быть не могут.

В голографической интерферометрии могут сравниваться последовательные состояния одного и того же объекта. Это автоматически обеспечивает волну сравнения, повторяющую во всех мельчайших подробностях волну, рассеянную объектом в исходном состоянии. Благодаря этому, голографическим интерференционным методом можно исследовать объекты неправильной формы и даже шероховатые, диффузно отражающие свет.

В обычной интерферометрии это невозможно, так как волна сравнения может воспроизвести все детали волны от объекта лишь в том случае, если он имеет достаточно простую форму. Поэтому в обычной интерферометрии обычно исследуются объекты простой формы и совершенной оптической поверхности.

Особенность голографической интерферометрии существенно снизила требования к качеству интерферометрической оптики, поскольку сравниваются волновые фронты, прошедшие по одному и тому же каналу, а не по двум различным каналам, как в обычной интерферометрии. Поэтому обе интерферирующие волны в одинаковой степени искажаются погрешностями оптических деталей, и в силу дифференциальности метода это не сказывается на виде интерференционной картины.

ЛЕКЦИЯ 16

Рассмотренные нами лазерные методы диагностики, несмотря на их разнообразие, объединяет то, что информация, получаемая в ходе измерений, носит интегральный характер. Для получения информации о локальных параметрах плазмы необходимо, используя a priori предположения о характере распределения исследуемого параметра плазмы, воспользоваться той или иной моделью для решения некорректной задачи.

Использование рассеяния лазерного излучения в плазме обладает несколькими несомненными преимуществами:

- локальность измерений в сочетании с их бесконтактностью;

- непосредственная интерпретация полученных сигналов в терминах измеряемых параметров плазмы, что обусловлено проработанностью лежащих в основе методики физических принципов;

- возможность определения таких важных параметров, как n_е и Т_е в широком диапазоне их значений без существенной модификации диагностической аппаратуры;

- принципиальная возможность наряду с n_е и Т_е измерять такие параметры, как напряженность магнитных полей в плазме, уровень и спектр турбулентности, ионная температура Т_i, эффективный заряд плазмы Z_эф.

Рассеяние лазерного излучения может происходить как на свободных электронах, так и на флуктуациях плотности плазмы.

Вопрос о том, происходит ли рассеяние на флуктуациях плотности независимо движущихся электронов или же спектр рассеяния отражает коллективные движения плазмы, решается сравнением двух величин: дебаевской длины λ_D и модуля волнового вектора k. С этой целью Солпитер ввел параметр α, определяющий характер рассеяния:

На практике для его вычисления удобно использовать формулу

где λ_i — длина волны, нм; n_е — электронная плотность, см^-3; Т_е — электронная температура, эВ. Рассмотрим частные случаи:

1. α << 1 — рассеяние происходит на индивидуальных, независимо движущихся электронах. Для максвелловcкой плазмы спектр рассеяния — гауссова кривая;

2. α ≥ 1 — случай рассеяния на крупномасштабных колебаниях плотности, которые могут носить либо турбулентный, либо тепловой характер, так как и в спокойной плазме существует ненулевой ("тепловой") уровень характерных для плазмы типов колебаний (ленгмюровские, ионно-звуковые и т.д.).

Процесс рассеяния проще всего пояснить, рассматривая рассеяние плоскополяризованной электромагнитной волны на первоначально покоящемся свободном электроне (рис. 15.1). Переменное электрическое поле падающей волны Е_i вызывает колебания электрона с частотой этой волны ω_i. Излучение носит дипольный характер, дифференциальное эффективное сечение рассеяния определяется выражением.

(15.1)

здесь r₀— классический радиус электрона, равный 2,8 ٠ 10^-13 см; φ₀ — угол между направлением Е_i и волновым вектором рассеянного излучения k_s.

Интегрирование формулы (15.1) по телесным углам дает полное эффективное (так называемое томсоновское) сечение

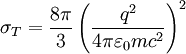
Или для электрона

Рис. 15.1. Излучение электрона под действием падающей электро-магнитной волны	Рис. 15.2. Спектры рассеянного излучения с учетом релятивистских поправок для рубинового лазера при различных Те

Малое значение этого сечения приводит к необходимости применять в качестве источника излучения мощные импульсные лазеры. Введем вектор рассеяния, равный разности волновых векторов падающей и рассеянной волн:

где θ — угол рассеяния (см. рис. 15.1). Если электрон движется со скоростью v_e, то частота рассеянного излучения ω_s сдвинута относительно ω_i:

(15.2)

Таким образом, сдвиг частоты ω определяется проекцией скорости электрона v_e именно на введенный выше вектор k.

Из формулы (15.2) ясно, что лазерное рассеяние можно использовать для определения макроскопических скоростей электронов (скорость пучка, скорость вращения плазменного шнура, токовая скорость электронов).

Если корреляция между рассеивающими электронами отсутствует, а распределение электронов по скоростям описывается максвелловским распределением с электронной температурой Т_е, то спектр рассеянного излучения P_s (ω) при θ = π/2 представляется формулой

(15.3)

где а и b — постоянные коэффициенты.

Спектр излучения описывается в этом нерелятивистском случае гауссовой кривой с шириной на полувысоте Δλ_1/2 ~ T_е^1/2. Для лазера на рубине (λ_i = 694,3 нм)

где Δλ_1/2 - полуширина спектра, нм; Т_е — электронная температура, эВ. В более общем случае, т.е. при θ ≠ π/2, Δλ ~ λ_i٠(Т_е)^1/2٠sin(θ/2).

Практически обработка спектра сводится к построению его в координатах lnP_s(Δλ) ~ (Δλ)², проведению по экспериментальным точкам прямой линии методом наименьших квадратов и нахождению ее наклона, т.е. значения T_e^-1.

Увеличение скорости электронов, а соответственно и температуры Т_е, требует релятивистского рассмотрения проблемы рассеяния волны электронами, начиная примерно с Т_е = 1 ÷ 1,5 кэВ. Основное отличие релятивистских спектров рассеяния P_s(λ_s) от гауссовой кривой (15.3) заключается в сдвиге с ростом Т_е максимума P_s в коротковолновую область спектра. Этот факт проиллюстрирован на рис. 15.2, на котором воспроизведены некоторые из кривых для лазера на рубине и случая θ = π /2. Спектр рассеянного излучения обычно аппроксимируют функциями вида:

здесь х = (λ_s - λ_i) / λ_i; Т_е — электронная температура, кэВ; θ — угол рассеяния, равный π /2.

На процесс рассеяния оказывает влияние наличие магнитного поля В. Теоретический анализ показывает, что такое влияние может проявиться лишь при малом угле ψ между вектором рассеяния k и нормалью к направлению поля В. В предельном случае (ψ → 0 при фиксированных значениях |В| и Т_е) спектр стремится к виду, показанному на рис. 15.3. Спектр состоит в этом случае из пиков, частотный интервал между которыми равен электронной циклотронной частоте ω_се. При конечном угле ψ полуширина отдельных пиков пропорциональна величине kv_esin ψ, где v_e — тепловая скорость электронов.

Рис. 15.3. Спектр рассеяния на электронах в магнитном поле для случая ψ → 0

Глубина модуляции спектра рассеяния определяется отношением полуширины отдельных пиков к циклотронной частоте ω_се. В качестве параметра используют величину α_се = ω_ce/(kv_e sin ψ). Различить отдельные пики в спектре можно, начиная со значения α_се ≈ 2. Таким образом, величину |В| можно найти по расстоянию между отдельными циклотронными пиками, а направление поля В, — по направлению наблюдения k_s, при котором имеет место max модуляция спектра.

Более строгий и общий подход к описанию рассеяния электромагнитной волны плазмой заключается в разбиении объема плазмы на ряд элементарных ячеек и в изучении корреляции между флуктуациями плотности электронов в этих ячейках при различных процессах, происходящих в плазме. Возникающие при этом ситуации иллюстрируются схемами типа приведенной на рис. 15.4. Пусть в плазме распространяется волна (в направлении вектора рассеяния), встречая периодическую структуру возмущений плотности n_е с шагом λ. Если дополнительный набег фазы для излучения, рассеянного объемом 2 (по отношению к точке 1) составляет 2π, то эти объемы дают синфазное излучение в направлении рассеяния k_s. Условием выполнения этого требования является соотношение λ_i = 2λ sin (θ/2), эквивалентное условию k_λ = (4 π / λ_i ) sin (θ/2) = k.

Таким образом, будем получать информацию о периодических флуктуациях величины n_е в направлении, параллельном k, с периодом λ = 2π /|k|. Иными словами, выбор схемы измерений и длины волны зондирующего излучения λ,- дает возможность изучать ориентацию в пространстве, частоту и пространственный масштаб флуктуации плотности. Это положение составляет физическую основу для развития, например, методов изучения турбулентности по спектрам рассеянного излучения.

Рис. 15.4. Рассеяние на простран-ственно-периодических флуктуациях плотности плазмы	Рис. 15.5. Вид спектра рассеянного излучения при рассеянии на крупномасштабных (по сравнению с дебаевским радиусом) флуктуациях

Для случая Т_е ≈ T_i спектр изображен на рис. 15.5. В спектре присутcтвуют так называемые электронные пики как результат рассеяния на обусловленных плазменными колебаниями флуктуациях плотности. Приближенно положение этих пиков в спектре соответствует частотам ω_i ± ω_pe , где ω_ре - электронная плазменная частота.

Помимо электронных пиков в спектре рассеянного излучения присутствует при α >> 1 ионный пик. Форма его зависит от отношения Т_e/Т_i и эффективного заряда Z. При T_i >> Т_е центральная ионная линия описывается гауссовым профилем с полушириной, пропорциональной Т_i^1/2 . Промежуточный случай спектр с Т_е/Ti ≈ 1 (см. на рис. 15.5.) Форму ионного пика удобно характеризовать с помощью параметра β, вводимого соотношением

Кроме этого существует так называемое рэлеевское рассеяние, названное в честь британского физика Джона Рэлея, который исследовал его в 1871 г. Основные черты рэлеевского рассеяния — это рассеяние света без изменения длины волны (называемое также упругим рассеянием) на частицах, неоднородностях или других объектах, когда частота рассеиваемого света существенно меньше собственной частоты рассеивающего объекта или системы. Эквивалентная формулировка — рассеяние света на объектах, размеры которых меньше его длины волны.

Для рассеивания на осцилляторе массы m, с зарядом q и собственной частотой ν₀ сечение рассеяния σ_R пропорционально четвёртой степени частоты рассеиваемого света ν:

Это выражение и вывел Джон Рэлей.

Сечение σ_R зависит от угла рассеяния θ между направлениями падающей и рассеянной волн:

Рассеянная волна линейно поляризована вдоль направления, перпендикулярного плоскости, проходящей через направления распространения падающей и рассеянной волн.

При приближении частоты падающего света к собственной частоте рассеивающей частицы рэлеевское рассеяние переходит в томсоновское.

Рассеяние света связано с вынужденными колебаниями атомных электронов в поле падающей световой волны. Если частота падающего на атом света совпадает с одной из собственных частот атома, то возникает резонанс и атомные электроны раскачиваются падающим светом гораздо сильнее, чем «вдали» от резонанса. Соответственно интенсивность рассеянного света резко увеличивается. Это явление было обнаружено Робертом Вудом в 1905 году и стало называться резонансной флуоресценцией. Большая величина эффективного сечения резонансной флуоресценции при лазерном возбуждении позволяет регистрировать с ее помощью одиночные атомы.

Молекулярное рассеяние света еще разнообразнее атомного. Тепловые колебания молекул приводят к сравнительно медленным изменениям – модуляции амплитуды рассеиваемого света, и при его спектральном анализе это проявляется в виде двух боковых линий – «сателлитов», расположенных симметрично по обе стороны от основной рэлеевской спектральной линии. Между структурой молекулы и частотой спектральных компонентов, появляющихся при рассеянии, имеется жесткая связь, поэтому число таких компонентов и их положение в спектре позволяют определить состав и структуру молекул. Изменение частоты света при рассеянии на молекулах было обнаружено в 1928 г. двумя советскими физиками – Г.С. Ландсбергом и Л.И. Мандельштамом и независимо от них, хотя и несколько позже, индийскими физиками Ч. Раманом и К. Кришнаном. Это явление часто (и не совсем справедливо) называют рамановским рассеянием, в отечественной же литературе принят термин «комбинационное

88