
2.11. Сверхтекучесть изотопа 4He
Экспериментальные данные. Теория Ландау сверхтекучей бозе- жидкости. Возбуждения. Гидродинимика

Квантовые. кристаллы
Квантовый кристалл – кристалл, в котором амплитуда нулевых колебаний частиц, образующих пространственную решетку, сравнима с межатомным расстоянием. Это может привести к заметной вероятности квантового туннелирования частиц и требует учета квантовой статистики
Степень “квантовости” кристалла оценивают через
параметр де Бура, который характеризует отношение
средней кинетической энергии частицы к энергии их |
|
( / a) /(mE)1/ 2 |
~(a / a)2 |
взаимодействия E: |
0 |
Наибольших значений этот параметр достигает у изотопов гелия 3He (L~3.1), 4He (L ~ 2.7). Для сравнения у инертных газов: Ne (0.6), Ar (0.18), Kr (0.10), Xe (0.06)
Единственными в природе реальными квантовыми
2кристаллами являются твердый 3He и 4He
Квантовые. кристаллы
Квантовость проявляется в том, что соседние атомы нельзя рассматривать как частицы, независимо
колеблющиеся около своих положений равновесия
(узлов решетки)
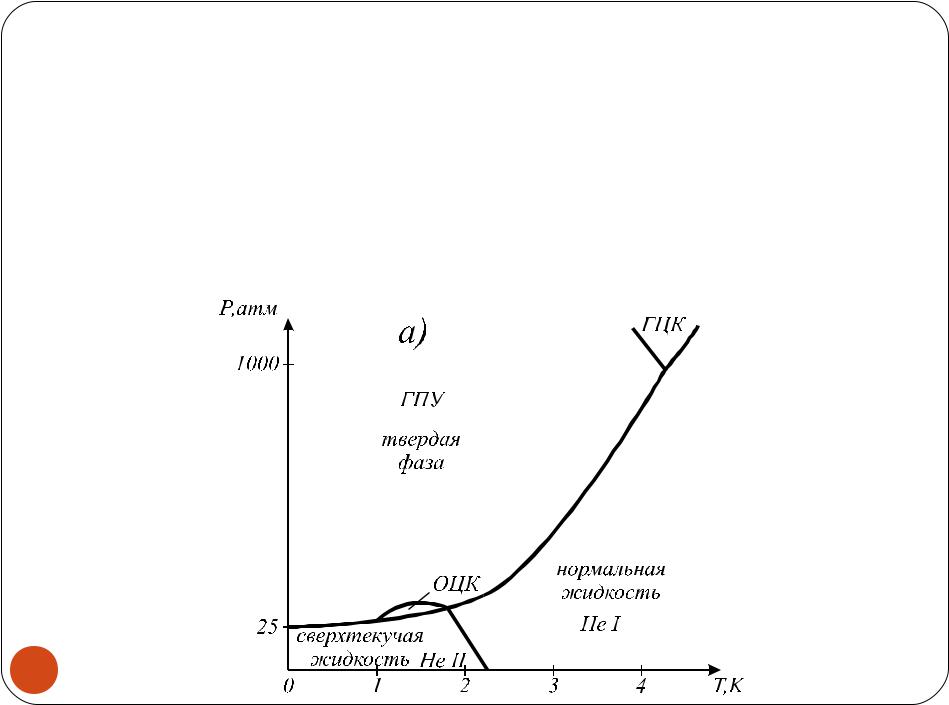
Фазовая диаграмма 4He:
3
Квантовые. кристаллы
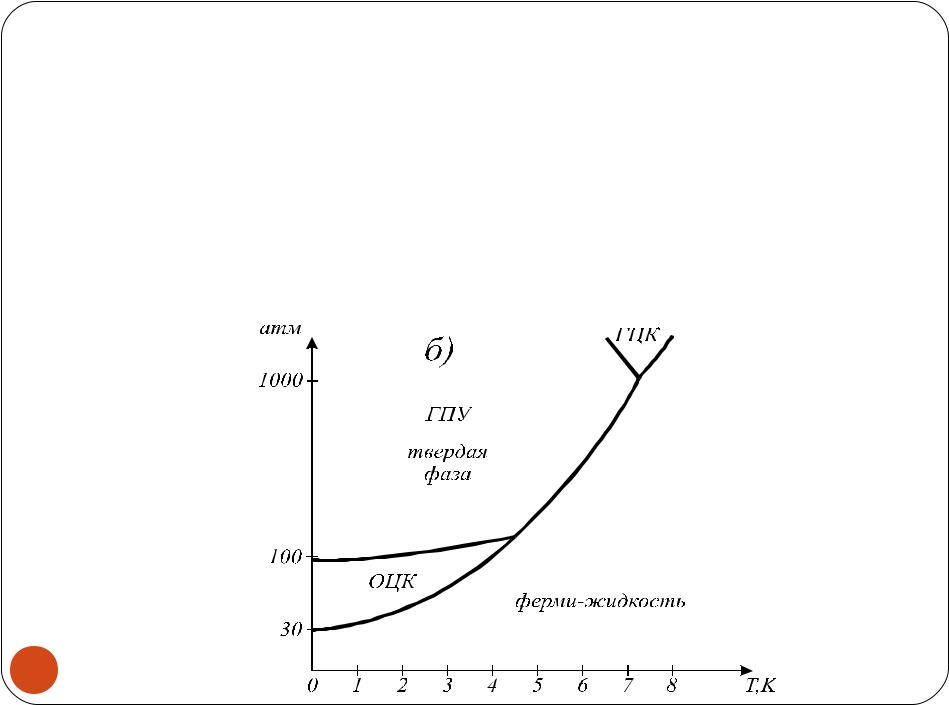
Вследствие малой массы и чрезвычайно слабого взаимодействия атомы гелия находятся в состоянии
достаточно интенсивного нулевого движения и
совершают туннелирование с обменом вдоль
положений равновесия решетки
Фазовая диаграмма 3He:
диаграмма 3He:
4

Квантовые. жидкости
При нормальном давлении оба изотопа гелия – квантовые жидкости даже при нуле температур
Других реальных квантовых жидкостей в природе
нет
Условие квантовости жидкости при конечной
температуре: тепловая длина волны де-Бройля lT
сравнима с межатомнымT /[2 mkрасстояниемBT] ~ a a:
Тепловая длина характеризует амплитуду тепловых колебаний, так что это условие – также оценка температуры, ниже которой возможно наблюдать
квантовое поведение жидкости
Наиболее ярким свойством квантовой жидкости 4He является сверхтекучесть при Tλ <2.17K
5

Квантовые. жидкости
Парное взаимодействие между нейтральными атомами инертного газа хорошо аппроксимируется стандартным потенциалом Леннарда – Джонса («6-
12»): |
|
12 |
|
|
6 |
||
|
V(r) 4 |
|
|
|
|
|
|
|
|
|
|||||
|
r |
r |
|
||||
Газообразная, жидкая и твердая фазы в остальных инертных газах (Ne, Ar, Kr, Xe) неплохо описываются моделью ансамбля классических частиц с таким межчастичным взаимодействием. Однако случай гелия не соответствует обычному классическому описанию
Измерения теплоемкости подтвердили наличие термодинамического фазового перехода второго рода: на температурной зависимости теплоемкости наблюдался излом производной
6
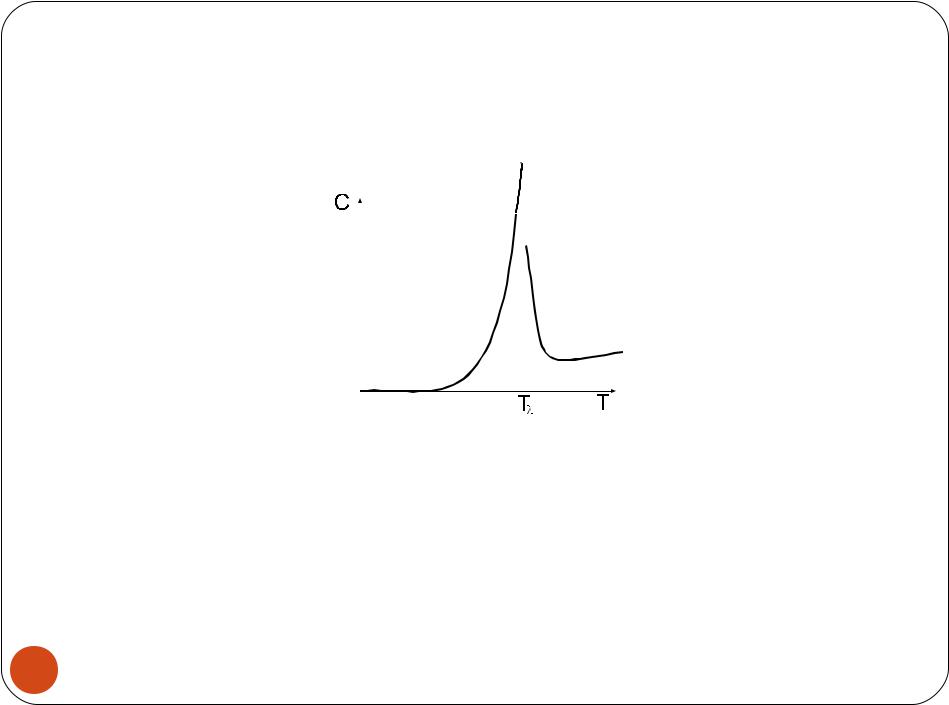
Квантовые. жидкости
Фазу жидкости при температуре ниже Tλ называют
гелий-II в отличие от обычного жидкого гелия при T > Tλ, которую принято называть гелий-I
Наиболее замечательное свойство гелия-II – полное
отсутствие вязкости, т.е. идеальная текучесть
жидкости без трения – сверхтекучесть
7
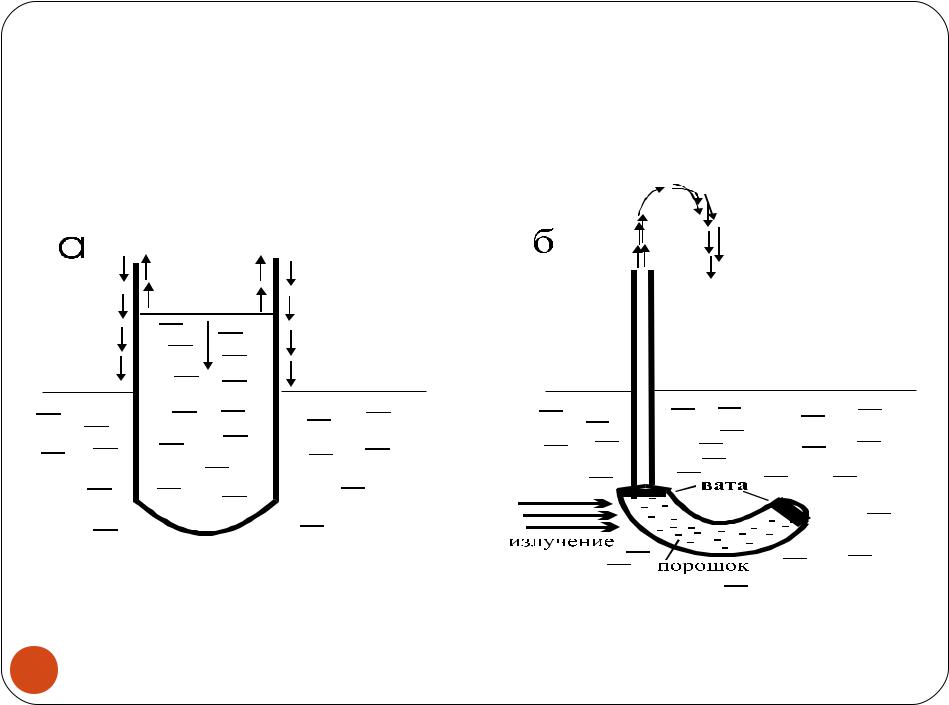
Сверхтекучесть.
Истекание гелия из сосуда
8

Сверхтекучесть.
Сверхтекучесть гелия объясняется нулевой вязкостью
Для объяснения сверхтекучести Ландау предложил
двухжидкостную модель
Жидкий 4He при T<Tλ представляет собой две взаимопроникающие жидкости – нормальную и сверхтекучую компоненты
Для достаточно малых скоростей можно полагать,
что полная плотность |
ρ и полная плотность потока |
s n; |
j svs nv |
j являются суммой вкладов от обеих составляющих:
Для определения температурной зависимости ρs и
доказательства справедливости двухжидкостной
модели был проведен целый ряд экспериментов
9

Сверхтекучесть.
Теория Ландау объясняет, что так как результирующий спин анома 4He равен нулю, и он является бозоном, т.е. подчиняется статистике Бозе- Эйнштейна
Плотность бозе-конденсата, согласно теории, точно совпадает с экспериментальным законом
s / 1 (T / T )3/ 2
Именно конденсатная часть и отождествляется со сверхтекучей жидкостью
Для взаимодействующих атомов гелия, моделируемых как бозе-газ с взаимодействием, рассчитан спектр возбуждений, который состоит из обычных звуковых возбуждений – фононов, и из так называемых ротонов - локализованных вихревых образований. Именно фононы и ротоны слагают нормальную компоненту
10 гелия-II
