1.10. Куперовские пары
Куперовские пары. Энергия связи и радиус. Теория БКШ.
Гамильтониан БКШ. Волновая функция БКШ
Притяжение между частицами.
Основное состояние свободного газа электронов соответствует заполнению всех одноэлектронных
уровней энергии вплоть до некоторой энергии –
энергии Ферми
Такое состояние является неустойчивым при наличии
сколь угодно слабого притяжения между частицами
Рассмотрим систему из двух электронов на фоне электронного газа в системе отсчета, в которой их
центр масс |
системы: |
Согласно принципу
Уравнение
2
Притяжение между частицами.
Уравнение Бете – Голдстоуна:
Если взаимодействие V отвечает притяжению, то
возможны также решения, соответствующие
некоторым связанным состояниям с энергиями E<2EF
Рассмотрим упрощенное взаимодействие:
Уравнение примет вид:
3
Притяжение между частицами.
Условие самосогласованности:
Вводя замену
В пределе малых энергий:
В пределе слабого взаимодействия:
4
Задача о двумерной. яме
Отсутствие порога по взаимодействию подтверждается сопоставлением с задачей о
двумерной потенциальной яме
Найдем энергию связанного состояния в мелкой двумерной потенциальной яме и сравним с энергией
связи электронов в куперовской паре. Энергия
связанного |
|
состояния |
подчиняется |
|
; |
следующему |
|||||
kJ0( a)K0(ka) J0 |
( a)K0 |
(ka); k |
2mE/ |
|
|
||||||
|
|
' |
' |
|
|
|
|
2 |
|
|
|
трансцендентному2 2 |
уравнению: |
|
|
|
|
|
|
||||
k |
|
2mU0 / . |
|
|
|
|
|
|
|
||
E |
2 2 ma2 exp[ 1/(S )]; S 2 a2; |
U N ; |
|||||||||
В случае мелкой ямы имеем:2 |
|
|
|
|
0 |
0 |
|||||
|
|
|
|
|
|
||||||
|
|
|
|
N0 m 2 |
|
|
|
|
|
|
|
5
Пропускание тока через сверхпроводник.
Уравнение для энергии пары:
1/ V kF2 / 4 2 'dqdcos {1/[ 2K2 / 4m E 2kFq 2 / m]};
' 0 2kFq kFKcos 2m D /
Учитывая, что
m D / kFK, m| E| / 2 KkF ,
получаем уравнение на энергию связи:
1 (VN(0) / 2){ln[2 D / | E| 1] 2KkF / m| E|}
В линейном приближении имеем:
| E| | E0 | 2KkF / m
E0 2 D exp[ 2/ VN(0)]
6
Учет кулоновского отталкивания.
Уравнение для фурье-компоненты волновой функции
пары:2 kg(k) [Vkk' VkkC ']g(k') Eg(k);
k'
V |
|
|
V, 0 k , k' D; |
VC |
|
VC, 0 k , k' P; |
|
kk' |
|
|
0, otherwise; |
kk' |
|
|
0, otherwise; |
|
|
|
|
|
|
||
Введем обозначения:' |
'' |
1/[2 k | E|]; |
||
1 |
k1/[2 k |
| E|]; 2 |
k |
|
C1 |
k' g(k); C2 |
k'' g(k); |
|
|
Один штрих соответствует интегрированию по области электрон-фононного взаимодействия, два штриха – по области кулоновкого отталкивания
Получаем:| E| 2 D exp( 2/ ef );
ef N(0)[V VC /{1 (VCN(0) / 2)ln( P / D)}]
7
Теория. БКШ
Волновая функция N электронов:
Фурье-компонента функции пары:
Для полной функции
Введем операторы вторичного квантования с
коммутационными соотношениями
Тогда
8
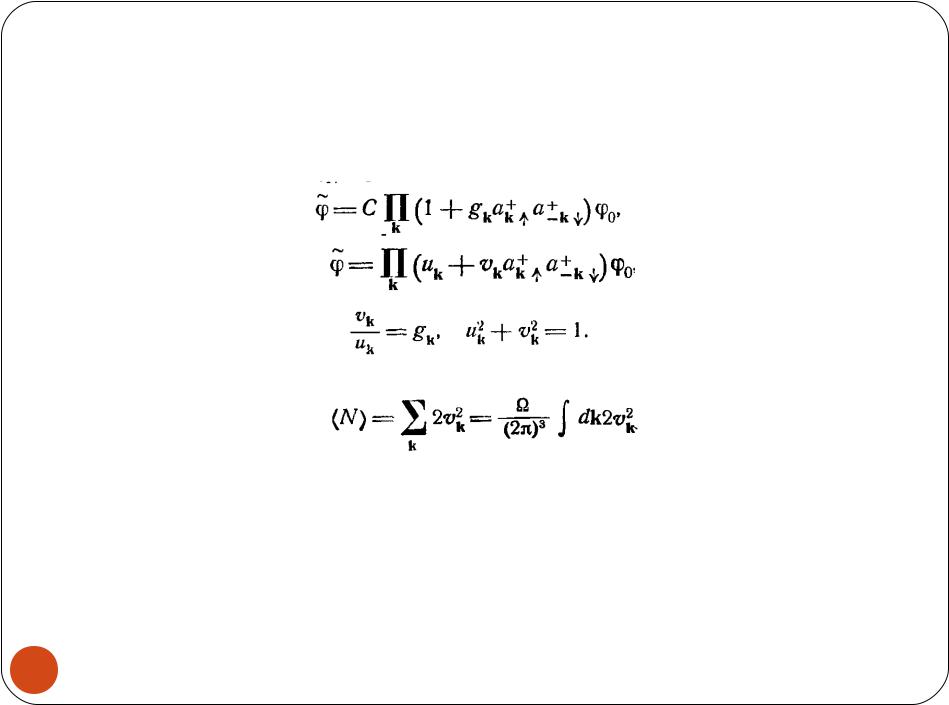
Теория. БКШ
Рассмотрим производящую функцию
Среднее число частиц:
Относительные флуктуации числа частиц очень малы: 
9
Теория. БКШ
Для нахождения энергии основного состояния необходимо минимизировать выражение
Кинетическая энергия:
Потенциальная энергия:
Выражение |
легко |
преобразуется: |
|
|
Члены, отвечающие куперовскому спариванию в |
10 |
потенциальной |