1.7. Зонная теория ферромагнетизма
Спиновый парамагнетизм в теории Стонера. Переход металл – диэлектрик. Модель Хаббарда. Модель Мотта
Приближение сильной связи.
Электрон в твердом теле ведет себя как квазичастица: в отсутствии примесей он не рассеивается, имеет определенный квазиимпульс (не являющийся собственным числом оператора импульса), закон дисперсии, отличный от закона дисперсии свободной частицы и, соответственно, не имеет определенной координаты
Рассмотрим идеальный кристалл в приближении сильной связи. Хорошим квантовым числом в приближении сильной связи электрона с узлом является номер узла. Если ввести узельные операторы рождения и уничтожения электрона на узле, то гамильтониан системы запишется следующим
образом: |
|
0ai ai tijai aj |
|
H |
|||
|
|
i |
i j, |
Первый член описывает “затравочную” (нулевую) энергию электронов, локализованных на узлах; второй член описывает перескоки на соседние узлы
2
Приближение сильной связи.
Перейдем к фурье-представлению:
|
1 |
|
|
|
al |
|
ap exp(ipRl ) |
||
|
|
|||
|
|
|||
|
|
N p |
||
|
1 |
|
|
|
al |
|
ap exp( ipRl ) |
||
|
|
|||
|
|
|||
|
|
N p |
||
Тогда гамильтониан принимает диагональный вид:
|
|
|
|
|
|
|
H |
pap ap ; |
p 0 |
t(| Rl | exp( ipRl) |
|
|
|
p |
|
Rl |
|
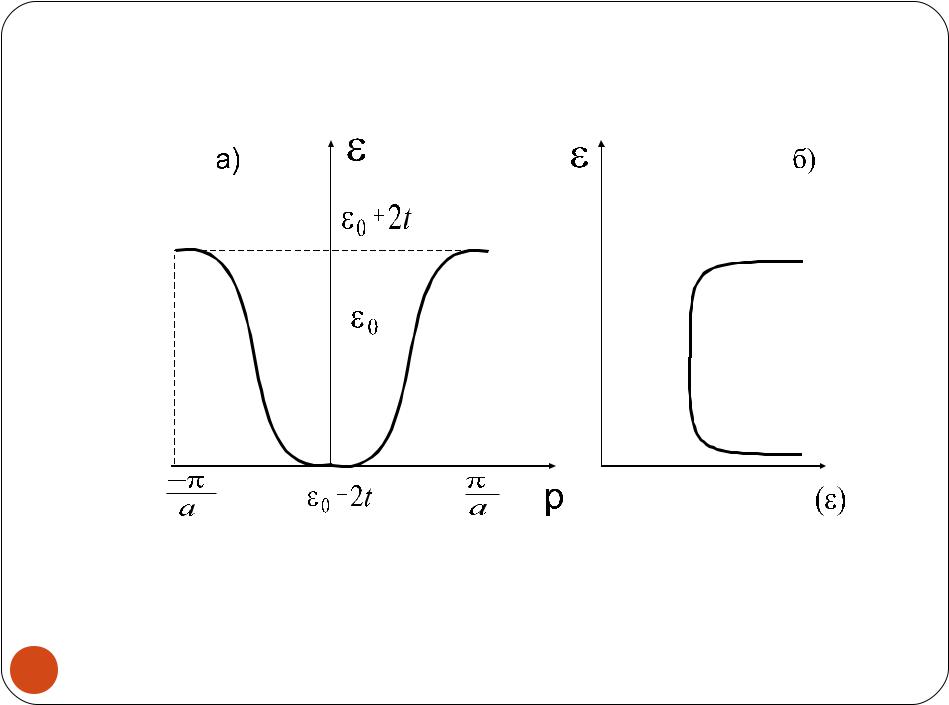
Закон дисперсии электрона с учетом взаимодействия только ближайших соседей
q 0 2t(cosqXa cosqYa cosqZa)
Одномерный случай:
q 0 2t cosqa
Эффективная масса электрона:
m* |
2 |
2ta2 |
|
3 |
|
Приближение сильной связи.
Этот закон дисперсии описывает полосу энергии,
равную 2Zt, так называемую зону проводимости. Ее ширина пропорциональна вероятности перескока. При увеличении концентрации электронов зона может последовательно заполняться в соответствии с принципом Паули.
4
Парамагнетизм. Паули
Рассмотрим газ свободных электронов в слабом магнитном поле. Суммарная энергия электрона будет
зависеть от ориентации его спина относительно
внешнего поля: |
p 0H; |
p |
p 0H |
p |
Суммарный магнитный момент системы есть сумма
магнитных моментов электронов со спином вверх минус магнитный моментM (n nэлектронов) ; со спином вниз:
0
|
n |
|
|
f( |
p |
|
H) 1/ 2 ( )d f( H), |
1. |
||||
|
|
|
|
|
0 |
|
|
|
0 |
|
||
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
Для малых полей |
0H d ( )( |
f |
) |
|
|||||||
|
|
|
|
|
M |
|
|
|||||
При низких температурах2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
M |
0H (Ef ); |
|
|
||
5 |
|
|
|
|
|
|
02 (Ef ). |
|
|
|||
Ферромагнетизм в модели Стонера.
Рассмотрим газ делокализованных электронов с кулоновским взаимодействием
V 1/ 2 V(q)
ap q, ap' q, 'ap' 'ap 
pp'q '
В приближении среднего поля:
V 1/ 2 V(q){ ap q, ap ap' q, 'ap' ' ap q, ap' ' ap' q, 'ap } pp'q '
1/ 2 (V(0) V(| p p'| ')fp fp' '.
pp' '
Газ можно рассматривать как свободный с законом
дисперсии |
|
|
|
p p 1/ N |
(V(0) |
V(| p p'| ')fp' ' |
|
p' ' |
|
|
|
6
Ферромагнетизм в модели Стонера.
Кулоновское взаимодействие сильно экранировано, и поэтому при малых импульсах можно пренебречь
|
зависимостью матричного элемента от импульса: |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
V(| q|) |
|
4 e |
|
4 e |
|
V cons |
|
||||||||
|
|
|
|
|
q2 k02 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
k02 |
|
|
|
|
|
|
|||
|
Окончательно, |
|
|
|
|
|
V / N fp' |
|
|
|
|
|
|
|||||||
|
|
|
|
|
p |
p |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
p' |
|
|
|
|
|
|
|
|
Средняя намагниченность системы: |
|
|
|
|
|||||||||||||||
|
R |
1 {N |
N }, N |
fp , N N |
|
N . |
|
|
|
|||||||||||
|
|
|
|
N |
|
|
|
|
|
|
|
p |
|
|
|
|
|
Стонера |
для |
|
|
Самосогласованное |
|
|
|
уравнение |
|
|
|||||||||||||
|
намагниченности электронного газа с кулоновским |
|||||||||||||||||||
|
взаимодействием: |
|
VR |
|
|
|
VR |
|
|
|
|
|||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
R |
|
|
|
, p |
, |
|
|
|
, f , p , |
|
|
|
|
|
|||||
|
|
f |
2 |
|
|
2 |
, , |
|
||||||||||||
|
|
N p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
7 |
f , p, x, |
{exp[( p x )] 1} 1. |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ферромагнетизм в модели Стонера.
Нормировка на число частиц: |
|||
N |
1 |
|
|
exp ( p ) 1 |
|||
p |
|||
Исследуем в общем случае условия существования
фазового перехода. При разложении до первой производной фермиевской функции распределения
по энергии имеем: V fp
1 N p p
При низких температурах1 V ( )
Разложим уравнение Стонера до третьей
производной функции распределения по энергии: |
||||||||||
|
V |
|
fp |
|
3 |
2 |
|
|
3 |
|
|
|
|
V R |
|
|
|
fp |
|||
1 |
|
( |
|
) |
|
|
( |
|
) |
|
|
|
24 |
|
|
||||||
|
p |
|
3 |
|||||||
|
N p |
|
p |
p |
||||||
8
Ферромагнетизм в модели Стонера.
В наиболее существенной области интегрирования ε~μ
и |
|
1 |
(1 |
2 |
|
]) |
|
||
|
3fp |
|
2sh [ |
2T |
0 |
||||
|
3 |
8T3 |
|
|
4 |
|
|||
|
p |
|
|
|
|
ch [ 2T ] |
|
|
|
|
|
|
|
|
|
|
|
|
|
Условие Блоха – Стонера для существования при ненулевой температуре спонтанной намагниченности:
| V fp | 1
N p p
Условие на параметр2 взаимодействия при низких температурах: V 3Ef
Ферромагнетизм Стонера возникает только при достаточно большом параметре кулоновского
9взаимодействия
Модель . Хаббарда
Гамильтониан |
|
|
ферми-газа |
с |
a |
|
кулоновским |
||||||||||
взаимодействием:H a a 1/ 2 |
V |
a |
|
a |
a . |
||||||||||||
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
, ' p2 ' ' p1' |
||
|
|
p, p |
|
|
|
|
|
|
p1p2p1'p2 ' p1 , |
p2 |
|||||||
|
p |
|
|
|
|
|
|
p1p2p1 / p2 ' ' |
|
|
|
|
|
||||
Хорошим |
квантовым |
числом |
является |
|
номер узла. |
||||||||||||
Перейдем |
от |
импульсного представления |
к |
узельным |
|||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
операторам: |
|
ap |
|
|
|
ai exp{ip ri } |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
N |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|||
Кинетическая
tij 1 p
N p
|
|
kin |
tijai aj , |
|
|
|
H |
имеет вид: |
|||||
часть гамильтонианаi j, |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| aB ). |
exp(ip[ ri rj ]) ~ exp( | ri |
rj |
|||||
Амплитуда перескока быстро затухает в узкозонном веществе с сильно локализованными носителями, и
|
обычно достаточно учесть перескоки только на |
10 |
ближайшие соседи |