

22.2.Линейные однородные уравнения
счастными производными первого порядка
ОПРЕДЕЛЕНИЕ. Линейным однородным уравнением с частными производными первого порядка3 называется уравнение вида
F1(x1,K, xn ) |
∂z |
+K+ Fn (x1,K, xn ) |
∂z |
= 0, |
(22.5) |
|
∂x |
∂x |
n |
||||
|
1 |
|
|
|
|
|
где Fi (x1,K, xn ) – заданные функции, непрерывно дифференцируемые в рассматриваемой области G n, z = z(x1,K, xn ) – неизвестная функция.
Запишемсистемуобыкновенныхдифференциальныхуравненийвида:
|
dx1 |
= |
|
dx2 |
=K= |
dxn |
. |
(22.6) |
|
|
F1 (x1,K, xn ) |
F2 |
(x1,K, xn ) |
Fn (x1 |
,K, xn ) |
||||
|
|
|
|
|
|||||
Ее называют соответствующей уравнению (22.5). Связь между уравнением (22.5) и системой обыкновенных уравнений (22.6) устанавливает следующая теорема.
ТЕОРЕМА 22.1. Функция z =ϕ(x1,K, xn ) является решением уравне-
ния (22.5) тогда и только тогда, когда ϕ(x1,K, xn ) = C является первым интегралом системы (22.6).
ДОКАЗАТЕЛЬСТВО. 1) Достаточность ( ). Пусть имеется уравнение
ϕ(x1, x2 ,K, xn+1 ) = C . |
(22.7) |
Очевидно, что уравнение (22.7) определяет первый интеграл системы (22.6) тогда и только тогда, когда для любого ее решения x1,K, xn+1
|
|
|
|
|
|
|
ϕ(x1, x2 ,K, xn+1 ) ≡ C . |
|
|
|||||||||||||||
Отсюда |
|
|
|
|
|
∂ϕ |
dϕ(x1, x2 ,K, xn+1) ≡ 0 ; |
|
|
|||||||||||||||
|
|
|
|
|
|
|
∂ϕ |
|
|
|
|
|
|
|
|
∂ϕ |
|
|
|
|
||||
|
|
|
|
|
|
dx1 + |
|
|
dx2 |
+K+ |
|
|
|
|
|
dxn+1 ≡ 0 . |
|
|||||||
|
|
|
|
|
∂x |
∂x |
2 |
|
∂x |
|
|
|
||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
n+1 |
|
|
||||
Но из (22.6) находим: |
dxi = kFi (x1,K, xn+1 ) . |
|
|
|||||||||||||||||||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
∂ϕ |
|
|
|
|
|
|
|
|
|
∂ϕ |
|
|
|
|
|
|
|
≡ 0 , |
|||||
k |
|
|
F1 |
(x1,K, xn+1) +K+ |
|
|
|
|
|
|
Fn+1 |
(x1 |
,K, xn+1) |
|||||||||||
∂x |
|
∂x |
n+1 |
|||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
∂ϕ |
F1(x1,K, xn+1) +K+ |
∂ϕ |
|
|
Fn+1(x1,K, xn+1) ≡ 0 . (22.8) |
|||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
∂x |
∂x |
|
|
|
|
||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
n+1 |
|
|
|
|
|
||||||
3 или «линейным однороднымуравнением вчастных производных первого порядка»
181

Таким образом, функция
z =ϕ(x1,K, xn )
является решение уравнения (22.5).
2) Необходимость ( ). Легко проверить, что условие (22.8) является не только необходимым, но и достаточным условием того, что уравнение ϕ(x1, x2 ,K, xn+1 ) = C определяет первый интеграл системы диф-
ференциальных уравнений (22.6). Следовательно, если z =ϕ(x1,K, xn ) – решение уравнения (22.5), то уравнение ϕ(x1,K, xn ) = C определяет первый интеграл системы (22.6).
Пусть найдена система независимых4 первых интегралов системы дифференциальных уравнений (22.15), образующих ее общий интеграл:
|
ϕ1 (x1,K, xn ) = C1 , |
||||||||
|
ϕ |
2 |
(x ,K, x |
n |
) = C |
2 |
, |
|
|
|
|
1 |
|
|
|
|
|||
|
KKKKKKK |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
ϕn−1 (x1,K, xn ) = Cn−1 . |
|||||||||
По теореме 22.1 функции ϕi (x1,K, xn ) |
(i = |
|
) являются решениями |
||||||
1, n −1 |
|||||||||
уравнения (22.5), причем справедлива следующая теорема.
ТЕОРЕМА 22.2. Если ϕi (x1,K, xn ) = Ci (i =1, n −1) – независимые пер-
вые интегралы системы (22.6) и Φ – произвольная непрерывно дифференцируемая функция n −1 аргумента, то z = Φ(ϕ1,K,ϕn−1 ) – общее
решение уравнения (22.5).
ПРИМЕР 22.1. Найти общее решение уравнения x ∂∂ux + y ∂∂uy + z ∂∂uz = 0 .
РЕШЕНИЕ. Данное уравнение – линейное однородное. Искомая функция u = u(x, y, z) . Соответствующая система обыкновенных дифферен-
циальных уравнений имеет вид
dxx = dyy = dzz .
Из равенства первой и третьей дроби получим один первый интеграл системы:
dxx = dzz ,
4 т. е. ни один из них не следует из остальных.
182

ln |
|
z |
|
|
= ln |
|
x |
|
+ ln C1 |
|
|
или |
z |
|
= C1 . |
||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
x |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из равенства второй и третьей дроби получим другой первый инте- |
|||||||||||||||||||||||||||
грал системы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
= dz |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
z |
|
|
|
|
|
|
|
ln |
|
z |
|
|
= ln |
|
|
|
|
y |
|
+ ln C2 |
|
|
или |
z |
|
= C2 . |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
y |
|
||||||||||||||||
Первые интегралы |
|
|
z |
= C |
|
и |
z |
= C |
|
|
|
|
|
||||||||||||||
|
|
|
2 |
независимы и образуют общий |
|||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
x |
1 |
|
|
|
|
|
y |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
интеграл системы дифференциальных уравнений. Следовательно, общее решение однородного дифференциального уравнения в частных производных имеет вид
|
|
z |
|
|
u = Φ |
z |
; |
. |
|
|
|
|||
x |
|
y |
||
Теперь покажем, как найти решение задачи Коши для линейного однородного уравнения с частными производными первого порядка.
Пусть дано уравнение
F |
(x ,K, x |
|
) |
∂z |
+K+ F |
(x ,K, x |
|
) |
∂z |
= 0 , |
(22.5) |
|
|
∂x |
|
∂x |
|
||||||||
1 |
1 |
n |
|
n |
1 |
n |
|
n |
|
|
||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
где Fi (x1,K, xn ) – заданные функции, непрерывно дифференцируемые в рассматриваемой области G n, z = z(x1,K, xn ) – неизвестная функ-
ция. Требуется найти его решение, удовлетворяющее условию z(x1,K, xn−1, xn = xn0 ) = Φ0 (x1,K, xn−1 ) ,
где Φ0 (x1,K, xn−1 ) – заданная функция n −1 аргумента.
Найдем систему независимых первых интегралов системы дифференциальных уравнений (22.6), образующих ее общий интеграл:
|
|
ϕ1 (x1,K, xn ) = C1 , |
|
|
|||||||||
|
|
ϕ |
2 |
(x ,K, x |
) = C |
, |
|
|
|||||
|
|
|
1 |
|
n |
|
2 |
|
|
|
|
||
|
|
KKKKKKK |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Обозначим |
ϕn−1 (x1,K, xn ) = Cn−1 . |
|
|||||||||||
ϕ1 (x1,K, xn−1, xn0 ) = |
ϕ1 , |
|
|||||||||||
|
|
||||||||||||
|
ϕ |
(x ,K, x |
n−1 |
, x |
n0 |
) = |
ϕ |
|
, |
(22.9) |
|||
|
2 |
1 |
|
|
|
2 |
|
||||||
|
|
KKKKKKK |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x1,K, xn−1, xn0 ) =ϕn−1 . |
|
|||||||||||
ϕn−1 |
|
||||||||||||
183

Разрешим (22.9) относительно x1,K, xn−1 (это всегда можно сделать в окрестности точки M 0 (x10 , x20 K, xn0 ) , такой что Fi (M 0 ) ≠ 0 ). Получим:
|
x1 = ω1 ( |
ϕ1, |
ϕ |
2 ,K, |
ϕ |
n−1 ) , |
|
||||||||||
|
x2 = ω2 ( |
ϕ1, |
ϕ |
2 ,K, |
ϕ |
n−1 ) , |
(22.10) |
||||||||||
|
KKKKKKKKKK |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn−1 = ωn−1 (ϕ1,ϕ2 ,K,ϕn−1 ). |
|
||||||||||||||||
Тогда решение уравнения (22.5), удовлетворяющее условию z(x1,K, xn−1, xn = xn0 ) = Φ0 (x1,K, xn−1 ) ,
будет иметь вид
z = Φ0 [ω1 (ϕ1 ,K,ϕn−1 ),ω2 (ϕ1 ,K,ϕn−1 ),K,ωn−1 (ϕ1 ,K,ϕn−1 )]. (22.11)
Действительно, в силу теоремы 2, функция (22.11) определяет решение уравнения (22.5). А при xn = xn0 имеем
z(x1,K, xn−1, xn = xn0 ) =
|
Φ0 (ω1 (ϕ1,K,ϕn−1 ),K,ωn−1 (ϕ1,K,ϕn−1 )) |
|
xn =xn0 |
= |
|
|
|
|
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
= Φ0 ω1 |
(ϕ1 |
|
xn =xn0 |
,K,ϕn−1 |
|
xn =xn0 ),K,ωn−1(ϕ1 |
|
xn |
=xn0 |
,K,ϕn−1 |
|
xn =xn0 ) = |
|||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
14243 |
14243 |
|
|
|
14243 |
|
|
|
|
14243 |
|
|||||||||||||||||||||
|
|
|
ϕ1 |
|
|
|
|
ϕ |
n−1 |
|
|
|
|
|
|
|
|
ϕ1 |
|
|
|
|
|
|
|
|
|
ϕ |
n−1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
= Φ |
0 |
|
ω ( |
ϕ |
,K, |
ϕ |
n−1 |
),K,ω |
n−1 |
( |
ϕ |
,K, |
ϕ |
n |
|
−1 |
) |
= |
|
|
|
|
|
|||||||
|
|
|
|
|
|
1442443 |
14424443 |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
xn−1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
= Φ0 (x1,K, xn−1 ) .
Замечание. Алгоритм нахождения решения задачи Коши показывает, что решение начальными данными определяется однозначно.
ПРИМЕР 22.2. Найти решение уравнения x |
∂u |
+ y |
∂u |
+ |
z |
∂u |
= 0 , |
∂x |
∂y |
|
|||||
|
|
|
2 ∂z |
|
|||
удовлетворяющее начальному условию u(1, y, z) = y + z2 .
РЕШЕНИЕ. 1) Данное уравнение – линейное однородное. Искомая функция u = u(x, y, z) . Соответствующая система обыкновенных диф-
ференциальных уравнений имеет вид
dxx = dyy = zdz2 .
Изравенства1-йи3-йдробиполучимодинпервыйинтегралсистемы: dxx = 2dzz ,
184
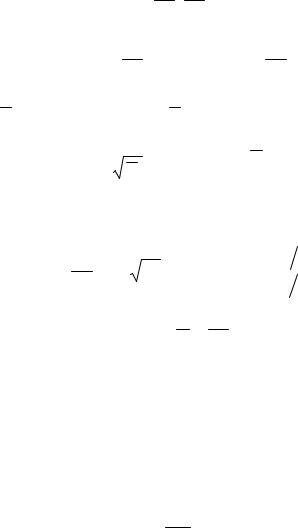
2ln |
|
|
z |
|
= ln |
|
x |
|
+ ln C1 |
или |
|
z2 |
|
= C1 . |
||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
x |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из равенства 2-й и 3-й дроби получим другой первый интеграл: |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
= 2dz |
, |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
z |
|
|
|
|
|
|
2ln |
|
|
z |
|
|
|
= ln |
|
y |
|
+ ln C2 |
или |
|
z2 |
|
= C2 . |
||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
y |
|
||||||||||||||||||
|
z2 |
|
|
= C и |
z2 |
= C |
|
|
|
|
|
|||||||||||||||
Первые интегралы |
|
|
2 |
независимы и образуют общий |
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
x |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
интеграл системы дифференциальных уравнений. Следовательно, общее решение линейного однородного дифференциального уравнения в частных производных имеет вид
u= Φ zx2 ; zy2 .
2)Имеем: ϕ1(x, y, z) = zx2 , ϕ2 (x, y, z) = zy2 .
Тогда |
|
ϕ |
=ϕ (1, y, z) = z2 |
, |
ϕ |
2 |
=ϕ |
2 |
(1, y, z) = |
z2 |
. |
||||||
|
|
||||||||||||||||
|
1 |
1 |
|
|
|
|
|
|
|
|
|
y |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
z = ± ϕ1 , |
|
|
|
|
z2 |
|
|
ϕ |
|
||||
|
|
|
|
|
y = |
|
|
|
= |
|
|
1 . |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
ϕ |
2 |
ϕ |
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Подставляя найденные выражения для y и z в начальное условие и «теряя черточки», получаем искомое частное решение:
u(x, y, z) = |
ϕ1 + (± ϕ |
)2 = |
ϕ1 +ϕ = |
z2 |
x |
+ |
z2 |
, |
|
|
|
|
|||||||
|
1 |
|
ϕ2 |
1 |
z2 |
y |
|
x |
|
|
ϕ2 |
|
|
|
|||||
u(x, y, z) = y + z2 .
xx
ПРИМЕР 22.3. Найти решение уравнения y ∂∂xz − x ∂∂yz = 0 , удовле-
творяющее начальному условию z(x,0) = x −1.
РЕШЕНИЕ. 1) Данное уравнение – линейное однородное. Искомая функция z = z(x, y) . Соответствующая система обыкновенных диффе-
ренциальных уравнений имеет вид
dxy = −dyx .
185

Она имеет единственный первый интеграл (общий интеграл дифференциального уравнения):
|
|
|
|
− xdx = ydy , |
|
y2 |
= − |
x2 |
+C или y2 + x2 = C . |
2 |
|
|||
|
2 |
|
||
Следовательно, общее решение дифференциального уравнения в частных производных имеет вид
z= Φ(y2 + x2 ).
Сгеометрической точки зрения, общее решение представляет собой всевозможные поверхности вращения с осью Oz .
2) Имеем: |
ϕ(x, y) = y2 + x2 . |
|
Тогда |
ϕ |
=ϕ(x,0) = x2 , |
|
x = ± ϕ . |
|
Подставляя найденное выражения для x в начальное условие и «теряя черточку», получаем искомое частное решение:
z(x, y) = ± ϕ −1 = ± x2 + y2 −1.
С геометрической точки зрения, это частное решение представляет собой конус (z +1)2 = x2 + y2 , т.е. поверхность вращения, проходящую
через прямую |
|
|
y = 0, |
|
|
|
−1. |
|
z = x |
|
|
22.3.Линейные неоднородные уравнения
счастными производными первого порядка
ОПРЕДЕЛЕНИЕ. Линейным неоднородным уравнением с частными производными первого порядка называется уравнение вида
F |
(x ,K, x |
n |
, z) |
∂z |
+K+ F |
(x ,K, x |
n |
, z) |
∂z |
= P(x ,K, x |
n |
, z) , (22.12) |
|
|
|||||||||||
1 |
1 |
|
∂x1 |
n |
1 |
|
∂xn |
1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
где Fi (x1,K, xn , z) , P(x1,K, xn , z) – заданные функции, непрерывно дифференцируемые в рассматриваемой области G n+1, z = z(x1,K, xn ) –
неизвестная функция.
Интегрирование уравнения (22.12) сводится к интегрированию некоторого линейного однородного уравнения с частными производными первого порядка. Действительно, предположим, что уравнение
u(x1,K, xn , z) = 0 |
(22.13) |
задает в неявном виде решение уравнения (22.12). Тогда
186
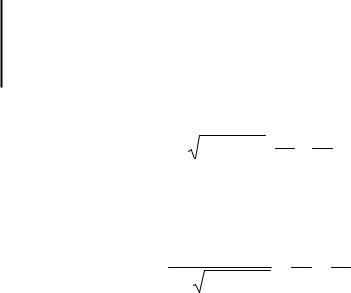
|
|
|
|
|
|
|
|
|
|
∂z |
= − |
u′x |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂xi |
u′z |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
и из уравнения (22.12) находим: |
|
|
|
|
|
|
u′x |
|
|
|
|
||||||||||
|
|
|
|
u′x |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|||
|
|
|
− |
|
1 |
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
F1(x1,K, xn , z) |
u′z |
|
+K+ Fn (x1,K, xn , z) |
|
|
= P(x1,K, xn , z) , |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u′z |
|
|
|||||
F1(x1,K, xn , z) (−u′x |
)+K+ Fn (x1,K, xn , z) (−u′x |
) |
= P(x1,K, xn , z) u′z . |
||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
F (x ,K, x , z) |
∂u |
|
+K+F (x ,K, x , z) |
∂u |
+P(x ,K, x , z) ∂u |
=0 . (22.14) |
|||||||||||||||
|
|
||||||||||||||||||||
1 1 |
n |
∂x1 |
|
|
|
|
n |
1 |
|
n |
|
∂xn |
1 |
|
|
n |
∂z |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Уравнение (22.14) – линейное однородное первого порядка, в котором искомая функция u зависит от n +1 переменной x1,K, xn , z . Соот-
ветствующая ему система дифференциальных уравнений
dx1 |
|
|
=K= |
dxn |
|
|
= |
dz |
|
|
(22.15) |
F (x ,K, x |
n |
, z) |
F (x ,K, x |
n |
, z) |
P(x ,K, x |
n |
, u) |
|||
1 1 |
|
|
n 1 |
|
|
1 |
|
|
имеет n независимых первых интегралов
ϕ1 (x1 ,K, xn , z) = C1 , …, ϕn (x1 ,K, xn , z) = Cn
и, следовательно, общее решение уравнения (22.14) будет иметь вид u = Φ(ϕ1 ,K,ϕn ) .
Но тогда уравнение Φ(ϕ1 ,K,ϕn ) = 0 будет определять в неявном виде общее решение (22.12).
Замечание. На практике, при интегрировании линейных неоднородных уравнений с частными производными первого порядка, уравнение (22.14) обычно не записывают. Записывают сразу его соответствующую систему (22.15).
ПРИМЕР 22.4. Найти общее решение уравнения
(1 + z − x − y) ∂∂xz + ∂∂yz = 2 .
РЕШЕНИЕ. Данное уравнение – линейное неоднородное. Искомая функция z = z(x, y) . Соответствующая система обыкновенных диффе-
ренциальных уравнений имеет вид
dx |
= dy |
= dz . |
1 + z − x − y |
1 |
2 |
Из равенства 2-й и 3-й дроби получим один первый интеграл системы: dy1 = dz2 ,
0,5z = y + C1 или z − 2 y = C1.
187

Другой первый интеграл системы получим, используя свойства равных дробей:
dy |
= |
|
dz − dx − dy |
, |
1 |
2 |
− (1 + z − x − y ) −1 |
||
|
dy |
= d(z − x − y) |
, |
|
|
|
1 |
z − x − y |
|
y − 2 z − x − y = C2 .
z − x − y = C2 .
Первые интегралы z − 2 y = C1 и y − 2 z − x − y = C2 независимы и образуют общий интеграл системы дифференциальных уравнений. Следовательно, общее решение неоднородного дифференциального уравнения в частных производных имеет вид
z − x − y = C2 независимы и образуют общий интеграл системы дифференциальных уравнений. Следовательно, общее решение неоднородного дифференциального уравнения в частных производных имеет вид
Φ(z − 2 y; y − 2 z − x − y )= 0 .
ПРИМЕР 22.5. Найти решение уравнения |
x |
∂z |
− 2 y |
∂z |
= x2 + y2 , |
|
|
∂x |
|
∂y |
|
удовлетворяющее начальному условию z(x,1) = x2 .
РЕШЕНИЕ. 1) Данное уравнение – линейное неоднородное. Искомая функция z = z(x, y) . Соответствующая система обыкновенных диффе-
ренциальных уравнений имеет вид
dxx = −dy2 y = x2 dz+ y2 .
Из равенства 1-й и 2-й дроби получим один первый интеграл системы:
|
|
|
|
|
|
|
dx = |
dy |
, |
|
||
|
|
|
|
|
|
|
− 2 y |
|
||||
|
|
|
|
|
|
|
x |
|
|
|||
|
|
|
|
|
2 dx |
= − dy |
, |
|||||
|
|
|
|
|
|
|
|
|
x |
|
y |
|
2ln |
|
x |
|
= −ln |
|
y |
|
+ ln C1 |
или x2 y = C1 . |
|||
|
|
|
|
|||||||||
Другой первый интеграл системы получим, используя свойства равных дробей:
xdx = − 0,5ydy |
= |
|
dz |
|
, |
||
x2 |
y2 |
|
x2 + y2 |
|
|
||
|
xdx − 0,5 ydy |
= |
|
dz |
|
, |
|
x2 + y2 |
|
x2 + y2 |
|
||||
|
|
|
|
|
|||
188

|
x2 |
|
y2 |
|
|
|
|
+ |
|
|
= 0 , |
|
|
||||
xdx −0,5ydy = dz или d z − |
2 |
4 |
|
||
|
|
|
|
z − |
x2 |
+ |
y2 |
|
= C2 . |
|
|
|
|||
|
|
|
|
|
|
||||||
2 |
4 |
|
|
|
|
|
|
|
|||
Первые интегралы x2 y = C и |
z − |
x2 |
|
+ |
y2 |
= C |
2 |
независимы и обра- |
|||
|
|
|
|||||||||
1 |
|
2 |
4 |
|
|
||||||
|
|
|
|
|
|||||||
зуют общий интеграл системы дифференциальных уравнений. Следовательно, общее решение неоднородного дифференциального уравнения в частных производных имеет вид
Φ x2 y; z − x22 + y42 = 0 .
Разрешая это уравнение относительно второй переменной, получим общее решение неоднородного уравнения в явном виде:
|
|
|
|
|
|
z − |
x2 |
|
|
+ |
|
y2 |
|
|
= f (x2 y) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
x2 |
|
|
|
|
y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
z = f |
(x2 y) + |
|
− |
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2) Найдем искомое частное решение. Имеем: |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
ϕ (x, y, z) = x2 y , |
|
|
|
|
|
ϕ |
2 |
|
(x, y, z) = z − |
x2 |
+ |
y2 |
. |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
4 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
||||||||
Тогда |
|
ϕ |
=ϕ (x,1, z) = x2 , |
|
|
|
|
|
ϕ |
2 |
|
=ϕ |
2 |
(x,1, z) = z − |
|
+ 1 . |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
4 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
x = ± ϕ1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
ϕ |
|
|
|
|
1 |
|
||||||||||||
|
|
|
|
|
|
|
|
z = |
ϕ |
2 + |
|
|
|
|
|
|
− |
|
|
|
= |
ϕ |
2 + |
|
1 − |
|
. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
4 |
|
4 |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
z в |
2 |
|
|
|
|
|||||||||||||||
Подставляя |
найденные выражения |
|
|
для |
|
|
|
|
|
и |
|
начальное условие |
|||||||||||||||||||||||||||||||||||||||||
z(x,1) = x2 и «теряя черточки», получаем искомое частное решение: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
ϕ |
2 |
+ ϕ1 − 1 = (± ϕ |
)2 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− ϕ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
ϕ |
2 |
+ ϕ1 − 1 =ϕ |
|
|
или |
|
ϕ |
2 |
|
− 1 = 0 |
, |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
4 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
z − |
|
x2 |
|
+ |
|
|
y2 |
|
− |
x2 y |
|
− |
1 |
= 0 , |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
4 |
|
|
2 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
z = |
|
x2 |
|
|
|
|
|
|
y2 |
|
x2 y |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
+ |
|
|
. |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
4 |
|
|
|
2 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
189
СПИСОК ЛИТЕРАТУРЫ
1.Краснов М.Л. Обыкновенные дифференциальные уравнения: учебное пособие / Краснов М. Л. – М.: Высшая школа, 1983. – 128 с.
2.Краснов М.Л. Сборник задач по обыкновенным дифференциальным уравнениям: учебное пособие / Краснов М. Л., Киселев А. И., Макаренко Г. И. – 3-е изд., перераб. и доп. – М.: Высшая школа, 1978. – 287 с.
3.Филиппов А.Ф. Сборник задач по дифференциальным уравнениям : учебное пособие / Филиппов А. Ф. – 2-е изд. – М.: Изд-во ЛКИ, 2008. – 240 с.
4.Степанов В. В. Курс дифференциальных уравнений: учебник для вузов / Степанов В. В. – 9-е изд., стер. – М.: Едиториал УРСС, 2004. – 472 с.
5.Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных уравнений: учебник / Матвеев Н. М. – 3-е изд., испр. и доп. – М.: Высшая школа, 1967. – 564 с.
6.Барышева В.К. Обыкновенные дифференциальные уравнения (часть 1, 2): учебное пособие / Барышева В.К., Ивлев Е.Т., Имас О.Н., Пахомова Е.Г. – Томск: Изд-во ТПУ, 2003. – 112 с.
190
