
кафедра физики-Методические указания к РГР
.pdf21
Окончание таблицы №1
7 |
1.71 |
1.72 |
1.73 |
1.74 |
1.75 |
1.76 |
1.77 |
1.78 |
1.79 |
1.80 |
|
1.171 |
1.172 |
1.173 |
1.174 |
1.175 |
1.176 |
1.177 |
1.178 |
1.179 |
1.180 |
|
1.271 |
1.272 |
1.273 |
1.274 |
1.275 |
1.276 |
1.277 |
1.278 |
1.279 |
1.280 |
|
2.71 |
2.72 |
2.73 |
2.74 |
2.75 |
2.76 |
2.77 |
2.78 |
2.79 |
2.80 |
|
2.59 |
2.58 |
2.57 |
2.56 |
2.55 |
2.54 |
2.53 |
2.52 |
2.51 |
2.50 |
8 |
1.81 |
1.82 |
1.83 |
1.84 |
1.85 |
1.86 |
1.87 |
1.88 |
1.89 |
1.90 |
|
1.181 |
1.182 |
1.183 |
1.184 |
1.185 |
1.186 |
1.187 |
1.188 |
1.189 |
1.190 |
|
1.281 |
1.282 |
1.283 |
1.284 |
1.285 |
1.284 |
1.283 |
1.282 |
1.281 |
1.280 |
|
2.81 |
2.82 |
2.83 |
2.84 |
2.85 |
2.86 |
2.87 |
2.88 |
2.89 |
2.90 |
|
2.49 |
2.48 |
2.47 |
2.46 |
2.45 |
2.44 |
2.43 |
2.42 |
2.41 |
2.40 |
9 |
1.91 |
1.92 |
1.93 |
1.94 |
1.95 |
1.96 |
1.97 |
1.98 |
1.99 |
1.100 |
|
1.191 |
1.192 |
1.193 |
1.194 |
1.195 |
1.196 |
1.197 |
1.198 |
1.199 |
1.200 |
|
1.279 |
1.278 |
1.277 |
1.276 |
1.275 |
1.274 |
1.273 |
1.272 |
1.271 |
1.270 |
|
2.91 |
2.92 |
2.93 |
2.94 |
2.95 |
2.96 |
2.97 |
2.98 |
2.99 |
2.100 |
|
2.39 |
2.38 |
2.37 |
2.36 |
2.35 |
2.34 |
2.33 |
2.32 |
2.31 |
2.30 |
5 ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ РГР 2
«Электростатика. Постоянный электрический ток. Магнитное поле. Электромагнитная индукция»
Задача1. На шелковой нити в воздухе подвешен маленький положительно заряженный шарик массой m=90 мг. Если ниже шарика на расстоянии r=1 см от него поместить равный, но отрицательный заряд, то сила натяжения нити увеличится в 3 раза. Определить заряд шарика.
Дано:
m=90 мг= 90 10 -6 кг r=1 см= 0,01м
Т2:Т1= 3 Q =?
Решение: На подвешенный шарик первоначально действуют две силы: сила тяжести Р, направленная вертикально вниз, и сила натяжения

22
Рисунок 3 Взаимодействие зарядов
нити Т1, направленная вдоль нити вверх. Шарик при этом находится в равновесии и, следовательно,
T1 = P. |
(1) |
После того как к шарику был поднесен снизу отрицательный заряд, на него кроме силы тяжести Р действует сила FK направленная вниз и определяемая по закону Кулона (рисунок). В этом случае сила натяжения
T2 = 3T1 = P + FK .
Учитывая равенство (1), запишем:
3P = P + FK или 2P = FK |
(2) |
Выразив в (2) FK по закону Кулона и силу тяжести Р через массу тела m и ускорение свободного падения g, получим:
|
|
2mg = k |
Q2 |
, |
|
|
|
|
|
εr 2 |
|
|
|||
|
|
|
|
|
|
|
|
Q = |
2mgεr 2 |
, где k = |
1 |
. |
|||
|
|
||||||
k |
4πε 0 |
||||||
Вычислим
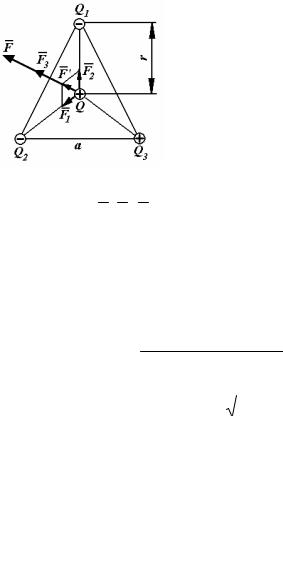
|
|
|
|
23 |
|
|
|
|
|
|
|
|
|
Q = |
2 × 9 ×10−5 |
× 9,81×1× (10−2 )2 |
|
Кл = 4,43×10-9 |
Кл. |
|
|
9 ×109 |
|
||||
|
|
|
|
|
|
|
Задача 2. В вершинах равностороннего треугольника со стороной а=20 см находятся заряды Q1 = Q2 = -10 нКл и Q3 = 20 нКл. Определить силу, действующую на заряд Q=1 нКл, расположенный в центре треугольника.
Дано:
а=20 см=0,20м
Q1=Q2 = -10 нКл= -10 -9 Кл Q3 = 20 нКл= 20 10-9 Кл
F=?
Решение: На заряд Q, расположенный в центре треугольника,
действуют три силы: F1, F2 , F3 (рисунок). Так как заряды Qt и Q2 |
равны и |
|||||||
находятся на одинаковых расстояниях от заряда Q,, |
|
|||||||
то F1 = F2 , |
(1) |
|||||||
где F1 – сила, действующая на заряд Q |
со стороны заряда Q1; F2 |
– сила, |
||||||
действующая на заряд Q со стороны заряда Q2. |
|
|||||||
Результирующая этих сил |
|
|
|
|
||||
|
|
' = |
|
+ |
|
|
|
|
F |
F |
F |
|
|||||
1 |
2 |
|
||||||
иеезначение
F ¢ = 
 F12 + F22 - 2F1F2 cosα
F12 + F22 - 2F1F2 cosα
или, учитывая (1),
F ¢ = F1 |
|
|
. |
|
2(1 - cosα ) |
(2) |
|||
|
|
|
|
|
Рисунок 4 Взаимодействие 4-х зарядов

|
|
|
|
|
24 |
|
|
|||||||||
Кроме этой силы заряд Q испытывает действие силы F3 со стороны |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
заряда Qз. Искомую |
силу |
F |
, действующую на заряд Q, найдем как |
|||||||||||||
результирующую сил |
|
¢, |
|
|
|
|
|
|
|
|
||||||
F |
F3 : F = F ¢ + F3. |
|||||||||||||||
Так как |
|
¢, |
|
|
|
|||||||||||
F |
F3 |
направлены по одной прямей и в одну сторону, то это |
||||||||||||||
векторное равенство можно заменить скалярным: F=Fэ'+FS или, учитывая (2),
F = F1 
 2(1 - cosα ) + F3.
2(1 - cosα ) + F3.
Выразив здесь F1 и F3 по закону Кулона, получим
|
Q1Q |
|
|
Q3Q |
|||
F = k |
2(1 - cosα ) + k |
||||||
|
|
|
. |
||||
εr 2 |
εr 2 |
||||||
Изрисунка следует, что |
|
|
|
|
|||
r = |
|
|
a |
|
= |
2a |
= |
a |
. |
||
|
|
|
|
|
|
|
|
||||
|
|
2 cosα / 2 |
2 3 |
|
3 |
|
|||||
С учетом этого формула (3) примет вид |
|
|
|
||||||||
|
F = |
3kQ |
(Q + Q ). |
|
|
|
|||||
|
εa2 |
|
|
|
|||||||
|
|
|
1 |
3 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||
Подставим числовые значения в (4):
(3)
(4)
F = |
3 × 9 ×10−9 |
(10−8 + 2 ×10−8 )H = 2,02 ×10−5 H |
|
1× 4 ×10−2 |
|||
|
|
Задача 3. Электрическое поле создано в вакууме двумя точечными зарядами Q1=2 нКл и Q2= -3 нКл. Расстояние между зарядами d=20 см. Определить напряженность и потенциал электрического поля, в точке, находящейся на расстоянии r1=15 см от первого и г2=10 см от второго заряда (рисунок).
Дано:
Q1=2 нКл=2×10-9Кл;
Q2= -3 нКл = - 3×10-9Кл; d=20 см= 0,20м;
r1=15 см=0,15м; г2=10 см=0,10м.
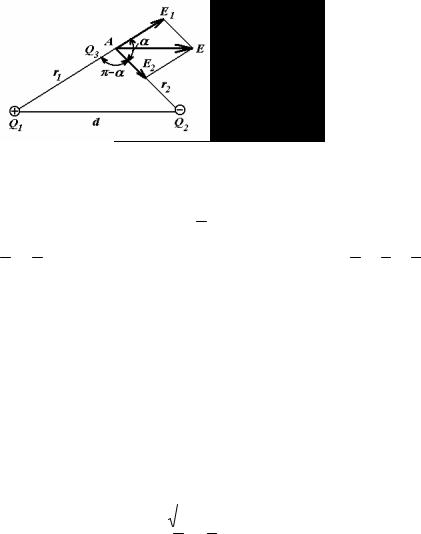
25
Рисунок 5 Напряженность электростатического поля, создаваемой системой зарядов
Решение: Согласно принципу суперпозиции электрических полей каждый заряд создает поле независимо от присутствия в пространстве других
зарядов. Поэтому напряженность E результирующего электрического поля в искомой точке может быть найдена как геометрическая сумма напряженностей
E1 и E2 полей, создаваемых каждым зарядом в отдельности: E = E1 + E2 .
Напряженности электрических полей, создаваемых в вакууме: первым зарядом
|
|
|
|
|
|
E = |
1 |
|
|
|
Q1 |
, |
|
|
(1) |
|||||
|
|
|
|
|
|
4πε |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
r 2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
|
|
|
|
|
|||
вторым зарядом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
E2 = |
1 |
|
|
|
|
Q1 |
. |
|
|
(2) |
||||
|
|
|
|
|
|
|
4πε |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
0 |
|
r |
2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
Вектор |
E1 направлен по прямой, соединяющей заряд Q1 и точку А, от |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
заряда Q1, так как он положителен; |
|
вектор |
|
E |
2 направлен по |
прямой, |
||||||||||||||
соединяющей заряд Q2 и точку А, к заряду Q2, так как этот заряд отрицателен. |
||||||||||||||||||||
Значение вектора |
E |
найдем по теореме косинусов |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
E = |
|
|
|
|
|
, |
|
|||||||||
|
|
|
|
E 2 |
+ E 2 |
+ 2E E |
2 |
cosα |
(3) |
|||||||||||
1 |
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||
где α - угол между векторами E1 и E2 . Из треугольника со сторонами r1, r2 и d найдем
cosα = |
d 2 |
− r 2 |
− r 2 |
|
|
|
1 |
2 |
. |
(4) |
|
|
2r1 r2 |
|
|||
|
|
|
|
|
|
Подставляя выражение Е1 из (1), Е2 из (2) в (3), получим

|
|
|
|
|
26 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
E = |
1 |
|
|
Q2 |
+ |
Q2 |
+ |
2Q Q |
cosα . |
|
|||
|
|
1 |
2 |
|
1 |
2 |
(5) |
||||||
4πε |
0 |
|
r 4 |
r 4 |
r 2r 2 |
|
|||||||
|
|
1 |
|
2 |
|
1 |
2 |
|
|
|
|
||
Потенциал в искомой точке А определяется алгебраической сумой потенциалов, созданных в данной точке зарядами Q1 и Q2:
ϕ = ϕ1 + ϕ2 . |
(6) |
Потенциал в точке А поля, созданного в вакууме точечным зарядом, определяется по формуле:
ϕ = |
1 |
|
Q |
. |
(7) |
|
|
||||
4πε 0 |
|
r |
|
||
Потенциал j1 является положительным, так как поле создано положительным зарядом Q1, потенциал j2 является отрицательным , так как поле создано отрицательным зарядом Q2.
Вычислим значение cosa по (4):
α = 0,22 - 0,152 - 0,12 =
cos 0,25. 2 × 0,15 × 0,1
Подставив числовые значения величин в формулу (5), найдем Е:
|
|
|
|
|
|
|
|
|
|
|
|
|
E = 9 ×10 |
9 (2 ×10−9 )2 |
+ |
(3 ×10 |
−9 )2 |
+ |
2 × 2 ×10−9 × 3 ×10 |
−9 × 0,25 |
В/м |
||||
|
(0,15) |
4 |
(0,1)4 |
(0,15)2 |
(0,1)2 |
|||||||
|
|
|
|
|||||||||
= 9 ×102 
 11,1 В/м=3×103 В/м.
11,1 В/м=3×103 В/м.
|
Подставив числовые значения величин в формулу (7), определим: |
||||
ϕ1 |
= 9 ×109 × |
|
2 ×10−9 |
= 120B ; |
|
|
|
||||
|
15 ×10−2 |
||||
ϕ2 |
= 9 ×109 × |
(-3 ×10−9 ) |
= -270B. |
||
|
|||||
|
|
|
10 ×10−2 |
||
Потенциал результирующего поля в точке А получим, подставив в формулу (6) числовые значения потенциалов j1 и j2 с учетом их знаков:
j=120 В – 270 В= - 150В.
Задача 4. Определите ток короткого замыкания IКЗ для источника ЭДС, если полезная мощность Р1 при токе в цепи I1=5 А равна 300 Вт, а при токе I2=1А – полезная мощность Р2=100 Вт.
Дано: I1=5 А
27
Р1=300 Вт
I2=1А Р2=100 Вт
IКЗ-?
Решение: Ток короткого замыкания – характеристика ЭДС
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
|
|
|
= |
Е |
, |
|
|
|
|
|
|
|
|
(1) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
КЗ |
r |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где Е - ЭДС источника, |
|
r – его |
|
внутреннее |
|
|
сопротивление. |
Полезная |
|||||||||||||||||||||||||||||||||
мощность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P=IU, |
|
|
|
|
|
|
|
|
|
(2) |
||||||||
где U – падение напряжения на внешнем сопротивлении или напряжение на |
|||||||||||||||||||||||||||||||||||||||||
зажимах источника. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
Падения напряжения на зажимах источника в первом и втором случаях |
||||||||||||||||||||||||||||||||||||||
|
|
|
= Е − I r = |
P |
|
|
|
|
|
|
|
= Е − I |
|
r = |
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
U |
1 |
1 |
и |
U |
2 |
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
|
I1 |
|
|
|
|
|
|
|
|
|
I1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
(учли формулу (2) ), откуда, вычитывая второе уравнение из первого, |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
_ |
P |
= (Е − I r) − (Е − I |
|
r) |
= (I |
|
− I )r . |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
2 |
2 |
(2) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I2 |
|
I2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Внутреннее сопротивление |
|
|
|
|
|
|
|
|
|
− P I |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r = |
P I |
2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
1 |
|
|
. |
|
|
(3) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1I2 (I2 − I1 ) |
|
|
|
|||||||||||||||
ЭДС источника |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− P I |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Е = U |
|
+ I r = |
|
P |
|
|
+ |
|
P I |
2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
2 1 |
|
(4) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
− I1 ) |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
I1 |
|
|
|
|
I2 (I2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
Подставив выражения (3) и (4) в формулу (1), найдем искомый ток |
|||||||||||||||||||||||||||||||||||||
короткого замыкания |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
= |
P I |
2 |
(I |
2 |
− I ) |
+ I . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
I |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
КЗ |
|
|
|
− P I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
P I |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ответ: IКЗ=11 А.
Задача 5. Какова скорость обращения электрона вокруг протона в атоме водорода, если орбиту электрона считать круговой с радиусом r =0,53×10-8 см ? Дано:
r = 0,53×10-8 см =0,53 ×10 -10 м; e = 1,6×10-19 Кл;
e=1;

28
e0=8,85×10-12 Ф/м; m = 9,1×10-31 кг;
v-?
Решение: При обращении электрона по круговой орбите центростремительной силой является сила электрического притяжения электрона и протона, т. е. справедливо равенство
Fцс = Fk . |
(1) |
Центростремительная сила определяется по формуле
F = mv 2 , (2)
цс |
r |
|
где m - масса электрона, движущегося по окружности; v - скорость обращения электрона; r - радиус орбиты..
Сила FK взаимодействия зарядов согласно закону Кулона выразится формулой
FK = |
Q1Q2 |
, |
(3) |
|
4πε εr 2 |
||||
|
|
|
||
|
0 |
|
|
где Q1 и Q2 - абсолютные значения зарядов;e - относительная диэлектрическая проницаемость; eо - электрическая постоянная.
Подставляя в (1) выражения Fцс из (2) и FK из (3), а также учитывая, что заряд протона и электрона, обозначаемый буквой е, одинаков, получаем
mv2 |
= |
e2 |
|
|
|
. |
|
r |
4πε 0 εr 2 |
||
Из этого выражения находим скоростьобращения электрона:
v = |
|
e |
|
||
|
|
|
. |
(4) |
|
|
|
|
|||
|
|
4πε |
0εmr |
|
|
Подставляя числовые значения величин в формулу (4) и вычислим скорость: v= 2,2×106 м/с.
Задача 6. Электрон прошел ускоряющую разность потенциалов U=800 В. Определить скорость, приобретенную электроном.
Дано: U=800 В;
е=1,60×10-19 Кл; m=9,11×10-31 кг. v-?

29
Решение: По закону сохранения энергии, кинетическая энергия Т, приобретенная зарядом, равна работе А, совершаемой электрическим полем при перемещении этого заряда:
Т=А |
(1) |
Работа сил электрического поля при перемещении заряда (в нашем |
|
случае электрона) |
|
A = eU, |
(2) |
где е - заряд электрона. |
|
Кинетическая энергия электрона |
|
|
|
|
T = |
mv2 |
, |
(3) |
|
|
|
|
|||
|
|
|
2 |
|
|
|
где m - масса электрона; v - его скорость. |
|
|
|
|
||
Подставив в (1) выражения T и A из (2) и (3), получим |
|
|||||
|
mv2 |
|
= eU , |
|
|
|
2 |
|
|
|
|||
|
|
|
|
|
||
откуда |
|
|
|
|
||
v = |
2eU |
. |
(4) |
|
m
Подставим числовые значения e,U и m в (4):
v = |
|
2 ×1,6 ×10−19 |
× 800 |
|
м/с=1,68×107 м/с. |
9,11×10−31 |
|
||||
|
|
|
|
||
Задача 7. Электромотор приводится в движение от сети напряжением U= 120 В. Сила тока, проходящего через обмотку якоря мотора при его работе I=10 А. Активное сопротивление мотора r=3 Ом. Определить мощность, потребляемую мотором, и его коэффициент полезного действия h.
Дано: U= 120 В;
I=10 А; r=3 Ом;
N1=?; h=?
Решение: Мощность, потребляемая мотором, определяется по
формуле |
|
N1 = IU = 120 ×10 = 1200Вт. |
(1) |
Коэффициент полезного действия мотора

30
|
|
|
|
η = |
N |
|
(2) |
|
|
|
|
|
N1 |
||||
|
|
|
|
|
|
|
||
где N - полезная мощность. Но |
|
|
|
|
|
|||
|
|
|
|
|
N = N1 - N2 , |
(3) |
||
где N2=l2r-— мощность, расходуемая на нагревание обмоток мотора. |
|
|||||||
Подставляя в (2) выражения для N1, N и N2 получим |
|
|||||||
η = |
U - Ir |
= |
120 -10 × 3 |
= 0,75 = 75%. |
(4) |
|||
|
|
|||||||
|
U |
120 |
|
|
|
|
||
Задача 8. В однородное магнитное поле с индукцией В=1 Тл вносится вольфрамовый стержень. Магнитная проницаемость вольфрама μ=1,0176. Определите магнитную индукцию В′ поля, создаваемого молекулярными токами.
Дано: В=1 Тл;
μ=1,0176; В′-?
Решение: Магнитная индукция поля молекулярных токов
В′=μ0J, |
(1) |
где μ0 – магнитная постоянная; J – намагниченность вольфрамового стержня. |
|
Связь между намагниченностью и напряженностью магнитного |
поля |
J=χH, |
(2) |
где магнитная восприимчивость χ и магнитная проницаемость вещества связаны соотношением:
χ=μ-1. |
(3) |
Из формулы В=μ0μН получаем |
|
B
H = |
|
. |
(4) |
μ0 μ |
Учитывая формулы (3) и (4), выражение (2) можем записать в виде
= μ -1
J μ0 μ B .
Подставив его в формулу (1), найдем искомую магнитную индукцию молекулярных токов:
В′= μ − 1 B = 17,3 ×10−3 Тл. .
μ
