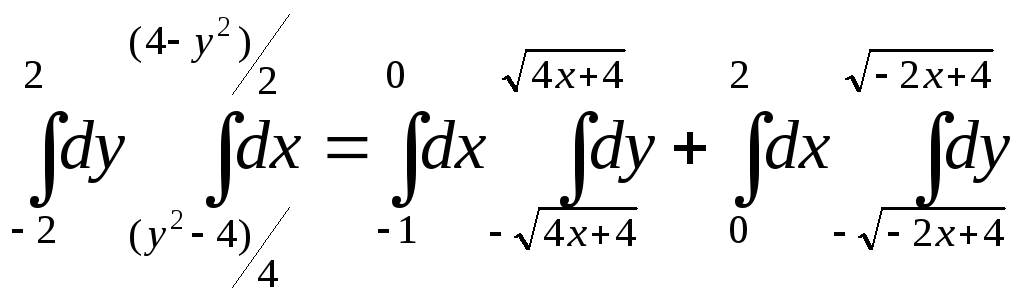- •Введение
- •Таким образом, студент, имеющий шифр 1235 должен решать задачу №8 в первом задании, №11 – во втором, №14 – в третьем, №17 – в четвертом.
- •1 Дифференциальные уравнения, их порядок, общий и частные интегралы
- •1.2 Дифференциальные уравнения второго порядка
- •Числовые ряды
- •2.1 Знакоположительные ряды
- •2.2 Знакопеременные ряды
- •2.3 Функциональные ряды
- •Варианты индивидуальных заданий
- •1. . 2..
- •Экстремум функции нескольких переменных
- •Градиент. Производная по направлению
- •5 Двойные интегралы
- •5.1 Основные понятия и определения
- •5.2 Основные свойства двойного интеграла
- •6 Элементы теории вероятностей
- •6.1 Случайные величины
- •6.1.1 Дискретные случайные величины
- •6.1.2 Числовые характеристики дискретной случайной величины
- •6.1.3 Непрерывные случайные величины
- •1) При;
- •2) При.
- •7 Варианты заданий
- •Библиографический список
Градиент. Производная по направлению
Скалярным полем
называется плоская или пространственная
область, с каждой точкой
![]() которой
связано определенное значение некоторой
физической величины
которой
связано определенное значение некоторой
физической величины![]() .
Задание поля скалярной величины
.
Задание поля скалярной величины![]() равносильно
заданию скалярной (числовой) функции
равносильно
заданию скалярной (числовой) функции![]() .
.
Линией уровня
скалярного поля называется совокупность
точек плоскости, в которых функция
этого поля имеет одинаковые значения
(![]() ,
где
,
где![]() ).
).
Градиентом
функции
![]() называется
вектор
называется
вектор
![]()
![]() =
=![]() .
.
Направление
вектора
![]()
![]() в
каждой точке
в
каждой точке![]() совпадает
с направлением нормали к поверхности
(линии) уровня, проходящей через эту
точку.
совпадает
с направлением нормали к поверхности
(линии) уровня, проходящей через эту
точку.
Производная
функции
![]() в точке
в точке![]() в направлении вектора
в направлении вектора![]() ,
образующего с осями координат углы
,
образующего с осями координат углы![]() и
и![]() ,
вычисляется по формуле
,
вычисляется по формуле
![]()
Пример 15.
Найти градиент и производную функции
![]() в
точке М(3,4)
в направлении
вектора l,
составляющего угол
в
точке М(3,4)
в направлении
вектора l,
составляющего угол
![]() с положительным направлением осиОх.
с положительным направлением осиОх.
Решение. Найдем частные производные функции в точке М:
![]() .
.
Тогда градиент
будет равен:
![]() .
.
Найдем направляющие
косинусы:
![]() .
Тогда производная по направлению будет
равна
.
Тогда производная по направлению будет
равна
![]()
![]()
![]()
5 Двойные интегралы
5.1 Основные понятия и определения
Пусть в замкнутой
области
![]() плоскости
плоскости![]() задана непрерывная функция
задана непрерывная функция![]() .Разобьём
область
.Разобьём
область![]() наn
«элементарных областей»
наn
«элементарных областей»
![]()
![]() ,
площади которых обозначим через
,
площади которых обозначим через![]() ,
а диаметры (наибольшее расстояние между
точками области) через
,
а диаметры (наибольшее расстояние между
точками области) через
![]() .
.
В каждой области
![]() выберем произвольную точку
выберем произвольную точку![]() ,
умножим значение
,
умножим значение![]() функции в этой точки на
функции в этой точки на![]() и составим сумму всех таких произведений:
и составим сумму всех таких произведений:
![]()
Эта сумма называется
функции
![]() в области
в области![]() .
.
Если существует
предел интегральной суммы, не зависящий
от способа разбиения области
![]() на части и выбора точек в них, то он
называется двойным интегралом от
функции
на части и выбора точек в них, то он
называется двойным интегралом от
функции![]() по области
по области![]() и обозначается
и обозначается![]()
Таким образом, двойной интеграл определяется равенством
![]()
![]()
В этом случае
функция
![]() называется
интегрируемой
в области
называется
интегрируемой
в области
![]() ;
;![]() -
область интегрирования;
-
область интегрирования;![]() и
и![]() - переменные интегрирования;
- переменные интегрирования;
![]() или
или
![]() - элемент площади.
- элемент площади.
5.2 Основные свойства двойного интеграла
1.
![]()
2.
![]()
3. Если область
![]() разбить линией на две области
разбить линией на две области![]() и
и![]() ,
то
,
то
![]()
![]()
4.Если в области
![]() имеет место неравенство
имеет место неравенство![]() ,
то и
,
то и![]() .
Если в области
.
Если в области![]() функции
функции![]() то и
то и![]()
![]() .
.
5. Если подынтегральная
функция
![]() ,
то двойной интеграл численно равен
площади области интегрирования:
,
то двойной интеграл численно равен
площади области интегрирования:
![]() .
.
6. Если функция
![]() непрерывна в замкнутой области
непрерывна в замкнутой области![]() ,
площадь которойS,
то
,
площадь которойS,
то
![]()
![]() ,
где
,
где
![]() и
и![]() -
соответственно наименьшее и наибольшее
значение подынтегральной функции в
области
-
соответственно наименьшее и наибольшее
значение подынтегральной функции в
области![]() .
.
7. Если функция
![]() непрерывна в замкнутой области
непрерывна в замкнутой области![]() ,
площадь которойS,
то в этой области существует такая
точка
,
площадь которойS,
то в этой области существует такая
точка
![]() ,
что
,
что
![]()
Величину
![]() называют
средним
значением функции
называют
средним
значением функции
![]() в области
в области![]() .
.
8. Координаты центра тяжести однородной пластинки можно вычислить по формулам
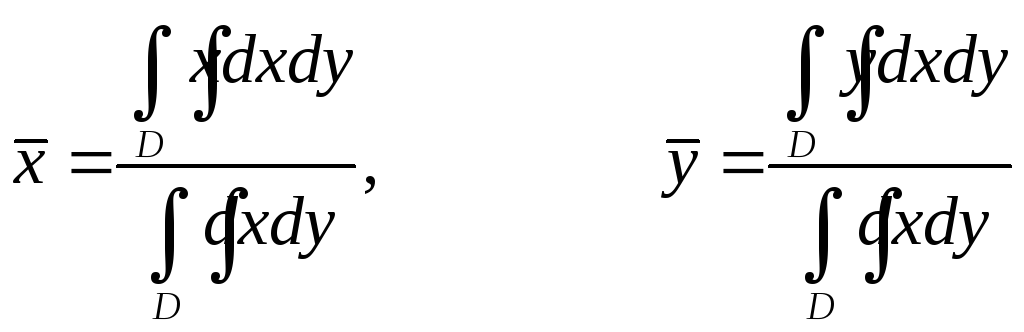 ,
,
Пример 16.
Найти координаты центра тяжести фигуры,
ограниченной линиями
![]() .
.
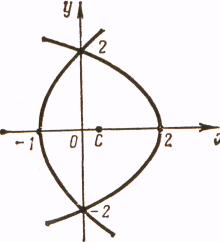
Рис.1
Решение.
Так как фигура симметрична относительно
оси
![]() ,
то
,
то![]() .
Остается найти
.
Остается найти![]() .
Найдем площадь фигуры:
.
Найдем площадь фигуры:
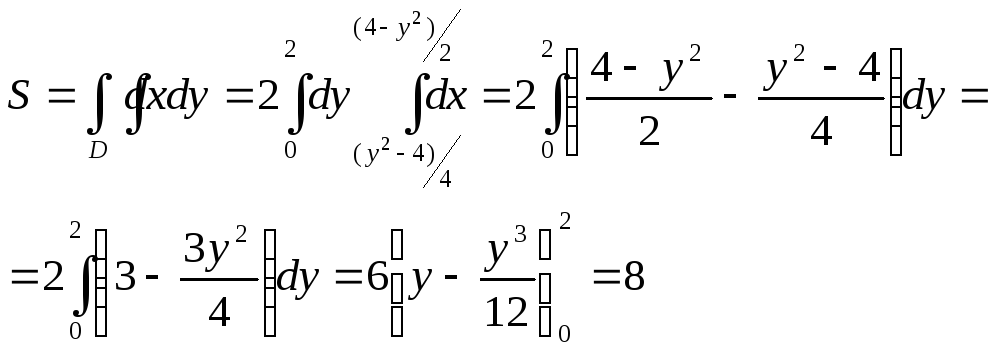
Тогда
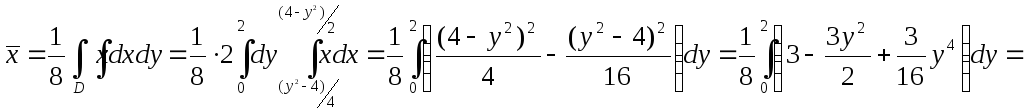
![]() .
.
Пример 17. Изменить порядок интегрирования в двойном интеграле
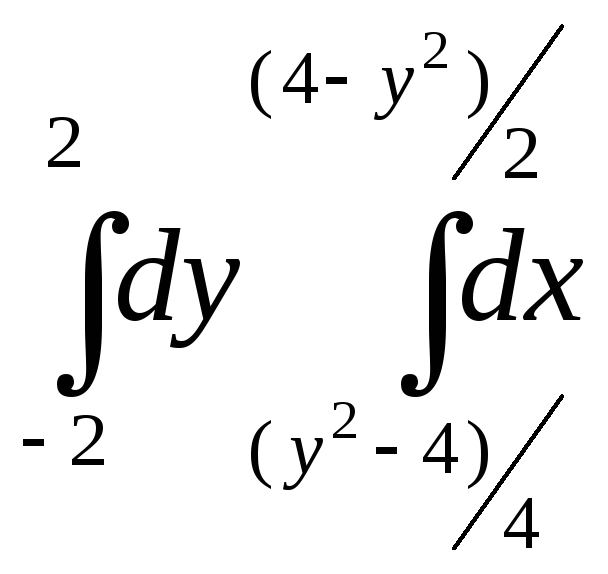 .
.
Решение.
Область интегрирования представляет
собой фигуру, изображенную на рис. 1.
Для изменения порядка интегрирования
разобьем область на две части:
![]() и
и![]() .
Тогда исходный интеграл разбивается
на сумму двух интегралов:
.
Тогда исходный интеграл разбивается
на сумму двух интегралов: