Сила тока при установившихся колебаниях: |
|
|
||||||||||||||||||||
I |
|
t |
|
|
dq |
q |
sin |
|
t |
|
|
I |
|
cos |
|
|
||||||
|
|
|
0 |
t |
|
|
||||||||||||||||
|
|
|
dt |
|
0 |
|
|
|
|
|
|
|
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
I0 |
cos t |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Амплитуда силы тока: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
I0 |
q0 |
|
|
|
U0 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
R2 L |
1 |
|
|
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тангенс сдвига фаз между током и приложенным |
|
|||||||||||||||||||||
напряжением: |
|
|
|
|
|
|
|
|
L 1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
tg tg |
|
|
|
|
C |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
Резонансная частота для заряда и напряжения на |
|
|
|||||||||
конденсаторе: |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 2 |
|
1 |
|
R2 |
|
|
||
|
|
2 |
0 |
||||||||
qрез |
UC рез |
|
0 |
|
|
|
LC |
|
|
||
|
|
|
|
|
|
|
|
2L |
|
|
|
Для тока: |
|
|
|
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|||||
|
|
|
рез |
|
0 |
LC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
При малом затухании |
2 02 |
|
|
|
|
|
|
||||
|
UC0 рез |
|
1 |
|
1 |
L |
Q |
|
|
|
|
|
|
R |
|
|
|
|
|
|
|||
|
UСR |
C |
|
|
|
|
|
|
|
||
|
0 |
|
0 |
|
|
|
|
|
|
|
|
- добротность показывает, во сколько раз напряжение на |
|
||||||||||
конденсаторе при резонансе может превысить приложенное |
|||||||||||
напряжение. |
|
|
|
|
|
|
|
|
|
|
|
Резонансные кривые колебательного контура при различных добротностях
Q1 > Q2 > Q3
qст |
U0 |
|
- статическое значение заряда при |
|
L 02 |
||||
|
постоянной ЭДС (ω = 0) |
|||
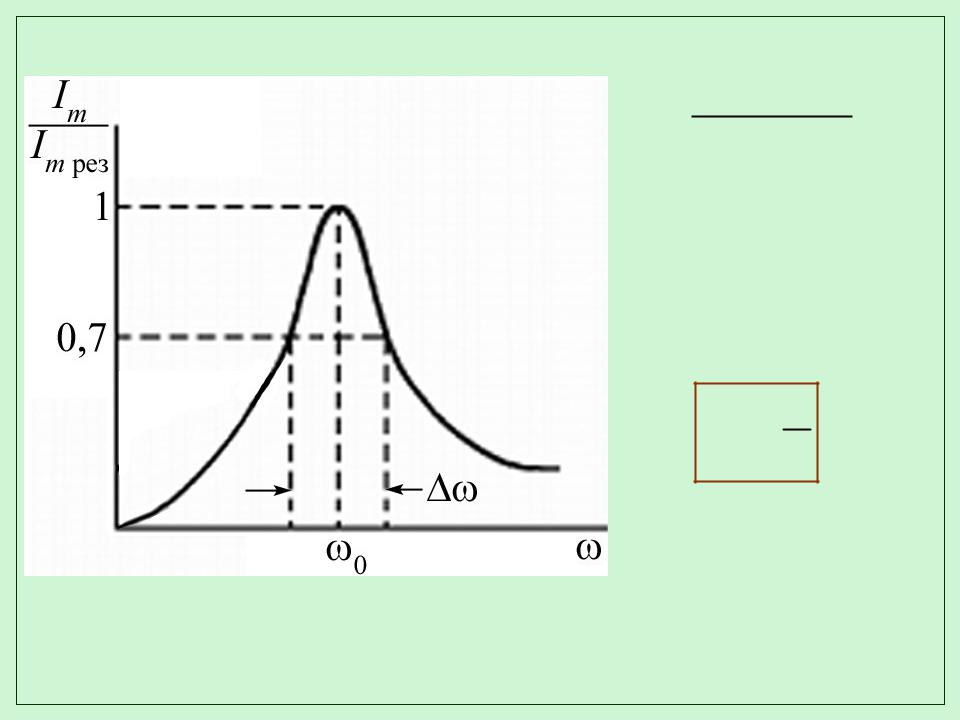
- ширина
резонансной
кривой (граничные значения – частоты, при которых энергия колебаний вдвое меньше энергии в максимуме)
10 Q
- чем выше добротность контура, тем уже резонансная кривая
2. Установление колебаний. Биения
Если у колебательной системы большая добротность (τ >> T), процесс установления колебаний носит затяжной характер:
В предельном случае ( = 0)
и начальных условиях |
х(0) = 0, |
v(0) = 0
решение уравнения имеет вид
x t |
|
|
F0 / m |
|
|
cos t cos 0t |
|
|
|||
|
|
2 |
2 |
|
|
|
|
||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
2F0 / m |
|
|
sin 0 |
t sin |
0 |
t |
|
|
|
|
|
|
|
|||||||
|
|
|
2 |
02 |
|
2 |
|
2 |
|
|
|
A t sin |
|
0 t |
|
|
|
|
|||||
|
|
|
|
|
2 |
|
|
|
|
||
где |
|
|
|
|
|
|
|
|
A t |
|
2F0 / m |
|
sin |
0 |
t |
||
|
|
|
||||||
|
|
|
|
|||||
|
2 02 |
2 |
||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Полуразность частот: |
1 |
0 |
|
|||||
|
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
|
При 0 частота колебания близка к собственной:
0 0 0
2
и амплитуда колебаний будет медленно и периодически изменяться со временем - биение.
Период повторения биений: |
|
|
|
|
T |
|
|
||
|
||||
|
|
|||
|
|
|||
В случае резонанса ( |
|
|
|
0): |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
x |
t |
|
|
2F0 / m |
sin t sin t |
|
|
|
2F0 |
/ m |
sin |
t |
sin |
t |
|
|||||
|
|
|
0 0 |
|||||||||||||||||
|
|
|
2 02 |
0 |
|
|
|
|
|
|
0 |
|
||||||||
|
|
|
|
2F0 / m |
sin t sin |
t |
F0 / m t sin t |
sin |
t |
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
2 2 |
|
0 |
|
2 |
t |
|
0 |
|
|
|
||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
F0 |
t sin t |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2m 0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
x |
t |
|
|
F0 |
t sin t |
|
2m |
||||||
|
|
|
0 |
|||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
Амплитуда колебаний:
A t |
F0 |
t |
2m |
||
|
0 |
|
- линейное возрастание амплитуды колебаний при резонансе в
отсутствие сил трения или сопротивления в цепи
- при наличии сил трения рост амплитуды будет остановлен, колебания перейдут в колебания постоянной амплитуды