Сегодня: Thursday, July 4, 2019 |
Лекция 3 |
Колебания
Содержание лекции:
Вынужденные колебания
•механические
•электрические
Установление колебаний. Биения
1.1. Вынужденные механические колебания 
Пусть вынуждающая сила изменяется по гармоническому закону: F = F0 cos ωt.
Запишем второй закон Ньютона для колеблющейся системы: mx& kx rx& F0 cos t
или |
|
|
|
|
|
|
F0 |
|
&x 2 x& 2 x f |
0 |
cos t, |
f |
0 |
|
|||
|
||||||||
|
|
|||||||
|
0 |
|
|
|
m |
|||
|
|
|
|
|
|
|
- неоднородное ДУ, описывающее вынужденные колебания.
Его решение складывается из:
1)общего решения однородного ДУ (получено ранее);
2)частного решения неоднородного ДУ;
Получим его с помощью метода векторных диаграмм:
Предположим, что оно имеет вид |
|
x Acos t |
Дифференцируя по времени, получаем:
x& Asin |
|
t |
|
Acos |
|
|
|
|
|||||
|
|
t |
2 |
|||
|
|
|
|
|
|
&x 2 Acos t 2 Acos t
При подстановке в ДУ получаем:
2 Acos t |
|
||
2 Acos |
|
|
|
t |
|
|
|
|
|
2 |
|
|
|
|
|
02 Acos t f0 |
cos t |
||
Сумма этих трех колебаний на векторной диаграмме имеет следующий вид:
По теореме Пифагора находим квадрат гипотенузы:
02 2 2 A2 4 2 2 A2 f02
Определяем значение амплитуды:
A |
f0 |
|
|
|
F0 / m |
|
|
|||
|
2 |
|
|
|
2 |
|
|
|
||
2 |
2 |
2 |
2 |
2 |
2 |
2 |
|
2 |
||
|
|
4 |
|
|
4 |
|
||||
0 |
|
|
|
|
0 |
|
|
|
|
|
И начальную фазу вынужденных колебаний: |
|
|
||||||
|
2 |
|
- отставание по фазе от вынуждающей |
|||||
|
tg 02 2 |
силы |
|
|
|
|
||
Итак, частное решение неоднородного ДУ: |
|
|
||||||
|
x |
F0 |
/ m |
|
|
2 |
|
|
|
|
cos t arctg |
|
|||||
|
2 |
2 |
2 |
|
2 2 |
|
2 2 |
|
|
0 |
|
|
4 |
|
0 |
|
|
- |
не содержит произвольных констант! |
|
|
|||||
|
Амплитуда этих колебаний зависит от частоты вынуждающей |
|||||||
|
силы, при некотором значении ω наблюдается максимум |
|||||||
|
амплитуды – резонанс (соответствующая частота - |
|||||||
|
резонансная). |
|
|
|
|
|
|
|
Определим резонансные параметры:
найдем экстремум знаменателя амплитуды (минимум знаменателя
соответствует максимуму амплитуды):
2 02 2 2 8 2 0
Следовательно, резонансная частота
рез 02 2 2
Амплитуда при резонансе
Aрез |
|
F0 / m |
|
|
2 |
2 |
2 |
||
|
|
0 |
|
|
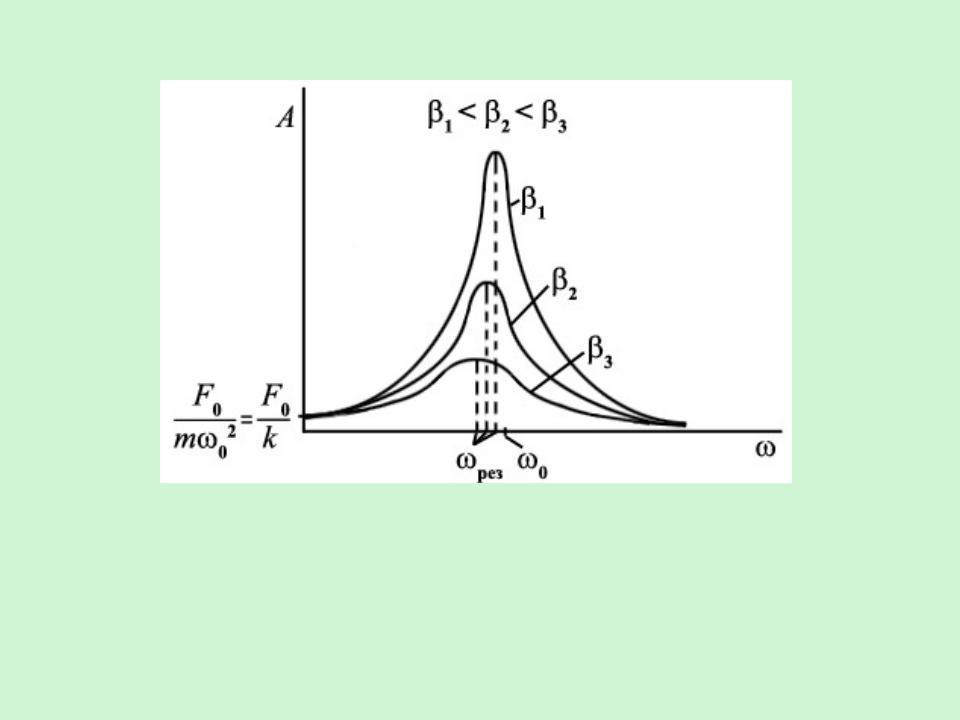
Семейство резонансных кривых
Общее решение неоднородного ДУ графически:
1 – установление колебаний, здесь превалирует общее решение однородного ДУ (далее им можно пренебречь из-за экспоненциального затухания);
2 – установившиеся колебания, описываемые частным решением неоднородного ДУ: гармонические колебания с частотой, равной частоте вынуждающей силы и амплитудой, зависящей от частоты вынуждающей силы.
1.2. Вынужденные электрические колебания
Описываются неоднородным дифференциальным уравнением:
d 2q |
2 |
dq |
2q |
U |
0 |
cos t |
|
|
|
|
|||
dt2 |
|
dt |
0 |
|
|
L |
|
|
|
|
Его решение складывается из: 1) частного решения
q t q0 cos t
где
tg |
2 |
|
|
|
|
R |
- фаза вынужденного |
|
2 |
2 |
|
1 |
|
|
|||
|
0 |
|
|
|
L |
колебания |
||
|
|
|
|
C |
||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
q0 |
|
U0 |
L |
|
U0 |
|
|
|
|
2 |
|
R2 |
1 |
2 |
|||
|
|
|
|
|
||||
|
|
02 2 |
|
4 2 2 |
|
|
||
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
- амплитуда вынужденного колебания.
2) общего решения однородного уравнения (быстро убывающего со временем).